Преподаватель – Шнейдер Елена Борисовна
1. Найдите для следующих функций MRS, MUx, Muy.
а) U=xy
б) U=x2y2
в) U=lnx+lny
2. Дана функция полезности U(X,Y)= X×Y. Является ли монотонным преобразованием функции U(X,Y)
а) функция V(X,Y)=X3×Y3+100?
б) функция V(X,Y)=X3×Y3+x?
в) функция V(X,Y)=X1/2×Y1/3?
3. Дана функция полезности потребителя U(X,Y)=X+Y.
а) Изобразить карту безразличия для предпочтений, представленных этой функцией.
б) Чему равна предельная норма замещения товара Х товаром Y?
в) Определите оптимальный набор при бюджетном ограничении 10X+5Y=20.
4. Изобразите кривые безразличия для следующих функций полезности и проверьте, выполняется ли предпосылка об убывании MRS.
а) U=3 x + y
б) U= 
в) U= 
г) U= 
д) U= 
е) U=ln x +ln y
5. Пусть функция полезности имеет вид: U(x,y)= 
.
а) Изобразите кривую безразличия при U= 10.
б) Чему равно у при х =5, U=10? Чему равно MRS в этой точке?
в) Найдите общее выражение для MRS.
6. Ежедневно ученик завтракает в школе. Он ест конфеты (x) и пьет сок (y). Его функция полезности 
.
а) Если конфета стоит 1руб., а стакан сока 2,5руб., как потратит ученик 10руб., которые мама дает ему на завтрак?
б) Если школа увеличит цену конфет до 4руб., чтобы уменьшить их потребление, как должна мама увеличить сумму на завтрак, чтобы обеспечить ученику прежний уровень полезности? Как потратит ученик деньги теперь (если можно купить часть конфеты и неполный стакан сока)?
7. Функция полезности потребителя U= , сумма, которую он намерен потратить на х и у - 300 руб.
Цена единицы х - 20 руб., а единицы у - 4 руб. Сколько он приобретет х и сколько у?
Как изменится ответ, если цена х уменьшится до 10 руб.?
8. Функция спроса на благо x задана выражением:
х(
, 
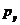)=12-2 
+ 
, где - цена блага х, 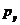- цена блага у.
а) Найти 
, если перекрестная эластичность спроса на благо х по цене блага у при 
=3 составляет 0,125.
9. Функция спроса на благо x задана выражением:
х(, 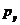)=20-4 + 
, где - цена блага х, 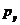- цена блага у.
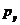а) Найти перекрестную эластичность спроса на благо х по цене блага у при =3, =0,5.
б) Являются ли блага х и у субститутами или комплементами?
10. Издержки фирмы, действующей в условиях совершенной конкуренции в краткосрочном периоде выражаются функцией c(q)= 0,1 ×q 
+ 6 ×q+ 80
где q единиц- количество выпускаемой за месяц продукции,
с(q) - общие издержки в тыс.руб.
а) Найти равновесный выпуск и прибыль фирмы, если рыночная цена составляет р =16 руб. за ед. продукции.
б) Если правительство вводит паушальный налог Т = 3 руб. в месяц, какими будут равновесный выпуск и прибыль фирмы при прежней цене 16 руб. за ед. продукции.
11. Фирма функционирует в конкурентной отрасли. Фирма и отрасль находятся в состоянии долгосрочного равновесия. Функция издержек фирмы TC(q)= 0,5q3 -4q2 +150q
Найти равновесный выпуск фирмы. Если рыночная функция спроса Qd=500-P, определить число фирм в отрасли.
12. Кривая спроса конкурентной отрасли: Qd=1500-50P. В отрасли 50 идентичных фирм.
Функция издержек фирмы: C(q)=0,5q2-10q+200
Найти равновесную цену и равновесный выпуск фирмы.
13. Издержки фирмы, действующей в условиях совершенной конкуренции, в краткосрочном периоде выражаются функцией c(q)= 0,5 ×y + 2 ×y+ 3
где q единиц - количество выпускаемой за месяц продукции,
с(q) - общие издержки в руб.
а) Найти равновесный выпуск и прибыль фирмы, если рыночная цена составляет р =12 руб. за ед. продукции.
б) Если правительство вводит паушальный налог Т = 4 руб. в месяц, какими будут равновесный выпуск и прибыль фирмы при прежней цене 12 руб. за ед. продукции.
14. В краткосрочном периоде производственная функция конкурентной фирмы имеет вид: Q(L)= 16L -L2, где L - количество используемого труда. Цена выпускаемой продукции - 2.
Найдите выражение для кривой спроса фирмы на труд.
Если заработная плата равна 12, какое количество труда наймет фирма.
15. Рыночный спрос описывается уравнением P=77-3Q. На рынке представлены 2 фирмы, заключившие картельное соглашение. Общие издержки фирм равны соответственно TC1=2q12 и TC2=q22. Определить, какие квоты установит картель и какой будет цена. Сколько будет стремиться производить фирма 1, если она полагает, что ее конкурент не будет нарушать картельное соглашение?
16. Найдите равновесие в модели дуополии Курно, если издержки фирм выражаются функциями TC1= 12q1 и TC2=3q22, а рыночный спрос задан уравнением P=168-6Q.
17. Предприниматель решает вопрос об инвестициях в оборудование, рассчитанное на 2 года и полностью изнашивающееся за этот период. Ежегодный доход, который он ожидает получать от использования этого оборудования составляет 200 млн.руб. Какова максимальная цена по которой он приобретет данное оборудование, если рыночная ставка процента составляет 10% годовых?
18. Предприниматель решает вопрос об инвестициях в оборудование, которое он намерен эксплуатировать 3 года. Ежегодный доход от оборудования, который он ожидает получать от использования этого оборудования составляет 100 млн.руб. и, кроме того, он рассчитывает продать оборудование после 3-х лет эксплуатации по остаточной стоимости 20 млн.руб. Какова максимальная цена по которой он приобретет данное оборудование, если рыночная ставка процента составляет 10% годовых?