Тема 3: Учет фактора времени в управлении финансами
1. Временная ценность денег
2. Наращение и дисконтирование капитала
3. Процентные ставки и методы их начисления
4. Виды денежных потоков
5. Оценка денежных потоков с неравномерными поступлениями
6. Оценка аннуитета
7. Метод депозитной книжки
1.
Любой финансовой операции и коммерческой сделки денежные суммы связаны с конкретными моментами времени. В контрактах или договорах всегда предусмотрены сроки и периодичность поступления денежных средств, поэтому прежде чем принять управленческое решение, финансовый менеджер должен сопоставить прошлые, настоящие и будущие расходы и доходы. С переходом к рынку перед финансовой службой встали новые задачи о наиболее эффективном вложении денежных средств, появились новые финансовые ресурсы (краткосрочные финансовые вложения, долевые взносы), новые варианты вложения средств, связанные с риском (ценные бумаги, недвижимость, венчурные предприятия).
Основным правилом управления финансами является – свободные денежные средства должны быть быстро вложены в наиболее эффективные инструменты для получения дополнительного дохода.
2.
Самым простым видов финансовых сделок является однократное предоставление в долг некоторой суммы К, что через определённое время Т будет возвращена большая сумма КТ. Результат этой сделки можно оценить с помощью абсолютного показателя приращения КТ – К и с помощью относительного показателя Ставки.
Кт
К Т
Ставка рассчитывается как отношение приращения исходной величины к базовой. В качестве базовой величины можно взять исходную сумму К или приращенную сумму КТ. Поэтому ставку можно рассчитать по двум формулам:
|
|
1. Темп прироста Zt=(Kt-K) / K (показываем на сколько % выросла исходная сумма К)
2. Темп снижения Dt = (Kt-K)/Kt
В финансовых расчетах Ztназывают процентной ставкой или нормой прибыли (доходности), Dt–учетной ставкой или ставкой дисконта.
При составлении прогнозных расчетов используют обе формулы в зависимости от поставленных задач.
Если заданы исходная сумма и % ставка, то такой процесс финансовых расчетов называется процессом – наращения.
Если известно ожидаемая в будущем сумма и коэффициент дисконтирования, то такой процесс в финансовых расчетах называется дисконтированием.
Пример, предприятие получило кредит в 100тыс.руб (К) с условиями возврата 140тыс.руб (Кт). Определить % и учетные ставки наращения и дисконтирования.
Zt = 140-100 / 100 = 0.4 (40%)
Dt = 140-100 /140 = 0,286 (28,6%)
Дисконтирование дохода – это приведение дохода к моменту вложения капитала. Чтобы определить сумму наращенного капитала и дополнительного дохода с учетом дисконтирования используют следующую формулу. Данная формула учитывает количество периодов вложения капитала, т.е. капитала вкладывается не на один период, а на несколько.
FV = PV*(1+n)t
FV – размер капитала к концу периода t
PV – текущая оценка капитала с позиции исходного периода
n – коэффициент дисконтирования (норма доходности или % ставка в долях.ед.)
t – фактор времени (число лет или количество оборотов капитала)
Пример, вложены деньги в банк на депозит в сумме 100тыс.руб. на 2 года. Определить величину наращенного капитала по истечении периода, если банк начисляет 10% годовых.
FV =100 000(1*0,1)2=121тыс.руб.
|
|
В зависимости от постановки задачи необходимо рассчитать стоимость первоначального капитала PVи ставку дисконта (норму прибыли n).
Получаем формулы: PV = FV / (1+n)t
Пример, банк предлагает 30% годовых, определить каким должен быть размер первоначального вклада, чтобы через 2 года, его размер достиг 10 тыс.руб.
PV = 10 000/ (1*0.3)2 = 5900руб.
n = (FV/PV)1/t – 1
Пример, инвестор желает первоначальную сумму в размере 20тыс.рубв течении 2 лет увеличить до 70тыс.руб. Какова должна быть норма доходности (% дисконта).
N = (70/20)1/2 – 1 = 0,87 или 87%
Если % начисляются несколько раз в год (реинвестирование капитала), то формула дисконтирования дохода будет такая.
FV = PV(1+n/m)tm
m- число периодов начисления в году.
Tm – число начислений за весь период вклада
Пример, вложены деньги в банк в сумме 100тыс.руб на 2 года с полугодовым начислением % под 20% годовых. Определить величину капитала по истечении срока вклада.
FV = 100 000(1+0.2/2)4=146.410руб.
Для упрощения атематических расчетов созданы специальные финансовые таблицы. В этих таблицах приведены финансовые коэффициенты, величина которых зависит от числа периодов начислений и применяемой ставки. Эти коэффициенты называются мультиплицирующий множитель.
Так предыдущие формулы можно упростить, заменив 2ой множитель на мультиплицирующий множитель для единичного платежа.
FM (r,n)
R – ставка
N–количество периодов
Процентная ставка rв финансовых таблицах соответствует длине базисного периода, т.е. если в таблице n- это количество кварталов, то ставка r– квартальная, если годы - годовая.
Решение предыдущего примера будет выглядеть следующим образом:
|
|
FV= PV*FM(r,n)
Пример, вложены деньги в банк в сумме 100тыс.руб на 2 года с полугодовым начислением % под 20% годовых. Определить величину капитала по истечении срока вклада.
FV = 100 000*FM(0,1;4)
FM (0,1;4) = 1,4641 (по таблице)
FV= 100 000*1,4641 = 146,410тыс.руб.
3.
Необходимость учета фактора времени наиболее ярко проявляется в процессе ссудно-заемных операций, предоставляя в долг денежные средства кредитор получает доход в виде суммы %. В финансовых операциях временным интервалом чаще всего является год, поэтому самым распространённым вариантом является годовая ставка.
Существует 2 схемы начисления процентов:
- схема простых процентов
- схема сложных процентов
При начислении простых процентов база, с которой начисляются % остается неизменной.
Допустим, исходный капитал равен PV, а требуемая доходность rв долях ед. Если инвестируемый капитал ежегодно увеличивается на величину PV*r, то инвестирование сделано по схеме простого %.
PV+PV*r+…+PV*r = PV (1+t*r)
Обычно схему простых % банки используют когда начисляют % по краткосрочным ссудам сос роком погашения до 1 года.
Пример, выдана ссуда 120тыс.руб на 30 дней под 26% годовых. Определить размер платежа к погашению.
PV = 120 000 (1+0.26/360) = 122,6тыс.руб
При расчете суммы простого % - S, в процессе наращения стоимости используется следующая формула
S=PV* t* r
Пример, определить сумму простого % за год при следующих условиях: первоначальная сумма вклада 100тыс.руб., ежеквартальная % ставка r – 20%
S = 100 000 * 4*0,2 = 80 000 - это наращение капитала
Множитель (1+tr) называется множителем (коэффициентом) приращения. Его значение всегда должно быть больше 1
При расчете суммы простого % в процессе дисконтирования (т.е. при расчете суммы дисконта - D) используется формула
D = FV –FV*(1/1+tr)
В этом случае настоящая стоимость денежных средств PVcучетом рассчитанной сумму дисконта определяется по формуле.
PV = FV – D
Или
PV = FV*(1 / 1+tr)
Пример, определить сумму дисконта по простому % за год при следующих условиях:
- конечная сумма вклада 1000 тыс.руб
- ставка 20% в квартал
D = 1000 -1000(1 / 1+4*0,2) = 444тыс.руб
PV = 1000 – 444 = 556 тыс.руб – мы должны вложить, чтобы получить 1000тыс.руб при имеющейся ставке в размере 20%. При этом множитель 1 / 1+ tr - называется дисконтным множителем (коэф.) суммы простых %, значение которого всегда должно быть меньше 1
При расчете суммы простого процента в процессе дисконтирования стоимости D, т.е при расчете суммы дисконта используется формула D = FV *-FV * 1/ (1+ tr).
Пример: определить сумму дисконта по простому проценту за год при следующих условиях. Конечная сумма вклада 1000 т.р., ставка 20 % в квартал.
D = 1000 – 1000 1 /(1 +4*0,2) = 444 т.р
PV = 1000 – 444 = 556 т.р.
Соответственно настоящая стоимость вклада необходимого для получения через год должна составить 556 т.р., при этом множитель 1/(1+ tr) называется дисконтным множителем суммы простых процентов значение которого всегда должно быть меньше 1.
При использовании схемы сложного % очередной годовой доход исчисляют не с исходной суммы, а суммы которая включает в себя ранее начисленные %.
В этом случае размер инвестированного капитала к концу первого года составит FV1 = PV*(1+r) к концу второго года FV 2 = PV* (1+r)2к концу 3 года - FV3 = PV* (1+r)3и к концу года t - FV = PV* (1+r)t
Формула сложного % одна из базовых формул при финансовых расчетах. Данная формула аналогична формуле дисконтированного дохода.
При расчете будущей суммы вклада FVв процессе его наращения по сложным процентам используется формула
FV =PV* (1+r)t
Сумма % рассчитанного в процессе наращения s
Sc = FV – PV
Пример, определить будущую стоимость вклада и сумму сложного % за весь период инвестирования при следующих условиях: PV-1000руб, r-20%, t- 1 год
FV = 1000*(1+0,2)4=2077руб.
Sc = 2077 – 1000 = 1077 руб. – сумма %
При расчете настоящей стоимости денежных средств в процессе дисконтирования по сложным % используется след. Формула
Dc = FV – PV
Пример, необходимо определить настоящую стоимость денежных средств и сумму дисконта по сложным % за год при след.условиях: FV- 1000тыс.руб.r-20% в квартал
PV = 1000 / (1+0,2)4 = 482тыс.руб
Dc = 1000 – 482 = 518 тыс.руб.
Методический инструментарий оценки стоимости денег по сложным % использует такие показатели как средняя % ставка (r), длительность общего периода платежа (t), определение эффективной % ставки в процессе наращения стоимости денежных средств.
При определении средней процентной ставки используемой в расчетах стоимости денежных средств по сложным процентам применяется формула:
r= (FV/PV)1/t - 1
Пример: Определить годовую ставку доходности облигации при следующих условиях – номинал облигации подлежащий погашению через 3 года составляет 1000 тыс. руб. Цена по которой облигации реализуется в момент ее эмиссии составляет 600 тыс. руб.
r=(1000/600)1/3 – 1 = 0,186 (18,6%)
Длительность общего периода платежей выраженная количеством его интервалов в расчетах стоимости денежных средств по сложным процентам определяется путем логарифмирования по формуле:
t= (log (FV/PV)) / (log (1+r))
=4=
В результате реализации какого-либо инвестиционного проекта инвестор в течении определенного периода времени получает доходы от инвестирования. Все поступления денежных средств могут быть либо в начале, либо в конце периода.
Когда денежные поступления поступают в начале периода данный денежный поток называется потоком пренумерандо (авансовым поступлением). Поток пренумерандо имеет значение при анализе накопления денежных средств для дальнейшего их инвестирования.
Когда поступления осуществляются в конце периода данный поток называется потоком постнумерандо. Данный вид потока является более распространенным. Поток постнумерандо положен в основу методики анализа инвестиционных проектов.
Оба вида денежных потоков можно оценивать с позиции наращения и с позиции дисконтирования.
Когда денежный поток оценивается с позиции наращения решается прямая задача, а когда с позиции дисконтирования обратная задача. В том и другом случае следует предположить что происходит капитализация по схеме сложного процента.
Схема – виды денежных потоков
| Прямая задача (с позиции наращения) | Обратная задача (с позиции дисконтирования) |
| Поток постнумерандо FV pst | Поток постнуменрандо PV pst |
| Поток пренумерандо FV pre | Поток пренумерандо PV pre |
=5=
Аннуитет – равные платежи. Ситуация когда денежные поступления по годам варьируют является наиболее распространенной.
Оценка потока постнумерандо:
1. Прямая задача. Предполагает оценку с позиции будущего, т.е. на конец периода t, когда реализуется схема наращения. Представим что множество CFk это совокупность периодических денежных взносов в банк на депозит. При этом k –порядковый номер платежа. К = 1,2 …t. Какая сумма будет к концу данной операции?
Простое суммирование элементов потока CFk невозможно так как они находятся в разных временных интервалах что обуславливает их несопоставимость из за временной ценности денег. эТа несопоставимость устраняется с помощью наращения по схеме сложных процентов. Таким образом общая формула для исчисления будущей стоимости потока постнумерандо будет иметь вид:
FV pst = 
Где
R – ставка дисконтирования
T - число базисных периодов
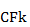- сумма платежа
K – порядковый номер платежа
Пример: Денежные взносы в банк на депозит составили в первом периоде 10 тыс. руб, во втором периоде – 15 тыс.руб, в третьем периоде – 12 тыс.руб. Определить наращенную сумму к концу операции. Ставка дисконтирования 20 %
FV pst = 10 ((1+0,2) 3-1 + 15 * (1 +0,2) 3-2 + 12 (1+0,2) 3-3 = 44,4
2. Обратная задача. Подразумевает оценку с позиции текущего момента, т.е. все элементы ожидаемого денежного потока сводятся к началу финансовой операции. Представим себе что множество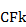 
это совокупность регулярных доходов по ценной бумаге, которую инвестору предлагают купить. Инвестор хочет понять сколько он готов заплатить за возможность обладания данным денежным потоком и какова величина вознаграждения за единовременное отвлечение своих средств связанное с покупкой этой ценной бумаги.
Простое суммирование элементов денежного потока как и в предыдущем случае невозможно, так как во времени они не сопоставимы. Эта несопоставимость устраняется с помощью дисконтирования по схеме сложных процентов. Расчет дисконтированной стоимости данного потока сводиться к приведению каждого его элемента к началу финансовой операции т.е. делению на множитель 
соответствующей степени и дальнейшему их суммированию. Таким образом общая формула для исчисления дисконтированной стоимости потока постнумерандо имеет следующий вид:
PV pst =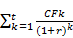 
Если использовать дисконтирующий множитель 1/(1+r)k и обозначить его = FM 2 (r;k), таким образом получаем
PV pst = 
Пример: Рассчитать дисконтированную стоимость денежного потока постнумерандо: 12, 15, 9, 25 млн.руб. это совокупность регулярных доходов по ценной бумаге, ставка дисконтирования 12%.
| Год | Денежный поток, млн.руб. | Дисконтирующий множитель, FM2(0,12;k) | Дисконтированный поток, млн.руб. |
| К=1 | 12 | 0,8929 | 10,71 |
| К=2 | 15 | 0,7972 | 11,96 |
| К=3 | 9 | 0,7118 | 6,41 |
| К=4 | 25 | 0,6355 | 15,87 |
| Итого: | 61 | 44,97 |
Оценка потока пренумерандо.