1. Автомобиль движется по прямой улице. На графике представлена зависимость скорости автомобиля от времени. Чему равен максимальный модуль ускорения? Ответ выразите в м/с2.
Задание 1 № 104
Решение.
На всех рассматриваемых интервалах времени скорость автомобиля меняется равномерно, следовательно ускорение на каждом интервале постоянно. Рассчитаем ускорения:
в интервале от 0 до 10 с: 
в интервале от 10 до 20 с: 
в интервале от 20 до 30 с: 
в интервале от 30 до 40 с: 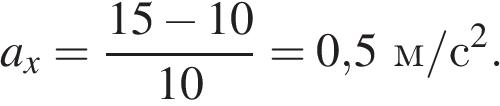
Максимальный модуль ускорения равен 2 м/с2.
Ответ: 2 м/с2.
Ответ: 2
2. Тело разгоняется на прямолинейном участке пути, при этом зависимость пройденного телом пути S от времени t имеет вид:

Чему равна скорость тела в момент времени t = 2 c при таком движении? (Ответ дайте в метрах в секунду.)
Задание 1 № 111
Решение.
При равноускоренном движении зависимость пройденного телом пути от времени в общем виде имеет вид
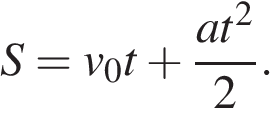
Сравнивая с выражением, данным в условии, заключаем, что оно укладывается в это общее правило, а значит тело двигалось равноускоренно. Сопоставляя конкретные члены в выражениях получаем, что начальная скорость равна 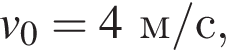 а ускорение
а ускорение 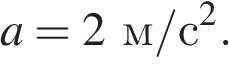 Таким образом, скорость тела в момент времени
Таким образом, скорость тела в момент времени  равна (
равна ( ):
):
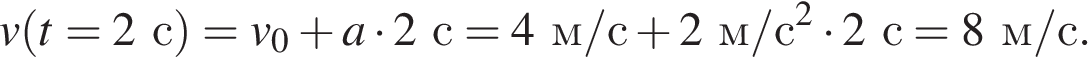
Ответ: 8
3. При прямолинейном движении зависимость координаты тела x от времени t имеет вид:

Чему равна скорость тела в момент времени t = 2 c при таком движении? (Ответ дайте в метрах в секунду.)
Задание 1 № 112
Решение.
При равноускоренном движении зависимость координаты тела  от времени в общем виде следующая:
от времени в общем виде следующая:
 .
.
Сравнивая с выражением, данным в условии, получаем, что проекция начальной скорости равна 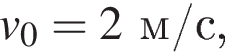 а ускорение
а ускорение 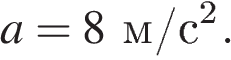 Таким образом, скорость тела в момент времени
Таким образом, скорость тела в момент времени  равна
равна
 .
.
Ответ: 18
4. Зависимость координаты x тела от времени t имеет вид:
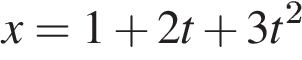 .
.
Чему равна проекция скорости тела на ось Ox в момент времени t = 3 с при таком движении? (Ответ дайте в метрах в секунду.)
Задание 1 № 113
Решение.
1 способ:
Проекция скорости — это производная соответствующей координаты по времени, а потому закона изменения проекции скорости со временем имеет вид:
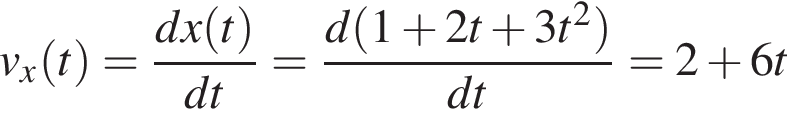 .
.
Следовательно, в момент времени 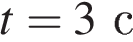 проекция скорости на
проекция скорости на
ось Ox равна:
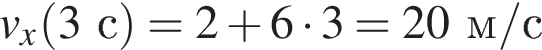 .
.
2 способ:
При равноускоренном движении зависимость координаты тела x от времени в общем виде следующая:
 .
.
Сравнивая с выражением, данным в условии, получаем, что проекция на ось Ox начальной скорости равна  а проекция ускорения равна
а проекция ускорения равна  Таким образом, проекция скорости тела на ось Ox в момент времени
Таким образом, проекция скорости тела на ось Ox в момент времени 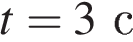 равна
равна
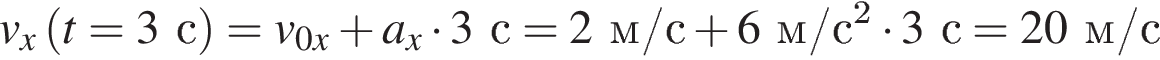 .
.
Ответ: 20
5. Зависимость координаты x тела от времени t имеет вид:
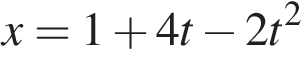 .
.
Чему равна проекция скорости тела на ось Ox в момент времени t = 1 с при таком движении? (Ответ дайте в метрах в секунду.)
Задание 1 № 114
Решение.
1 способ:
Проекция скорость есть производная от координаты по времени. Таким образом, зависимость проекции скорости тела от времени имеет вид
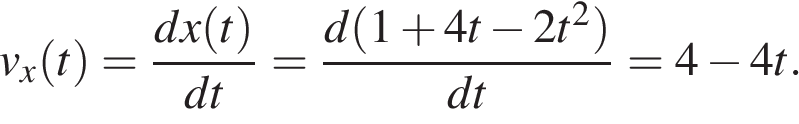
Следовательно, в момент времени  проекция скорости равна
проекция скорости равна

2 способ:
При равноускоренном движении зависимость координаты тела x от времени в общем виде следующая:
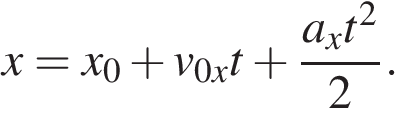
Сравнивая с выражением, данным в условии, получаем, что проекция на ось Ox начальной скорости равна 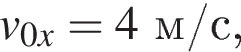 а проекция ускорения равна
а проекция ускорения равна  Таким образом, проекция скорости тела на ось Ox в момент времени
Таким образом, проекция скорости тела на ось Ox в момент времени  равна
равна
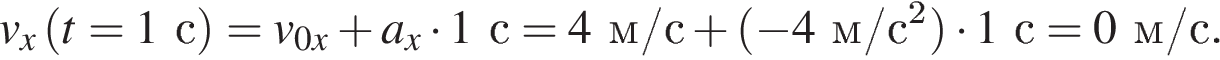
Ответ: 0
6. Зависимость координаты x тела от времени t имеет вид:
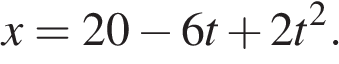
Через сколько секунд после начала отсчета времени t = 0с проекция вектора скорости тела на ось Ox станет равной нулю?
Задание 1 № 115
Решение.
1 способ:
Проекция вектора скорости тела — это производная от соответствующей координаты по времени:
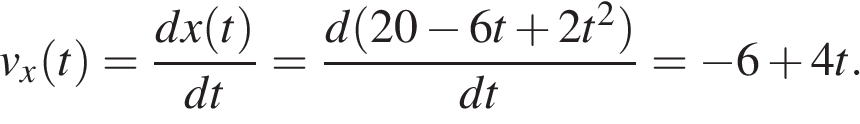
Таким образом, для ответа на вопрос, в какой момент времени проекция скорости обратится в ноль, достаточно решить уравнение: 
2 способ:
При равноускоренном движении зависимость координаты тела x от времени в общем виде имеет вид
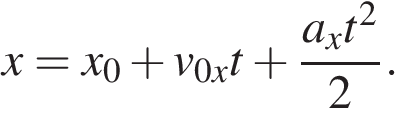
Сравнивая с выражением, данным в условии, получаем, что проекция на ось Ox начальной скорости равна  а проекция ускорения равна
а проекция ускорения равна  Проекция скорости тела на ось Ox зависит от времени следующим образом:
Проекция скорости тела на ось Ox зависит от времени следующим образом:

Следовательно, проекция скорости тела на ось Ox станет равной нулю в момент времени
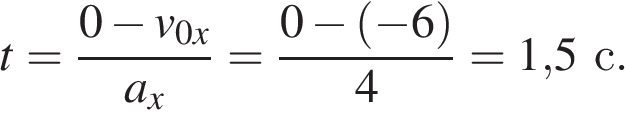
Ответ: 1,5
1,5
7. На рисунке приведен график зависимости проекции скорости тела от времени. Чему равна проекция ускорения тела в момент времени 16 с? Ответ выразите в м/с2.
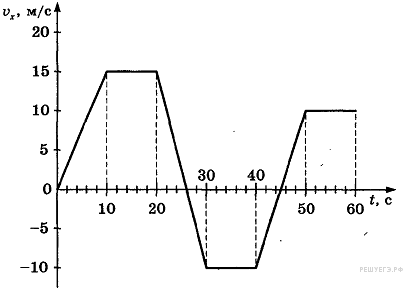
Задание 1 № 116
Решение.
Из графика видно, что в интервале времени от 10 до 20 с проекция скорости тела не изменялась, а значит, проекция ускорения была равна нулю.
Ответ: 0 м/с2
Ответ: 0
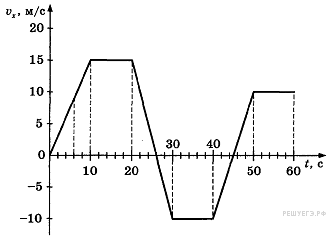
8. На рисунке приведен график зависимости проекции скорости тела от времени. Чему равна проекция ускорения тела в момент времени 6 с? Ответ выразите в м/с2.
Задание 1 № 117
Решение.
Из графика видно, что скорость в интервале времени от 0 с до 10 с меняется линейно, значит, ускорение постоянно. На всём этом интервале времени ускорение такое же, как и в момент времени 6 с. Найдём это ускорение:
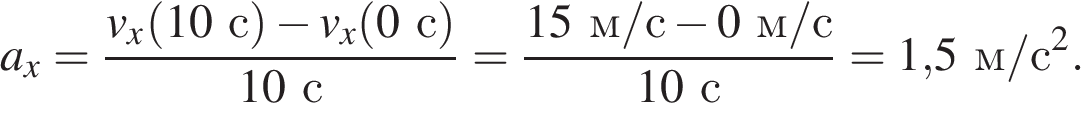
Ответ: 1,5 м/с2
Ответ: 1,5
1,5
9. На рисунке приведен график зависимости проекции скорости тела от времени. Чему равна проекция ускорения тела в момент времени 26 с? Ответ выразите в м/с2.

Задание 1 № 118
Решение.
Из графика видно, что скорость в интервале времени от 20 с до 30 с меняется линейно, значит, ускорение постоянно. На всём этом интервале времени ускорение такое же, как и в момент времени 26 с. Найдём это ускорение:

Ответ: 
Ответ: -2,5
-2,5
10. На рисунке приведен график зависимости проекции скорости тела от времени. Чему равна проекция ускорения тела в момент времени 54 с? Ответ выразите в м/с2.

Задание 1 № 119
Решение.
Из графика видно, что в интервале времени от 50 до 60 с проекция скорости тела не изменялась, а значит, проекция ускорения была равна нулю.
Ответ: 0 м/с2
Ответ: 0
11. На рисунке приведен график зависимости проекции скорости тела от времени. Чему равна проекция ускорения тела в момент времени 45 с? Ответ выразите в м/с2.

Задание 1 № 120
Решение.
Из графика видно, что скорость в интервале времени от 40 с до 50 с меняется линейно, значит, ускорение постоянно. На всём этом интервале времени ускорение такое же, как и в момент времени 45 с. Найдём это ускорение:

Ответ: 2 м/с2
Ответ: 2
12. Тело брошено вертикально вверх. Через 0,5 с после броска его скорость 20 м/с. Какова начальная скорость тела? Сопротивлением воздуха пренебречь. (Ответ дайте в метрах в секунду.)
Задание 1 № 123
Решение.
Поскольку сопротивлением воздуха можно пренебречь, на брошенное тело действует только сила тяжести, которая сообщает ему постоянное ускорение свободного падения, направленное вниз. Следовательно, скорость меняется со временем по закону  Отсюда находим начальную скорость тела
Отсюда находим начальную скорость тела
 .
.
Ответ: 25
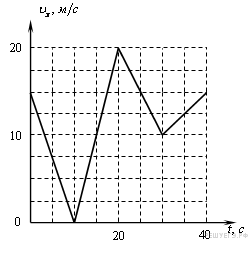
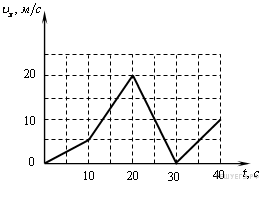
13. Автомобиль движется прямолинейно. На графике представлена зависимость скорости автомобиля от времени. Чему равен минимальный модуль ускорения? Ответ выразите в м/с2.
Задание 1 № 132
Решение.
На всех рассматриваемых интервалах времени скорость автомобиля меняется равномерно, следовательно ускорение на каждом интервале постоянно. Рассчитаем ускорения:
в интервале от 0 до 10 с: 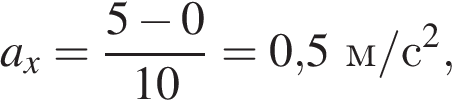
в интервале от 10 до 20 с: 
в интервале от 20 до 30 с: 
в интервале от 30 до 40 с: 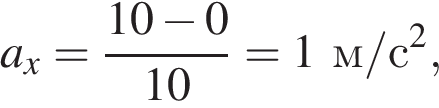
Минимальный модуль ускорения равен 0,5 м/с2.
Ответ: 0,5 м/с2
Ответ: 0,5
0,5
14. Тело брошено вертикально вверх с начальной скоростью 20 м/с. Чему равен модуль скорости тела через 0,5 c после начала отсчета времени? Сопротивление воздуха не учитывать. (Ответ дайте в метрах в секунду.)
Задание 1 № 135
Решение.
Поскольку сопротивлением воздуха можно пренебречь, на брошенное тело действует только сила тяжести, которая сообщает ему постоянное ускорение свободного падения, направленное вниз. Следовательно, скорость меняется со временем по закону  Таким образом, через 0,5 c скорость тела будет равна
Таким образом, через 0,5 c скорость тела будет равна
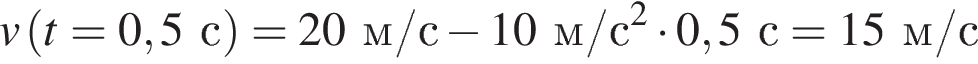 .
.
Ответ: 15
15. Велосипедист съезжает с горки, двигаясь прямолинейно и равноускоренно. За время спуска скорость велосипедиста увеличилась на 10 м/с. Ускорение велосипедиста — 0,5 м/с2. Сколько секунд длился спуск?
Задание 1 № 139
Решение.
Изменение скорости тела связано с ускорением тела и интервалом времени, в течение которого это изменение произошло, соотношением  Следовательно, спуск длился
Следовательно, спуск длился
 .
.
Ответ: 20
16. 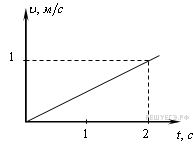 Тело начинает двигаться из начала координат вдоль оси Ox, причем проекция скорости vx меняется с течением времени по закону, приведенному на графике.
Тело начинает двигаться из начала координат вдоль оси Ox, причем проекция скорости vx меняется с течением времени по закону, приведенному на графике.
Чему будет равна проекция ускорения тела ax через 2 c? (Ответ дайте в метрах в секунду в квадрате.)
Задание 1 № 140
Решение.
Из графика видно, что проекция скорости тела возрастала со временем по линейному закону, это означает, что тело двигалось с постоянным ускорением вдоль оси Ox. Таким образом, проекция ускорения тела через 2 c равна
 .
.
Ответ: 0,5
0,5
17.  На графике приведена зависимость скорости прямолинейно движущегося тела от времени. Определите модуль ускорения тела. (Ответ дайте в метрах в секунду в квадрате.)
На графике приведена зависимость скорости прямолинейно движущегося тела от времени. Определите модуль ускорения тела. (Ответ дайте в метрах в секунду в квадрате.)
Задание 1 № 3323
Решение.
Из графика видно, что скорость тела зависит линейно от времени, а значит, его ускорение постоянно. Для определения модуля ускорения можно взять любые две точки на графике: 
Ответ: 10
18. Небольшое тело движется вдоль оси Ox. Его координата x изменяется с течением времени t по закону 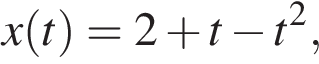
где 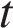 выражено в секундах, а
выражено в секундах, а  — в метрах. Чему равна проекция ускорения этого тела на ось Ox в момент времени
— в метрах. Чему равна проекция ускорения этого тела на ось Ox в момент времени  ? (Ответ дайте в метрах в секунду в квадрате.)Задание 1 № 3699
? (Ответ дайте в метрах в секунду в квадрате.)Задание 1 № 3699
Решение.
1 способ:
Общий вид закона изменения со временем координаты тела при движении с постоянным ускорением имеет вид
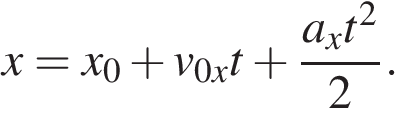
Приведенная в условии зависимость координаты тела от времени 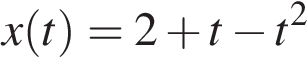 описывается этой квадратичной зависимостью. Приравнивая коэффициенты при t находим, что величина постоянного ускорения
описывается этой квадратичной зависимостью. Приравнивая коэффициенты при t находим, что величина постоянного ускорения 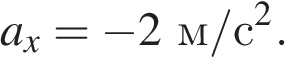
2 способ:
Проекция ускорения тела — это вторая производная координаты тела по времени. Найдём первую производную, тем самым определим зависимость проекции скорости от времени:
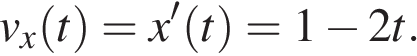
Найдем вторую производную:
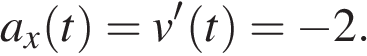
Таким образом, проекция ускорения тела постоянна и равна 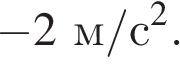
Ответ: 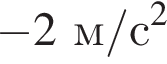
Ответ: -2
-2
Источник: Яндекс: Тренировочная работа ЕГЭ по физике. Вариант 1.
19. Точечное тело начинает движение из состояния покоя и движется равноускоренно вдоль оси Оx по гладкой горизонтальной поверхности. Используя таблицу, определите значение проекции на ось Оx ускорения этого тела. (Ответ дайте в метрах в секунду в квадрате.)
| Момент времени t, c | Координата тела x, м |
| 6,5 | |
Задание 1 № 4338
Решение.
При равноускоренном движении с нулевой начальной скоростью, зависимость координаты тела от времени дается выражением:  где
где  — начальная координата. Из первой строки таблицы ясно, что начальная координата равна 2 м. Используя любую другую строку, например третью, для величины проекции ускорения имеем:
— начальная координата. Из первой строки таблицы ясно, что начальная координата равна 2 м. Используя любую другую строку, например третью, для величины проекции ускорения имеем:
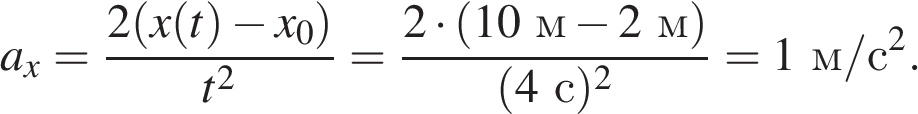
Ответ: 1
Источник: МИОО: Тренировочная работа по физике 11.04.2013 вариант ФИ1501.
20.  На графике приведена зависимость скорости тела от времени при прямолинейном движении. Определите по графику ускорение тела. (Ответ дайте в метрах в секунду в квадрате.)
На графике приведена зависимость скорости тела от времени при прямолинейном движении. Определите по графику ускорение тела. (Ответ дайте в метрах в секунду в квадрате.)
Задание 1 № 4479
Решение.
Из графика видно, что скорость тела линейно зависит от времени, а значит, его ускорение является постоянным, поэтому для поиска ускорения можно использовать любой удобный интервал времени:
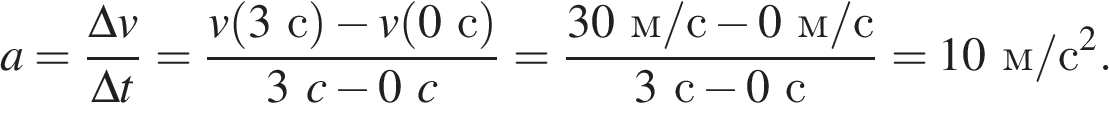
Ответ: 10
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Дальний Восток. Вариант 1.
21. 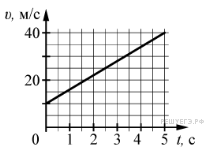 На графике приведена зависимость скорости тела от времени при прямолинейном движении. Определите по графику ускорение тела. (Ответ дайте в метрах в секунду в квадрате.)
На графике приведена зависимость скорости тела от времени при прямолинейном движении. Определите по графику ускорение тела. (Ответ дайте в метрах в секунду в квадрате.)
Задание 1 № 4514
Решение.
Из графика видно, что скорость тела линейно зависит от времени, а значит, его ускорение является постоянным, поэтому для поиска ускорения можно использовать любой удобный интервал времени:

Ответ: 6
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Дальний Восток. Вариант 2.
22.  На графике приведена зависимость проекции скорости vx тела от времени. Определите ускорение тела ax. (Ответ дайте в метрах в секунду в квадрате.)
На графике приведена зависимость проекции скорости vx тела от времени. Определите ускорение тела ax. (Ответ дайте в метрах в секунду в квадрате.)
Задание 1 № 4549
Решение.
Из графика видно, что скорость тела линейно зависит от времени, а значит, его ускорение является постоянным, поэтому для поиска проекции ускорения можно использовать любой удобный интервал времени:

Ответ: 8
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Дальний Восток. Вариант 3.
23. 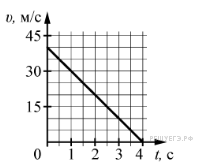 На графике приведена зависимость проекции скорости тела от времени. Определите по графику модуль ускорения тела. (Ответ дайте в метрах в секунду в квадрате.)
На графике приведена зависимость проекции скорости тела от времени. Определите по графику модуль ускорения тела. (Ответ дайте в метрах в секунду в квадрате.)
Задание 1 № 4654
Решение.
Из графика видно, что скорость тела линейно зависит от времени, а значит, его ускорение является постоянным, поэтому для поиска модуля ускорения можно использовать любой удобный интервал времени:
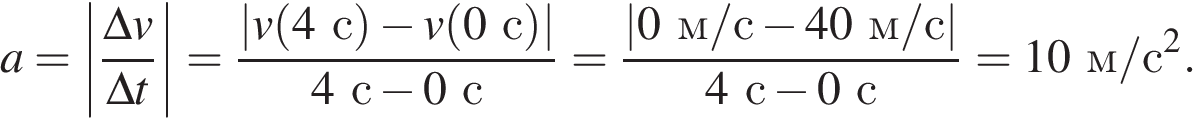
Ответ: 10
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Дальний Восток. Вариант 6.
24. Мальчик съезжает на санках равноускоренно со снежной горки. Скорость санок в конце спуска 10 м/с. Ускорение равно 1 м/с2, начальная скорость равна нулю. Какова длина горки? (Ответ дайте в метрах.)
Задание 1 № 4724
Решение.
Для решения данной задачи удобно использовать так называемую формулу "без времени" для пути, пройденного равноускоренно движущимся телом:
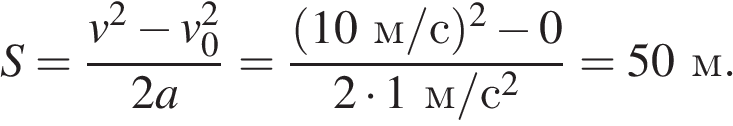
Ответ: 50
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Сибирь. Вариант 1.
25. Автомобиль трогается с места и движется с постоянным ускорением 5 м/с2. Какой путь прошёл автомобиль, если его скорость в конце пути оказалась равной 15 м/с? (Ответ дайте в метрах.)
Задание 1 № 4759
Решение.
Для решения данной задачи удобно использовать так называемую формулу «без времени» для пути, пройденного равноускоренно движущимся телом:
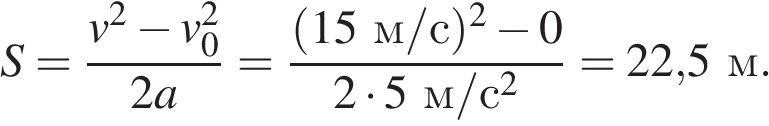
Ответ: 22,5
22,5
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Сибирь. Вариант 2.
26. При равноускоренном движении автомобиля на пути 25 м его скорость увеличилась от 5 до 10 м/с. Чему равно ускорение автомобиля? (Ответ дайте в метрах в секунду в квадрате.)
Задание 1 № 4794
Решение.
Для решения данной задачи удобно использовать так называемую формулу «без времени» для пути, пройденного равноускоренно движущимся телом:
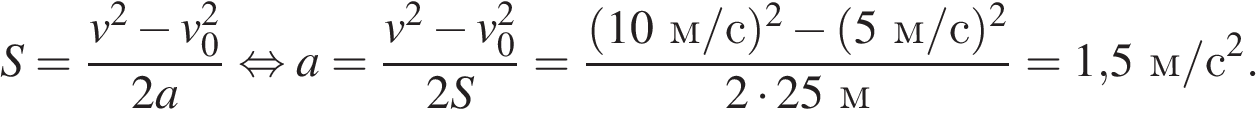
Ответ: 1,5
1,5
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Сибирь. Вариант 3.
27. Велосипедист съезжает с горки, двигаясь равноускоренно. Начальная скорость велосипедиста равна нулю. У основания горки длиной 100 м скорость велосипедиста 10 м/с. Чему равно его ускорение? (Ответ дайте в метрах в секунду в квадрате.)
Задание 1 № 4899
Решение.
Для решения данной задачи удобно использовать так называемую формулу "без времени" для пути, пройденного равноускоренно движущимся телом:
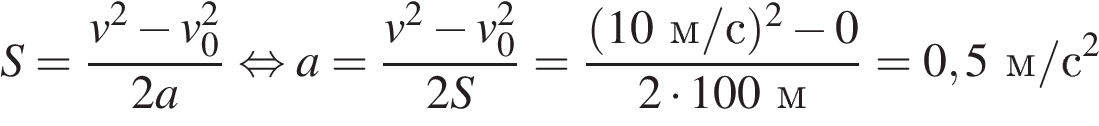
Ответ: 0,5
0,5
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Сибирь. Вариант 6.
28. На рисунке приведён график зависимости проекции скорости тела vx от времени. Чему равна проекции ускорения этого тела ax в интервале времени от 6 с до 10 с? Ответ выразите в м/с2.
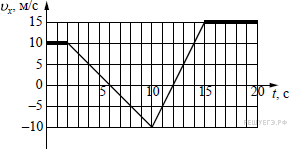
Задание 1 № 6480
Решение.
Ускорение — производная от скорости, или, иначе, тангенс угла наклона графика зависимости скорости от времени. Найдём тангенс угла наклона прямой на интервале от 6 с до 10 с:
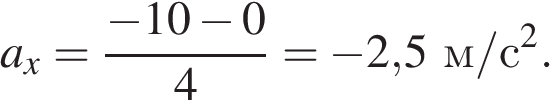
Ответ: 
Ответ: -2,5
-2,5
Источник: Демонстрационная версия ЕГЭ—2015 по физике.
29. На рисунке приведен график зависимости проекции скорости тела от времени. Чему равна проекции ускорения этого тела ax в интервале времени от 5 с до 10 с? Ответ выразите в м/с2.
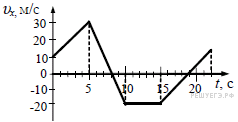
Задание 1 № 6753
Решение.
Ускорение — это производная от скорости по времени или тангенс угла наклона зависимости скорости от времени. В интервале времени от 5 с до 10 с ускорение равно 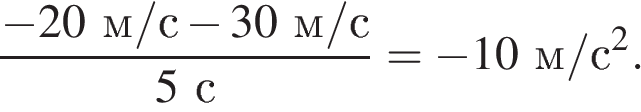
Ответ: 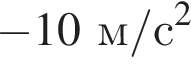
Ответ: -10
-10
Источник: СтатГрад: Диагностическая работа по физике 06.02.2015 Вариант ФИ10402.
30. На рисунке приведён график зависимости проекции скорости тела 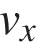 от времени. Чему равна проекции ускорения этого тела
от времени. Чему равна проекции ускорения этого тела 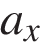 в интервале времени от 0 до 10 с? Ответ выразите в м/с2.
в интервале времени от 0 до 10 с? Ответ выразите в м/с2.
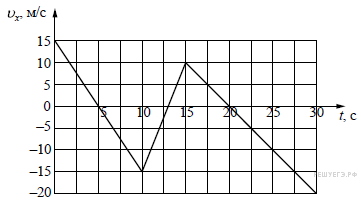
Задание 1 № 6882
Решение.
Из графика видно, что на рассматриваемом интервале скорость меняется равномерно, следовательно ускорение на этом интервале постоянно. Найдем это ускорение:

Ответ: 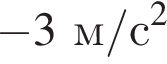
Ответ: -3
-3
Источник: ЕГЭ — 2015. Досрочная волна.
31. Автомобиль движется по прямой улице. На графике представлена зависимость проекции его скорости от времени. Чему равна проекции ускорения автомобиля ax в интервале времени от 10 до 20 с? Ответ выразите в м/с2.
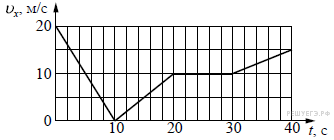
Задание 1 № 7132
Решение.
Из графика видно, что на рассматриваемом интервале скорость меняется равномерно, следовательно ускорение на этом интервале постоянно. Найдем это ускорение:
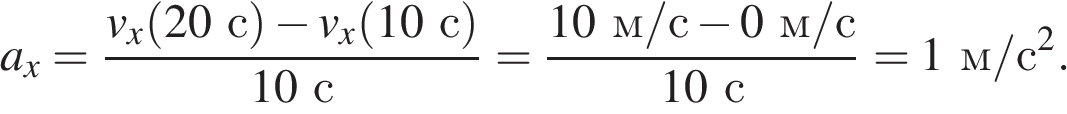
Ответ: 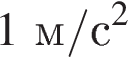
Ответ: 1
Источник: СтатГрад: Репетиционная работа по физике 17.05.2015 Вариант ФИ10802
32. Небольшое тело движется вдоль горизонтальной оси Ox. В момент времени  координата этого тела равна
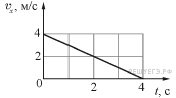
координата этого тела равна 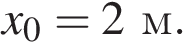 На рисунке приведена зависимость проекции скорости
На рисунке приведена зависимость проекции скорости 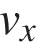 этого тела на ось Ox от времени
этого тела на ось Ox от времени  Чему равна координата тела в момент времени
Чему равна координата тела в момент времени  ?
?
Задание 1 № 8387
Решение.
Из графика видно, что скорость изменяется линейно, то есть движение равноускоренное. Найдём из графика начальную скорость тела, она равна 4 м/с, и ускорение, оно равно –1 м/с2. Координата тела при равноускоренном движении определяется формулой:  Подставив значения начальной координаты, начальной скорости и ускорения в данную формулу, получим:
Подставив значения начальной координаты, начальной скорости и ускорения в данную формулу, получим:

В момент времени  координата тела равна
координата тела равна

Ответ: 10 м
Ответ: 10
33. Небольшое тело движется вдоль горизонтальной оси Ox. В момент времени  координата этого тела равна
координата этого тела равна 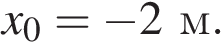 На рисунке приведена зависимость проекции скорости
На рисунке приведена зависимость проекции скорости 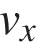 этого тела на ось Ox от времени
этого тела на ось Ox от времени  Чему равна координата тела в момент времени
Чему равна координата тела в момент времени  ?
?

Задание 1 № 8388
Решение.
Из графика видно, что скорость изменяется линейно, то есть движение равноускоренное. Найдём из графика начальную скорость тела, она равна 4 м/с, и ускорение, оно равно –2 м/с2. Координата тела при равноускоренном движении определяется формулой:  Подставив значения начальной координаты, начальной скорости и ускорения в данную формулу, получим:
Подставив значения начальной координаты, начальной скорости и ускорения в данную формулу, получим:
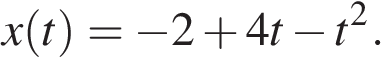
В момент времени  координата тела равна
координата тела равна

Ответ: 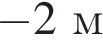
Ответ: -2