Расчётно-графическая работа
по дисциплине
«Теория систем и системный анализ»
ПРИМЕР ИЕРАРХИЧЕСКОЙ КОМПОЗИЦИИ ПРИОРИТЕТОВ
Задача о выборе школы
Выполнила: студентка 1 курса ЭФ группы ПИб-11 Смирнова С.Ю.
Проверила: канд. физ.-мат. наук, доцент Пайзерова Ф.А.
Йошкар-Ола
Оглавление
Введение. 3
ПРИМЕР ИЕРАРХИЧЕСКОЙ КОМПОЗИЦИИ ПРИОРИТЕТОВ.. 5
Критерии выбора школы.. 6
Метод анализа иерархии Саати. 7
Заключение. 20
Список литературы.. 23
1.
Введение
В данной расчетно-графической работе будем рассматривать метод анализа иерархий. Цель метода анализа иерархий - разработка теории и методологии для моделирования неструктурированных задач в экономике, науке управления и социальных наука.
Метод анализа иерархий представляется более обоснованным путем решения многокритериальных задач в сложной обстановке с иерархическими структурами, включающими как осязаемые, так и неосязаемые факторы, чем подход, основанный на линейной логике. Применяя дедуктивную логику, исследователи проходят трудный путь построения тщательно осмысленных логических цепей только для того, чтобы в итоге, полагаясь на одну лишь интуицию, объединить различные умозаключения, полученные из этих дедуктивных посылок. Кроме того, подход, основанный на логических цепях, может не привести к наилучшему решению, так как в данном случае может быть потеряна возможность принятия компромиссов между факторами, лежащими в разных цепях логического мышления.
Метод анализа иерархий является замкнутой логической конструкцией, обеспечивающей с помощью простых правил анализ сложных проблем во всем их разнообразии и приводящей к наилучшему ответу. К тому же, применение метода позволяет включить в иерархию все имеющееся у исследователя по рассматриваемой проблеме знание и воображение. Это, с моей точки зрения, является балансированным путем решения трудной проблемы: оставить математику простой и позволить богатству структуры нести бремя сложности. Никакая математика не может заменить человеческий ум и опыт интерпретации реального мира. Независимо от того, насколько сложной может быть математика, она всё же не будет отражать все те элементы в проблеме, которые явно существенны для нас.
|
|
Сам метод заключается в декомпозиции проблемы на более простые составляющие части и поэтапном установлении приоритетов оцениваемых компонентов с использованием попарных сравнений. На первом этапе выделяются наиболее важные элементы проблемы, на втором – наилучший способ проверки наблюдений испытания и оценки элементов, на третьем – осуществляется выработка способа применения решения и оценка его качества. Весь процесс подвергается проверке и осмыслению до тех пор, пока не будет уверенности, что процесс охватил все важные характеристики, необходимые для предоставления проблемы и ее решения.
ПРИМЕР ИЕРАРХИЧЕСКОЙ КОМПОЗИЦИИ ПРИОРИТЕТОВ
Задача о выборе школы
Был проведен анализ трех школ A, B и C на предмет их желательности с точки зрения ученика 10 класса. Для сравнения были выбраны семь независимых характеристик: учеба, друзья, школьная жизнь, профессиональное обучение, подготовка к ВУЗУ, школьные кружки и питание
На первом уровне – цель – школа.
|
|
На втором уровне – 7 критериев, уточняющих цель.
На третьем уровне – 3 альтернативы (разные школы).
| ШКОЛА |
| Школа В |
| Школа Б |
| Школа А |







Критерии выбора школы:
1) Учеба (выбор класса с уклоном по желанию: гуманитарный, социально-экономический, универсальный, биолого-химический, информационный и т.д.)
2) Друзья (хорошие отношения с одноклассниками, с друзьями по школе и т.п.)
3) Школьная жизнь (активное участие в жизни класса и школы, активная общественная деятельность, участие в школьном научном обществе)
4) Дополнительное обучение (художественная школа, школа начинающих фотографов, школа начинающих программистов, вождение, курсы повара и многое другое)
5) Подготовка к ВУЗу (элективные курсы, факультативы, центр довузовской подготовки)
6) Школьные кружки (швейный кружок, круг любителей животных, кружок экологов и т.д.)
7) Питание (хорошее питание, столовая, буфет).
После иерархического изображения проблемы возникает вопрос: как установить приоритеты критериев и оценить каждую из альтернатив по критериям, выявив самую важную из них. Когда проблема представлена иерархически составляется матрица для сравнения относительной важности критериев на втором уровне к общей цене на первом. Составим матрицу попарных сравнений для 2 уровня.
Метод анализа иерархии Саати
Целью построений является получение приоритетов элементов на последнем уровне, наилучшим образом отражающих относительное воздействие на вершину иерархии.
После иерархического или сетевого воспроизведения проблемы возникает вопрос: как установить приоритеты критериев и оценить каждую из альтернатив по критериям, выявив самую важную из них?
|
|
В МАИ элементы задачи сравниваются попарно по отношению к их взаимодействию на общую для них характеристику. Когда проблемы представлены иерархически, составляется матрица для сравнения относительной важности критериев на втором уровне по отношению к общей цели на первом уровне. Подобные матрицы должны быть построены для парных сравнений каждой альтернативы на третьем уровне по отношению к критериям второго уровня.
Для проведения субъективных парных суждений разработана шкала. Эта шкала оказалась эффективной не только во многих приложениях, ей правомочность доказана теоретически при сравнении со многими другими шкалами.
Шкала относительной важности
| Интенсивность относительной важности | Определение | Объяснение |
| Равная важность | Равный вклад двух видов деятельности в цель | |
| Умеренное превосходство одного над другим | Опыт и суждения дают легкое превосходство одному виду деятельности над другим | |
| Существенное или сильное превосходство | Опыт и суждения дают сильное превосходство одному виду деятельности вал другим | |
| Значительно превосходство | Одному виду деятельности дается настолько сильное превосходство, что оно становится практически значительным | |
| Очень сильное превосходство | Очевидность превосходства одного вида деятельности над другим подтверждается наиболее сильно | |
| 2, 4, 6, 8 | Промежуточные решения между двумя соседними суждениями | Применяются в компромиссном случае |
| Обратные величины, приведенных выше чисел | Если при сравнении одного вида деятельности с другим получено одно из вышеуказанных чисел (например 3). то при сравнении второго вида деятельности с первым получим обратную величину (т е. 1/3) |
Для заполнения матриц по критериям для школ А, Б, В дадим их характеристики:
| ШКОЛА | Учёба | Друзья | Школьная жизнь | Дополни тельное обучение | Подго-товка к ВУЗу | Школьные кружки | Пита-ние |
| Учеба | |||||||
| Друзья | 1/3 | ||||||
| Школьная жизнь | 1/5 | 1/3 | |||||
| Дополни тельное обучение | 1/8 | 1/2 | 1/3 | 1/3 | |||
| Подготовка к ВУЗу | 1/6 | 1/2 | 1/2 | 1/3 | |||
| Школьные кружки | 1/7 | 1/4 | 1/3 | 1/3 | 1/5 | ||
| Питание | 1/6 | 1/3 | 1/4 | 1/3 | 1/4 |
Теперь перейдем к парным сравнениям элементов на нижнем уровне. Сравниваемые попарно элементы — это возможные варианты выбора места отдыха. Получаем семь матриц суждений размерностью 3X3, поскольку имеется семь критериев на втором уровне и три дома, которые попарно сравниваются по каждому из критериев. Матрицы вновь содержат суждения студентки. Для того чтобы понять суждения, дадим краткое описание мест отдыха.
Для выявления меры удовлетворения кандидата школой сначала следует перечислить важнейшие критерии, характеризующие школы, и вычислить сравнительную желательность этих критериев для кандидата. Желательность будет меняться от одного кандидата к другому.
Школа А – эта школа для получения качественного образования и хорошей подготовки для поступления в высшее учебное заведение. В школе существует 5 классов с различным уклоном. Меню в столовой предполагает двухразовое питание учащихся. В школе множество различных кружков и секций, что создает в школе дружескую атмосферу и возможность проявить свои таланты в творчестве и спорте.
Школа Б – эта школа активно участвует во всех общественных делах, проводит мероприятия в рамках города. Есть столовая. В этой школе 2 класса с уклонами. Есть кружок экологов. Средняя подготовка к ВУЗу. Нет возможности получить дополнительное образование.
Школа В – эта обычная школа, где можно получить среднее образования, по окончании которого выдается аттестат. Школа участвуют во всех проводимых мероприятиях. Есть столовая. Созданы условия, чтобы классы были дружными. В данной школе нет профильного разделения и все классы универсальные.
Далее построим 7 матриц для каждой школы:
| Учёба | А | Б | В |
| А | |||
| Б | 1/3 | ||
| В | 1/5 | 1/3 |
| Друзья | А | Б | В |
| А | |||
| Б | 1/6 | ||
| В | 1/6 | 1/2 |
| Школьная жизнь | А | Б | В |
| А | 1/3 | ||
| Б | |||
| В | 1/4 | 1/4 |
| Питание | А | Б | В |
| А | |||
| Б | 1/5 | ||
| В | 1/7 | 1/2 |
| Профессиональное обучение | А | Б | В |
| А | |||
| Б | 1/7 | 1/3 | |
| В | 1/6 |
| Подготовка к ВУЗу | А | Б | В |
| А | |||
| Б | 1/3 | ||
| В | 1/6 | 1/3 |
| Школьные кружки | А | Б | В |
| А | |||
| Б | 1/5 | 1/3 | |
| В | 1/4 |
Индекс согласованности для каждой матрицы и для всей иерархии можно приближенно вычислить следующим образом:
1) Сначала суммируется каждый столбец суждений.
2) Сумма первого столбца умножается на величину первой компоненты нормализованного вектора приоритетов.
3) Полученные числа суммируются.
Таким образом, получим величину λmax. Для индекса согласованности имеем формулу ИС =  , где n - число сравниваемых элементов.
, где n - число сравниваемых элементов.
Запишем таблицу средних значений согласованности для случайных матриц разного порядка:
| Размер матрицы | ||||||||||
| Случайная согласованность | 0,58 | 0,9 | 1,12 | 1,24 | 1,32 | 1,41 | 1,45 | 1,49 |
ОС = 
Из группы матриц парных сравнений формируем набор локальных приоритетов, которые выражают относительные влияние множества элементов. Каждая из этих матриц обладает свойством обратной симметричности. Для каждой матрицы необходимо вычислить собственные вектора. Затем нормализовать их к единице, тем самым будет получен вектор приоритетов.
Находим среднее геометрическое, вектор, индекс согласованности, ОС и λ для каждой матрицы:
1) Для первой матрицы УЧЁБА мы нашли:
| Учёба | А | Б | В | Вектор | Ср.геом. | λ | ИС: | ОС: |
| А | 0,6370 | 2,4662 | 3,0385 | 0,0193 | 0,0332 | |||
| Б | 1/3 | 0,2583 | 1,0000 | |||||
| В | 1/5 | 1/3 | 0,1047 | 0,4055 | ||||
| Cумма S: | 1,5333 | 4,3333 | 9,0000 | 1,0000 | 3,8717 |
Среднее геометрическое находится по формуле:
А: a=  =
=  =2,4662
=2,4662
Б:  =
=  =1
=1
В: c =  =
=  =0,4055
=0,4055
S(cр.геом.)= a+b+c =2,4662+1+0,4055= 3,8717
Вектор находится по формуле:
х 1 =a/S=2,4662/3,8717=0,6370
x2=b/S=1/3,8717=0,2583
x3=c/S=0,4055/3,8717=0,1047
В сумме векторов должна получиться 1.
Проверим:
х1+ х2+ х3=0,6370+0,2583+0,1047=1
Чтобы найти λ, нужно сумму столбца А умножить на соответствующий вектор А, сумму столбца Б умножить на соответствующий вектор Б и сумму столбца В умножить на с вектор В:
λ= 1,5333* 0,6370+ 4,3333* 0,2583+0,1047*9=3,0385
ИС =  =
=  =
=  =0,0193
=0,0193
n =3- число сравниваемых элементов
ОС =  =
=  =0,0332=3%
=0,0332=3%
Чтобы найти случайную согласованность, нужно воспользоваться таблицей. Случайная согласованность, для n=3 равна 0,58.
Остальные матрицы вычисляются аналогично первой матрице.
2) Находим среднее геометрическое, вектор, индекс согласованности, ОС и λ для матрицы для второй матрицы ДРУЗЬЯ:
| Друзья | А | Б | В | Вектор | Ср.геом. | λ | ИС: | ОС: |
| А | 0,7450 | 3,3019 | 3,0536 | 0,0268 | 0,0462 | |||
| Б | 1/6 | 0,1564 | 0,6934 | |||||
| В | 1/6 | 1/2 | 0,0986 | 0,4368 | ||||
| Cумма S: | 1,3333 | 7,5000 | 9,0000 | 1,0000 | 4,4321 |
λ= 3,0536
ИС=0,0268
ОС=0,0462=5%
3) Находим среднее геометрическое, вектор, индекс согласованности, ОС и λ для матрицы ШКОЛЬНАЯ ЖИЗНЬ:
| Школьная жизнь | А | Б | В | Вектор | Ср.геом. | λ | ИС: | ОС: |
| А | 1/3 | 0,2906 | 1,1006 | 3,1356 | 0,0678 | 0,1169 | ||
| Б | 0,6046 | 2,2894 | ||||||
| В | 1/4 | 1/4 | 0,1048 | 0,3969 | ||||
| Cумма S: | 4,2500 | 1,5833 | 9,0000 | 1,0000 | 3,7869 |
λ= 3,1356
ИС=0,0678
ОС=0,1169=12%
4) Находим среднее геометрическое, вектор, индекс согласованности, ОС и λ для матрицы ПРОФЕССИОНАЛЬНОЕ ОБУЧЕНИЕ:
| Дополни- тельное обучение | А | Б | В | Вектор | Ср.геом. | λ | ИС: | ОС: |
| А | 0,7504 | 3,4760 | 3,0999 | 0,0500 | 0,0861 | |||
| Б | 1/7 | 1/3 | 0,0782 | 0,3625 | ||||
| В | 1/6 | 0,1713 | 0,7937 | |||||
| Cумма S: | 1,3095 | 11,0000 | 7,3333 | 1,0000 | 4,6322 |
λ= 3,0999
ИС=0,0500
ОС=0,0861=9%
5) Находим среднее геометрическое, вектор, индекс согласованности, ОС и λ для матрицы ПОДГОТОВКА К ВУЗу:
| Подготовка к ВУЗу | А | Б | В | Вектор | Ср.геом. | λ | ИС: | ОС: |
| А | 0,0953 | 0,3816 | 3,0183 | 0,0091 | 0,0158 | |||
| Б | 1/3 | 0,2499 | 1,0000 | |||||
| В | 1/6 | 1/3 | 0,6548 | 2,6207 | ||||
| Cумма S: | 10,000 | 4,333 | 1,500 | 1,000 | 4,002 |
λ= 3,0183
ИС=0,0091
ОС=0,0158=2%
6) Находим среднее геометрическое, вектор, индекс согласованности, ОС и λ для матрицы ПИТАНИЕ:
| Питание | А | Б | В | Вектор | Ср.геом. | λ | ИС: | ОС: |
| А | 0,7396 | 3,2711 | 3,0142 | 0,0071 | 0,0122 | |||
| Б | 1/5 | 0,1666 | 0,7368 | |||||
| В | 1/7 | 1/2 | 0,0938 | 0,4149 | ||||
| Cумма S: | 1,3429 | 6,5000 | 10,0000 | 1,0000 | 4,4228 |
λ= 3,0142
ИС=0,0071
ОС=0,0122=1%
7) Находим среднее геометрическое, вектор, индекс согласованности, ОС и λ для матрицы ШКОЛЬНЫЕ КРУЖКИ:
| Школьные кружки | А | Б | В | Вектор | Ср.геом. | λ | ИС: | ОС: |
| А | 0,6738 | 2,7144 | 3,0858 | 0,0429 | 0,0739 | |||
| Б | 1/5 | 1/3 | 0,1007 | 0,4055 | ||||
| В | 1/4 | 0,2255 | 0,9086 | |||||
| Cумма S: | 1,4500 | 9,0000 | 5,3333 | 1,0000 | 4,0285 |
λ= 3,0858
ИС=0,0429
ОС=0,0739=7%
И найдем результаты для последней матрицы n=7
| ШКОЛА | Вектор | Ср.геом. | λ | ИС: | ОС: |
| Учеба | 0,4495 | 4,3660 | 7,8108 | 0,1351 | 0,10237 |
| Друзья | 0,1790 | 1,7385 | |||
| Школьная жизнь | 0,1288 | 1,2512 | |||
| Профессиональное обучение | 0,0693 | 0,6730 | |||
| Подготовка к ВУЗу | 0,0823 | 0,7992 | |||
| Школьные кружки | 0,0453 | 0,4396 | |||
| Питание | 0,0458 | 0,4453 | |||
| Сумма: | 1,0000 | 9,71 |
λ= 7,8108
ИС=(7,8108-7)/6=0,1351
ОС=0,1351/1,32=0,1023=10%
Среднее геометрическое находится по формуле в Excel ->функция
f(x)->СРГЕОМ, выделяем каждую строку матрицы и задаем эту функцию, получится результат:
 ;
;
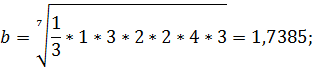





a+b+c+d+e+f+g=9,71
Вектор находится по формуле:







В сумме векторов должна получиться 1.

=7,8108
 0,1351=13%.
0,1351=13%.
n =7- число сравниваемых элементов
 .
.
CC находим по таблице случайной согласованности, где для n=7 СС=1,32.
Явным лидером по критерию учеба является школа А.
По критериюшкольная жизнь превосходит остальные учебные заведения школа Б.
Школа В – обычная школа, во многом уступающая от школ А и Б.
Следующим этапом является применение принципа синтеза. Для определения главных приоритетов в матрице локальные приоритеты располагаются по отношению к каждому критерию. Каждый столбец векторов умножается на приоритет соответствующего критерия, и результат складывается вдоль каждой строки.
| ШКОЛА | Учёба | Друзья | Школь-ная жизнь | Профес-сиональное обучение | Подго- товка к ВУЗу | Школьные кружки | Пита-ние |
| 0,4495 | 0,179 | 0,1288 | 0,0693 | 0,0823 | 0,0453 | 0,0458 | |
| А | 0,637 | 0,745 | 0,2906 | 0,7504 | 0,0953 | 0,6738 | 0,7396 |
| Б | 0,2583 | 0,1564 | 0,6046 | 0,0782 | 0,2499 | 0,1007 | 0,1666 |
| В | 0,1047 | 0,0986 | 0,1048 | 0,1713 | 0,6548 | 0,2255 | 0,0938 |
Для школы А имеем: 0,4495*0,637+0,745*0,179+0,2906*0,1288+ +0,7504*0,0693+0,0953*0,0823+0,6738*0,0453+0,7396*0,0458=0,578
Для школы Б имеем: 0,4495*0,2583+0,1564*0,179+0,6046*0,1288+ +0,0782*0,0693+0,2499*0,0823+0,1007*0,0453+0,1666*0,0458=0,262
Для школы В имеем: 0,4495*0,1047+0,0986*0,179+0,1048*0,1288+ +0,1713*0,0693+0,6548*0,0823+0,2255*0,0453+0,0938*0,0458=0,161
Проанализировав данные 3 школ, пришли к выводу, что наиболее перспективной школой для ученика 10 класса является школа А, т.к. эта школа является образцовым для получения качественного образования и хорошей подготовки для поступления в высшее учебное заведение, чем школы Б и В. Хотя школа
Школа А, которая была наименее желательна с точки зрения школьной жизни, оказалась победителем. Именно туда ученик 10 класса и пойдет учиться.
При анализе можно убедиться, что исход не был удивительным, если принять во внимание тот факт, что Школа А превосходила остальные школы по пяти из семи критериев.
Заключение
Конечно, есть моменты, когда могут действовать политические пристрастия, скрытые «домашние заготовки», раскол и другие мотивы. В этом случае взаимодействие и сотрудничество в группе затрудняются. Мы сталкивались с такими проблемами на практике при использовании метода анализа иерархии (МАИ). Наше заключение таково, что МАИ является мощным средством для тех, кто хочет оценить как свои стратегии, так и стратегии своих оппонентов. Тех, кто не желает участвовать в процессе, нельзя заставить, однако их иногда можно убедить. Процесс движется быстрее, если участники имеют общие цели, долговременный близкий контакт, работу в климате социального одобрения и одинаковый статус.
Последним замечанием является то, что взаимодействие не похоже на брак, о котором люди склонны иметь романтические представления, однако после вступления в него они сталкиваются с множеством трений, ссор и разногласий. Тем не менее, в общем, жизнь продолжается, и имеются фундаментальные точки согласия и общие потребности, которые удерживают людей друг с другом. Поэтому входить в процесс группового взаимодействия никто не должен со слишком большими надеждами и сильным предрасположением к правильности и порядку.
Метод анализа иерархий успешно применялся во многих областях, в частности: при разработке плана распределения энергии в промышленности или проектировании транспортной системы для Судана, в планировании будущего корпорации и измерении факторов окружающей среды на ее развитие; при построении сценариев высшего образования в США; при выдвижении кандидатов и в процессах выборов.
К сильным сторонам МАИ можно отнести то, что при определении иерархии обычно важную роль также играют знания лиц, производящих суждения для парных сравнений.
Оказалось, что использование МАИ стимулировало повышение уровня знаний о специфических проблемах планирования даже среди людей, которые имеют достаточно обширные познания и опыт в данной конкретной ситуации. Более того, проблема еще больше раскрывается, и накапливаются дополнительные знания.
Подход к измерениям с помощью МАИ допускает определенную степень несогласованности. Группа людей может принять решение при допустимой степени несогласованности для каждого из членов группы. В этом случае они не будут чувствовать, что их предпочтения были в значительной степени нарушены.
Метод анализа иерархий основан на следующих аксиомах: парных сравнений, обоснованной шкалы для перевода суждений в числа с помощью парных сравнений и обратносимметричных отношений, гомогенной кластеризации иерархических уровней, иерархической композиции путем взвешивания и сложения и, наконец, на аксиоме ожидании, которая отражает соответствие заложенных в иерархию элементов ожидаемым результатам. Из этих аксиом получено несколько теорем, которые превращают МАИ в математически обоснованный подход для получения шкал отношений при решении сложных проблем.
Список литературы
1. Саати Т., Керис К. Аналитическое планирование. Организация систем: Пер. с англ – М. Радио и связь, 1991 – 224 с: ил. – ISBN 5-256-0038-1
2. Саати Т. Принятие решений. Метод анализа иерархий. М.: Радио и связь, 1993 – 278 c.