Для того, чтобы произвести синтез корректирующего устройства необходимо перейти от непрерывной модели объекта к дискретной,
с использованием интервала дискретности 0.006 секунди экстраполятором нулевого значения:
>>Ts=0.006;
>>Wd=c2d(W,Ts,'zoh')
Transferfunction:
6.287e-005 z + 6.283e-005
-------------------------
z^2 - 1.98 z + 0.9982
Samplingtime: 0.006
Для проверки качества выполненной аппроксимации необходимо сравнить частотные характеристики исходной непрерывной и полученной дискретной модели:
| Рис. 2. Частотные характеристики непрерывной и дискретной моделей |
>> bode(W,'-',Wd,'--')
Далее построим переходной процесс для дискретной системы:
>>step(Wd)
| Рис. 3. Переходной процесс в дискретной системе |
Проанализировав график переходного процесса в дискретной системе, можно сделать вывод, что в системе присутствует ярко выраженная колебательность, причиной которой является слабое демпфирование.
В этом можно убедиться, вычислив полюсы дискретной модели:
>> %Полюсы дискретной модели
>>damp(Wd)
EigenvalueMagnitude Equiv. Damping Equiv. Freq. (rad/s)
9.90e-001 + 1.34e-001i 9.99e-001 6.71e-003 2.24e+001
9.90e-001 - 1.34e-001i 9.99e-001 6.71e-003 2.24e+001
Полюсы расположены в близи единичной окружности и имеют малое демпфирование.
Данный результат позволяет конкретизировать задачу проектирования:необходимо рассчитать регулятор, который увеличит демпфирования данных полюсов. Наиболее простой вариант решения этой задачи подбор коэффициента усиления системы, который можно осуществить
с помощью метода корневого годографа:
>> rlocus(Wd),zgrid
| Рис. 4. Корневой годограф исследуемой системы |
Проанализировав корневой годограф, можно сказать, что с увеличением коэффициента усиления полюсы замкнутой системы быстро выходят за пределы единичной окружности и система становится неустойчивой. Поэтому введем некоторую динамическую коррекцию в виде дискретного компенсатора с передаточной функцией:
|
|
где 
, 
, 
Далее формируется разомкнутая модель контура как последовательное соединение моделей объекта и компенсатора:
>> D=zpk(0.85,0,1,Ts) %Формирование модели компенсатора
Zero/pole/gain:
(z-0.85)
--------
z
Samplingtime: 0.006
>>oloop=Wd*D %Формированиеразомкнутогоконтура
Zero/pole/gain:
6.2868e-005 (z+0.9994) (z-0.85)
-------------------------------
z (z^2 - 1.98z + 0.9982)
Sampling time: 0.006
Далее можно определить, как компенсатор модифицирует ЛЧХ магнитной головки:
>> bode(Wd,'--',oloop,'-')
| Рис. 5. Частотные характеристики магнитной головки и разомкнутого контура |
На Рис. 5 частотная характеристика магнитной головки показана пунктирной линией, а частотная характеристика контурас компенсатором – сплошной линией.
Из анализа характеристик следует, что компенсатор сдвигает фазовую характеристику вверх (вводит опережение) в диапазоне частот от 10 до 980 рад/с.
Теперь необходимо построить корневой годограф для контура
с компенсатором:
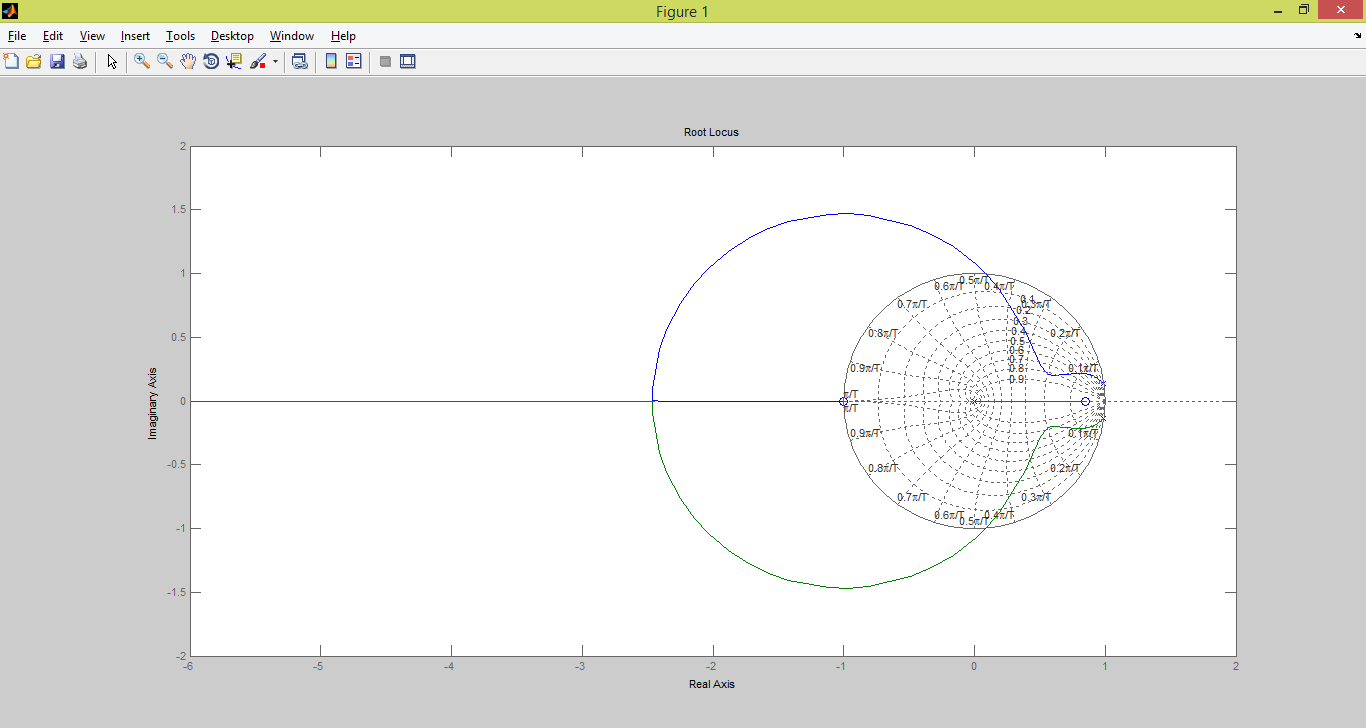
| Рис. 6. Корневой годограф для контура с компенсатором |
Теперь полюсы остаются внутри единичной окружности для большего диапозона значений коэффициента усиления.
Далее необходимо указать оптимальное, на ваш взгляд, расположение полюсов, для этого необходимо воспользоваться функцией rlockfind:
>> [k,poles]=rlocfind(oloop)
Select a point in the graphics window
selected_point =
0.5889 + 0.0039i
k =
4.0395e+003
poles =
0.5687 + 0.2072i
0.5687 - 0.2072i
|
|
0.5888
Определим демпфирование замкунтой системы:
>> ddamp(poles,Ts)
Eigenvalue Magnitude Equiv. Damping Equiv. Freq. (rad/s)
5.69e-001 + 2.07e-001i 6.05e-001 8.21e-001 1.02e+002
5.69e-001 - 2.07e-001i 6.05e-001 8.21e-001 1.02e+002
5.89e-001 5.89e-001 1.00e+000 8.83e+001
Чтобы оценить результаты синтеза, сформируем замкнутую систему и построим для нее переходную функцию:
>> cloop=feedback(oloop,k)
Zero/pole/gain:
6.2868e-005 (z+0.9994) (z-0.85)
----------------------------------
(z-0.5888) (z^2 - 1.137z + 0.3664)
Sampling time: 0.006
| Рис. 7. Переходной процесс в замкнутой системе с компенсатором |
Полученный переходной процесс имеет время установления около
16 периодов дискретизации, то есть 0.09 секунд.
Оценим работоспособность полученной системы. Класическими критериями работоспособности являются запасы устойчиовсти по фазе и амплитуде. Для их орпеделеня воспользуемся функцией margin, предварительно учтя найденное с помощью фукции rlocfindзначение k:
>> olk=k*oloop;
>> [Gm,Pm,Wcg,Wcp]=margin(olk);
>> Margins=[Gm WcgPm Wcp]
Margins =
3.8463 247.3058 43.5555 86.0925
>>margin(olk)
| Рис. 8. ЛАЧХ и ФАЧХ с показанными запасами устойчивости |
Рассмотренная система является работоспособной, поскольку имеет запас устойчивости по амплитуде равный 11.7 Дб и запас устойчивости по фазе равный 43.6°.