| Сила | Положение механизма | |||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
| Q,H |
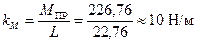/мм
Поскольку цикл машины соответствует одному обороту ведущего звена, то приведенные силы и их моменты отыскиваются для двенадцати положений механизма. В соответствии с результатами расчета на чертежном листе строится диаграмма приведенных моментов в функции угла φ поворота кривошипа.
| Приведенные сила, момент | Положение механизма | |||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
| Fпр, Н | 3648,00 | 5011,20 | 5078,40 | 2931,20 | ||||||||
| Mпр, Н | 1094,40 | 1503,36 | 1523,52 | 879,36 |
2. Путем графического интегрирования диаграммы приведенных моментов строится диаграмма работ заданных сил сопротивления (Ас─ φ) за цикл. На этом же графике строится диаграмма работ движущихся сил. При этом предполагается, что приведенный движущий момент есть величина постоянная. Следовательно, работа этого момента будет выражаться прямолинейной зависимостью в системе координат «А Д – φ».
На полученной диаграмме работ ординаты поля между криволинейным графиком, изображающим работу сил сопротивления, и прямолинейным, отображающим работу движущих сил, будут определять собой разность работ, или приращение кинетической энергии машины.
Замеряя разность ординат D А= А Д - А С для каждого положения механизма, строим диаграмму разности работ – диаграмму приращения кинетической энергии.
3. Приведение моментов инерции
Приведенный момент инерции определяется для каждого положения механизма по формуле
.
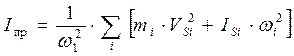Масштаб диаграммы приведенных моментов инерции:
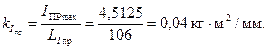
| Приведенный момент инерции | Положение механизма | |||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
| I, кг·м2*10-4 | 2,463 | 2,975 | 3,4239 | 3,36 | 3,24 | 2,7462 | 2,5529 | 2,2,4966 | 2,7654 | 3,6393 | 4,5125 | 3,3883 |
4. Расчет маховика.
Определяем углы 
и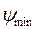 
по выражениям
C использованием данных диаграммы разности работ «Δ A ─ φ» и диаграммы приведенных моментов инерции «I пр – φ» строим диаграмму кинетической энергии в функции приведенного момента инерции «Δ A ─ I пр» ─ диаграмму Виттенбауэра. К полученной замкнутой кривой проводим наклоненные к оси абсцисс две касательные: снизу под углом 
к оси абсцисс и сверху под углом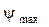 
.Касательные пересекают ось ординат в точках А и В. Приведенный момент инерции маховика
Средний диаметр обода маховика
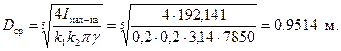
Здесь
а и b – размеры поперечного сечения обода маховика;
γ – плотность материала маховика, кг/м3.
Определив Dср, находим
5. Нахождение величины махового момента инерции маховика по методу Мерцалова
Для контроля последних этапов расчета маховика и окончательного результата производим проверку по методу Мерцалова.
Δ T м = Δ T– Δ T им ,
где Δ T м─ приращение кинетической энергии маховика;
Δ T ─ приращение кинетической энергии машины;
Δ T им─ приращение кинетической энергии исполнительного механизма. (см. табл. 7)
Диаграмма приращения кинетической энергии звеньев механизма строится путем использования приближенного выражения
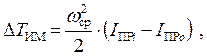
где 
─ приведенный момент инерции звеньев механизма в начальном положении;
─ приведенный момент инерции звеньев механизма в остальных промежуточных положениях механизма. (см. табл. 6)
Таблица 6
Приращение кинетической энергии исполнительного механизма.
| Приращение кин. энергии исп. мех-ма | Положение механизма | |||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
| ∆Тим, м | 0,0 | 27,1035 | 52,81 | 49,16457 | 42,58737 | 14,333 | 4,92741 | 1,8416 | 16,5745 | 64,473 | 112,33 | 50,7156 |
| Приращение кин. энергии маховика | Положение механизма | |||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
| ∆Тм, м | 0,0 | 32,857 | -42,384 | 114,172 | -231,067 | -133,644 | -17,555 | 117,518 | 90,3055 | -116,003 | -315,448 | -231,877 |
Замеряем по оси ординат расстояние между самой верхней и самой нижней точками диаграммы изменения кинетической энергии машины и маховика, находим отрезок CD, затем определяем приведенный момент инерции маховика:
где kT – масштаб диаграммы Δ T.
Определяем погрешность результатов, полученных методами Виттенбауэра и Мерцалова
.