Урок в Zoom
Запишите число, классная работа, тему урока.
Классная работа. 12.11.20
Перпендикуляр к прямой. Медианы, биссектрисы и высоты треугольника.
1. ZOOM
2. если у вас нет возможности выйти в ZOOМ, посмотри видео https://resh.edu.ru/subject/lesson/7291/main/249774/ - РЭШ
Цифровая школа Оренбуржья - https://77.41.182.159/theme.php?id=339
3. Прочитай параграф в учебнике (16,17)
Модуль (теоретический)
Разбери и выучи!
Перпендикуляр от точки к прямой
ü Отрезок AC называется перпендикуляром, проведённым из точки A прямой a, если прямые AC и a перпендикулярны.
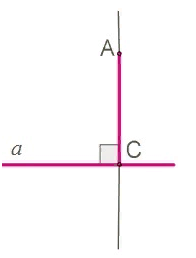Точка C называется основанием перпендикуляра.
ü От точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
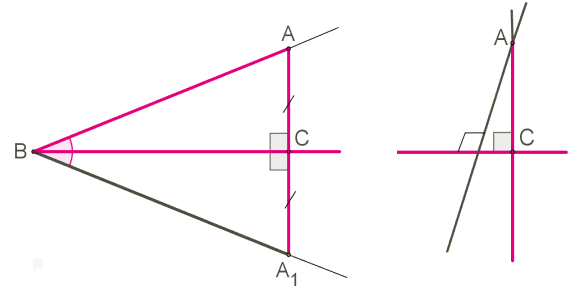Дано: ∡ABC.
Док-ть: что от точки A, не лежащей на прямой BC, можно провести
перпендикуляр к этой прямой.
Доказательство:
1. Отложим от луча BC угол, равный данному, и совместим эти углы накладыванием (представим, что сложим лист бумаги с равными углами по стороне BC).
Сторона BA совместится со стороной BA1.
При этом точка A наложится на некоторую точку A1.
Следовательно, совмещается угол ∡ACB с ∡A1CB.
Но углы ∡ACB и ∡A1CB — смежные, значит, каждый из них прямой.
2. Прямая AA1 перпендикулярна прямой BC, а отрезок AC является перпендикуляром от точки A к прямой BC.
Если допустить, что через точку A можно провести ещё один перпендикуляр к прямой BC, то он бы находился на прямой, пересекающейся с AA1. Но две к одной и той же прямой перпендикулярные прямые должны быть параллельны и не могут пересекаться.
Это противоречие, что означает: через данную точку к прямой можно провести только один перпендикуляр.
Медианы, биссектрисы и высоты треугольника
ü Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.
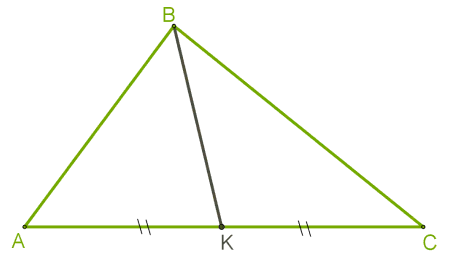
У треугольника три стороны, следовательно, можно построить три медианы.
· Все медианы пересекаются в одной точке.
ЗАРЯДКА ДЛЯ ГЛАЗ!!!https://pplisey1.my1.ru/_nw/9/82779615.jpg
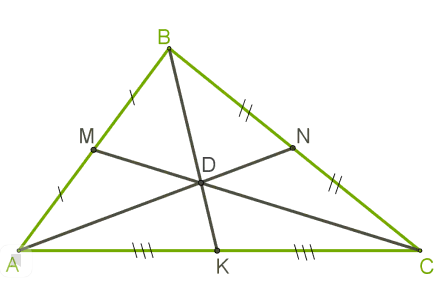
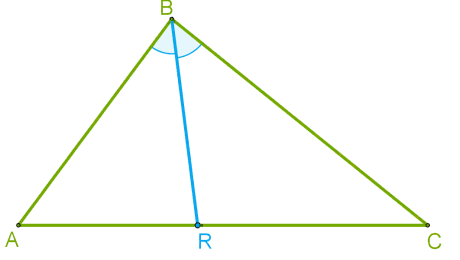
ü Биссектриса треугольника — это отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противоположной стороне.
Поэтому для построения биссектрисы необходимо выполнить следующие действия:
1. построить биссектрису какого-либо угла треугольника (биссектриса угла — это луч, выходящий из вершины угла и делящий его на две равные части);
2. найти точку пересечения биссектрисы угла треугольника с противоположной стороной;
3. соединить вершину треугольника с точкой пересечения на противоположной стороне отрезком — это и будет биссектриса треугольника.
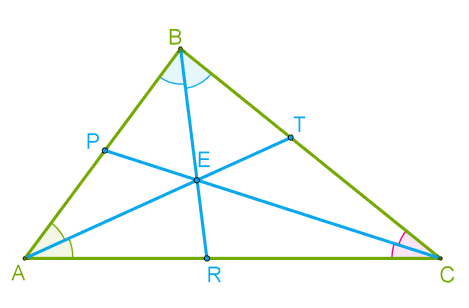
· Все биссектрисы пересекаются в одной точке.
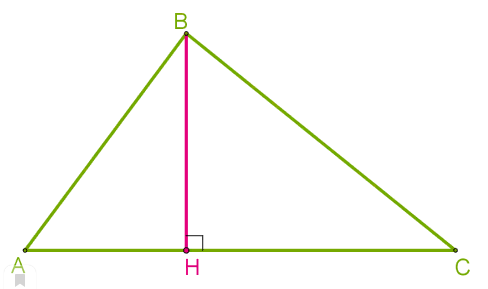
ü Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противоположную сторону.
Поэтому для построения высоты необходимо выполнить следующие действия:
1. провести прямую, содержащую одну из сторон треугольника (в случае, если проводится высота из вершины острого угла в тупоугольном треугольнике);
2. из вершины, лежащей напротив проведённой прямой, опустить перпендикуляр к ней (перпендикуляр — это отрезок, проведённый из точки к прямой, составляющей с ней угол 90°) — это и будет высота.
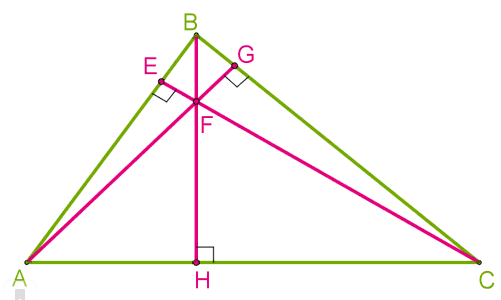
· Так же как медианы и биссектрисы, треугольник имеет три высоты.
· Высоты треугольника пересекаются в одной точке.
Обрати внимание!
Если из одной и той же вершины провести медиану, биссектрису и высоту, то медиана окажется самым длинным отрезком, а высота — самым коротким отрезком.
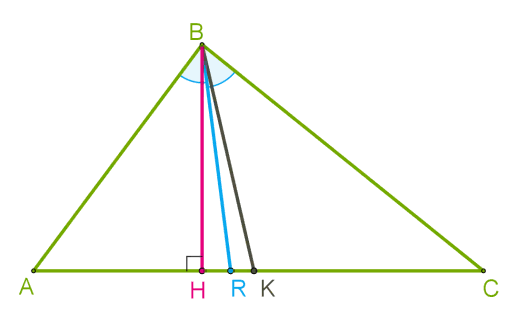
BH- высота BR- биссектриса BK-медиана
Модуль (практический)
Реши задачи!!! (с полным оформлением)
№ 1.
Дано: АС – биссектриса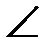 
А треугольника АВD.
Доказать: 
ВАС = DАС.
Доказательство:
Ч. и т.д.
№ 2. В треугольнике АСD проведены медианы АЕ, СВ и DF. Длины отрезков АF, ВD и СЕ соответственно равны 4 см, 3 см и 2 см. Найдите периметр треугольника АСD.
ЗАРЯДКА ДЛЯ ГЛАЗ!!!https://pplisey1.my1.ru/_nw/9/82779615.jpg
№ 3. DN – высота треугольника MNK; МD = DK. Доказать, что MND = KND.
Выполни и отправь учителю.
Сделать практическое задание № 101,102,103
обратная связь с учителем: Vk,
https://cloud.mail.ru/public/53fu/5zyz2NJ4n