Определение ускорения свободного падения
С ПОМОЩЬЮ ОБОРОТНОГО МАЯТНИКА
Цель: ознакомиться с закономерностями колебаний физического маятника, определить ускорение свободного падения.
Оборудование: оборотный (физический) маятник, секундомер.
Введение

Физическим маятником называется твердое тело, которое может качаться вокруг неподвижной горизонтальной оси. Точка 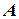 (рис. 1) – называется точкой подвеса маятника.
(рис. 1) – называется точкой подвеса маятника.
Получим выражение для периода качания физического маятника. Пусть маятник отклонили из положения равновесия на малый угол  , тогда изменение потенциальной энергии маятника равно
, тогда изменение потенциальной энергии маятника равно  , где
, где 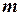 – масса маятника,
– масса маятника, 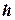 – высота, на которую поднялся центр масс
– высота, на которую поднялся центр масс  маятника над его самым нижним положением. Обозначая
маятника над его самым нижним положением. Обозначая 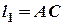 , получаем для изменения потенциальной энергии
, получаем для изменения потенциальной энергии
 .
.
В момент прохождения положения равновесия потенциальная энергия полностью переходит в кинетическую
 ,
,
где 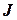 – момент инерции маятника относительно точки подвеса,
– момент инерции маятника относительно точки подвеса,  – его угловая скорость.
– его угловая скорость.
Будем пренебрегать силами трения и сопротивления движению тела, тогда сумма потенциальной и кинетической энергии остается неизменной
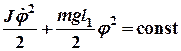 . (1)
. (1)
Дифференцируя равенство (1) по времени, получаем уравнение для малых колебаний физического маятника в виде
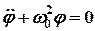 ,
,
где 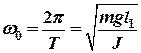 – частота,
– частота,  – период собственных колебаний.
– период собственных колебаний.
Частным случаем физического маятника является математический маятник – малое тело, подвешенное на невесомой нити. В этом случае вся масса маятника сосредоточена в точке  . Тогда
. Тогда  – длина (нити),
– длина (нити), 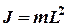 и получаем формулу для вычисления периода
и получаем формулу для вычисления периода
 . (2)
. (2)
Сравнивая выражения для периодов колебаний математического и физического маятников заключаем, что физический маятник колеблется с тем же значением периода, что и математический с длиной
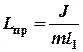 , (3)
, (3)
которая называется приведенной длиной физического маятника.
Согласно теореме Гюйгенса, если от точки 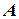 вдоль прямой
вдоль прямой  отложить отрезок, длина которого равна
отложить отрезок, длина которого равна 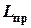 , и полученную точку
, и полученную точку  выбрать в качестве новой точки подвеса, то период колебаний физического маятник не изменится. Точка
выбрать в качестве новой точки подвеса, то период колебаний физического маятник не изменится. Точка  называется центром качания.
называется центром качания.
Теорема Гюйгенса используется для определения ускорения свободного падения с помощью оборотного маятника. Для этого определяют период колебаний маятника относительно точки 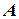 и находят сопряженную точку
и находят сопряженную точку  , для которой период колебаний такой же (период колебаний не изменяется при смене точки подвеса, поэтому маятник и называется оборотным). Расстояние между этими точками равно приведенной длине
, для которой период колебаний такой же (период колебаний не изменяется при смене точки подвеса, поэтому маятник и называется оборотным). Расстояние между этими точками равно приведенной длине 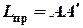 и может быть измерено точно. Поскольку период колебаний
и может быть измерено точно. Поскольку период колебаний 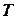 известен, то по формуле (3) можно вычислить
известен, то по формуле (3) можно вычислить 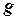 .
.
Описание установки
 Физический маятник – любое тело, имеющее ось вращения не проходящую через центр его масс. В нашем случае это стальная полоса 1 переменного сечения, на протяжении которой имеется несколько отверстий для крепления маятника на оси вращения. На одном конце полосы имеется отверстие 2, а на другом – ряд отверстий 3, расположенных на равном расстоянии друг от друга. Это позволяет получать физический маятник с различными периодами колебаний. Изменить положение центра масс маятника можно с помощью дополнительного груза 4.
Физический маятник – любое тело, имеющее ось вращения не проходящую через центр его масс. В нашем случае это стальная полоса 1 переменного сечения, на протяжении которой имеется несколько отверстий для крепления маятника на оси вращения. На одном конце полосы имеется отверстие 2, а на другом – ряд отверстий 3, расположенных на равном расстоянии друг от друга. Это позволяет получать физический маятник с различными периодами колебаний. Изменить положение центра масс маятника можно с помощью дополнительного груза 4.
Описание метода
Для физического маятника не удаётся измерить величины 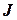 и
и 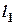 , необходимые для расчёта ускорения свободного падения
, необходимые для расчёта ускорения свободного падения 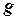 ,с той же точностью, что и период колебаний
,с той же точностью, что и период колебаний 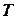 . Поэтому предлагается метод, позволяющий с помощью оборотного маятника исключить эти величины из расчётной формулы. Допустим, что удалось найти такое положение точки подвеса маятника, что его периоды колебаний одинаковы и равны
. Поэтому предлагается метод, позволяющий с помощью оборотного маятника исключить эти величины из расчётной формулы. Допустим, что удалось найти такое положение точки подвеса маятника, что его периоды колебаний одинаковы и равны 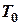 . Пусть
. Пусть  – расстояние от центра масс до новой точки подвеса, тогда обозначая расстояние между сопряженными точками
– расстояние от центра масс до новой точки подвеса, тогда обозначая расстояние между сопряженными точками  , из уравнения (2) получим расчётную формулу для ускорения
, из уравнения (2) получим расчётную формулу для ускорения 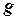 :
:
 . (4)*
. (4)*
Порядок выполнения работы
1. Повесить маятник на отверстие (2), расположенное вблизи конца полосы, как показано на рис. 2.
2. Отклонить маятник на малый угол (в пределах 5°–10°) от положения равновесия и отпустить. Измерив время 10 колебаний 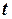 , определить период
, определить период 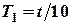 . Опыт повторить не менее пяти раз. Результаты записать в табл. 1
. Опыт повторить не менее пяти раз. Результаты записать в табл. 1
3. Снять маятник и измерить расстояния 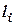 между отверстием (2) и отверстиями № 1–13. Результаты записать в табл. 2.
между отверстием (2) и отверстиями № 1–13. Результаты записать в табл. 2.
4. Повесить маятник на крайнее из отверстий (3). Измерить время 10 колебаний 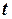 и определить период колебаний
и определить период колебаний 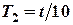 .
.
5. Перемещая ось каждый раз на одно отверстие, занести в табл. 2 периоды колебаний для всех отверстий.
Таблица 1 Перевернутый маятник Таблица 2
| № | 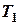 , с , с
|
 , с , с
|
| № | 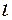 , м , м
|  , с , с
|
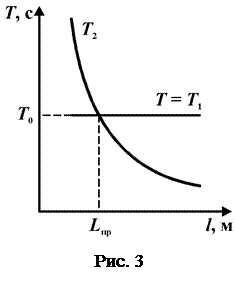
6. Построить на миллиметровой бумаге график (рис. 3) зависимости периода колебаний  от расстояния между осями
от расстояния между осями 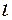 . Провести горизонтальную прямую, соответствующую периоду
. Провести горизонтальную прямую, соответствующую периоду 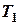 . Определить координаты
. Определить координаты 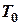 и
и 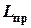 точки пересечения графиков.
точки пересечения графиков. 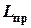 (приведенная длина маятника) и есть то самое расстояние между осями, при котором периоды колебаний оборотного маятника вокруг осей одинаковы и равны
(приведенная длина маятника) и есть то самое расстояние между осями, при котором периоды колебаний оборотного маятника вокруг осей одинаковы и равны  .
.
 7. Рассчитать среднее значение
7. Рассчитать среднее значение 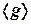 по формуле (4).
по формуле (4).
Примечание: для более точного определения положения точки пересечения и уменьшения погрешности расчета  рекомендуется построить вспомогательный рисунок. По табл. 2 найдем два соседних отверстия, для которых периоды качания
рекомендуется построить вспомогательный рисунок. По табл. 2 найдем два соседних отверстия, для которых периоды качания  и
и 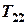 удовлетворяют неравенству
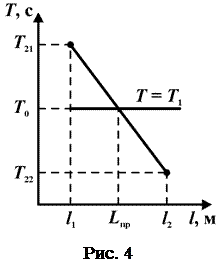
удовлетворяют неравенству  и построим график, состоящий из двух точек, на отдельном рисунке (рис. 4). Точка пересечения двух графиков находится между ними и может быть определена как точка пересечения двух прямых.
и построим график, состоящий из двух точек, на отдельном рисунке (рис. 4). Точка пересечения двух графиков находится между ними и может быть определена как точка пересечения двух прямых.
Для уменьшения погрешности можно измерить  и
и 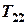 снова, по методике, указанной в п. 2.
снова, по методике, указанной в п. 2.
8. Оценить систематическую погрешность измерения 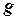 , используя аналогию дифференциала функции (3)
, используя аналогию дифференциала функции (3)  и погрешности
и погрешности 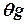 , (см. методы обработки результатов измерений):
, (см. методы обработки результатов измерений):
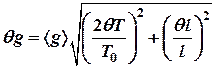 .
.
Погрешностью округления числа  пренебрегаем. Поскольку погрешность измерения
пренебрегаем. Поскольку погрешность измерения 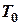 определяется графиком, то принять
определяется графиком, то принять 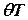 равной цене малого деления шкалы на графике, а
равной цене малого деления шкалы на графике, а 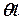 – цене деления линейки.
– цене деления линейки.
9. Записать результат в виде интервала
 .
.
10. Оценить отклонение найденной величины 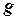 от табличного значения для Челябинска (
от табличного значения для Челябинска (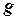 = 9,80 м/с2). Сделать вывод по работе.
= 9,80 м/с2). Сделать вывод по работе.