Энергетической характеристикой поля является потенциал. Электрическое поле неподвижных зарядов (электростатическое поле), поле постоянных токов (стационарное электрическое поле) являются потенциальными: потенциал не зависит от формы пути, по которому перемещается заряд из одной точки в другую. В электрической цепи переменного тока имеет место квазистационарное электрическое поле. Это позволяет охарактеризовать потенциальное электрическое поле в каждой его точке скалярной величиной, являющейся функцией координаты – потенциалом.
Потенциал любой точки электрического поля (точка " N ") численно равен работе сил поля по перемещению единичного положительного заряда из данной точки поля в точку, потенциал которой равен нулю (поверхность земли или бесконечно удалённая точка):
.
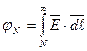Осуществляется нормирование потенциала на нуль в бесконечности.
Электрическое напряжение – есть работа сил поля по перемещению единичного положительного заряда (q = 1Кл) между точками поля:
.
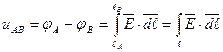Разность потенциалов (напряжение) есть физическая величина, равная линейному интегралу от вектора напряжённости потенциального поля взятому от одной точки к другой, и независящая от выбора пути интегрирования между этими точками.
Основной характеристикой электрического поля является вектор напряжённости. Для потенциального поля можно пользоваться скалярной характеристикой – потенциалом, как энергетической характеристикой.
В электрической цепи постоянного тока существует стационарное электрическое поле – в отличие от электростатического поля неподвижных зарядов. Оно поддерживается ЭДС источников энергии. Источник ЭДС непосредственно создаёт и поддерживает избыточные заряды, распределённые по проводнику. Заряды в свою очередь поддерживают стационарное электрич. поле. Эти избыточные заряды распределяются по поверхности проводов (не внутри!!!), а источник исключает самонейтрализацию.
Стационарное электрическое поле в отличие от электростатического создаётся и поддерживается источником ЭДС, и это поле существует не только в диэлектрике вокруг проводников, но и внутри проводников. Стационарное электрическое поле также как и электростатическое является потенциальным (в области вне источников ЭДС).
В электрической цепи переменного тока имеет место квазистационарное эл. поле, если скорость изменения электрического поля и длина линии невелики. Условием квазистационарности переменного тока (и создаваемого им поля) является требование, чтобы время распространения волны вдоль заданной длины провода было значительно меньше периода:
,
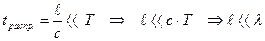где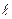 
- длина провода, с = 300 000 км/с - скорость света в вакууме; Т = 1/f - период изменения тока, l - длина волны (при f = 50 Гц Т = 0,02 с, l = 6 000 км).
МАГНИТНОЕ ПОЛЕ
Магнитное поле окружает движущиеся элементарные частицы, обладающие электрическим зарядом, и связано с ними. В проводнике с током и в пространстве вокруг него магнитное поле создаётся этим током.
Магнитное поле обнаруживается благодаря магнитным явлениям:
- притяжению или отталкиванию проводов с токами или намагниченных тел;
- действию проводника с током на магнитную стрелку;
- электромагнитной индукции.
В основе этих явлений лежит силовое действие магн. поля на движущиеся заряженные частицы. Силы взаимодействия магн. поля с движущимися заряженными частицами (токами) назыв-ся электромагнитными.
Интенсивность магнитного поля характеризуется вектором магнитной индукции 
. Магнитная индукция – векторная величина, характеризующая магнитное поле и определяющая силу, действующую на движущуюся частицу со стороны магнитного поля.
В численном выражении магнитная индукция равна отношению силы, действующей на заряженную частицу, к произведению заряда q и скорости частицы V, направленной так, чтобы эта сила была максимальна:
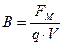, [В] = Тесла (Тл).
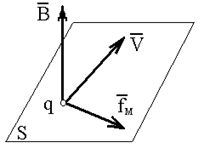Направление вектора магнитной индукции перпендикулярно векторам силы и скорости и совпадает с поступательным перемещением правого винта (буравчика), если вращать его в направлении от вектора силы к вектору скорости частицы с положительным зарядом.
Графически магнитное поле изображают с помощью линий магнитной индукции. Линию магнитной индукции проводят так, чтобы в каждой точке этой линии касательная к ней совпадала с вектором магнитной индукции.
Связь между магнитным полем и током выражается законом полного тока (для магнитного поля в вакууме):
.
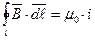Циркуляция вектора магнитной индукции вдоль произвольного замкнутого контура интегрирования пропорциональна полному току, охватываемому этим контуром (пронизывающему поверхность, ограниченную этим контуром).
Здесь: 
Гн/м – магнитная постоянная;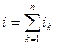 
- полный ток, охватываемый контуром интегрирования (алгебраическая сумма).
Если в магнитном поле выделить некоторую поверхность S, то через заданную поверхность будем иметь полный поток вектора магнитной индукции или магнитный поток:
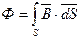, [Ф] = Вебер (Вб).
Магнитный поток есть поток вектора магнитной индукции, пронизывающий поверхность.
Таким образом, согласно формуле, магнитная индукция является плотностью магнитного потока в данной точке поля.