В отличие от нормального типа компоновки балочной конструкции, в которой балка настила располагается в плане перпендикулярно главным балкам, в усложнённом типе балочной конструкции балки настила располагаются параллельно главным балкам.
Толщину и пролёт настила в усложнённом типе балочной конструкции принимают по наиболее экономичному варианту нормального типа (см. табл.1)
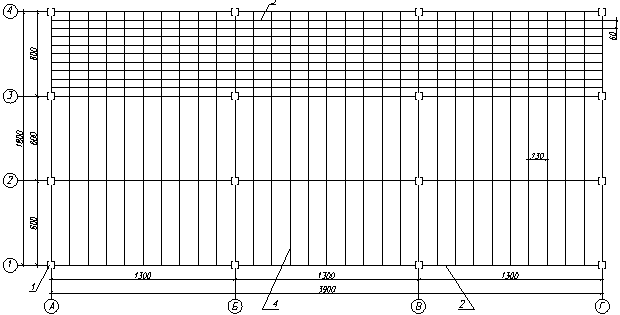
Рис.2. Схема балочной конструкции усложнённого типа:
1 – колонна, 2 – главная балка, 3 – балка настила, 4 – вспомогательная балка
В усложнённом типе компоновки балочной конструкции имеются вспомогательные балки и балки настила.
1. Расчёт балок настила
Пролёт балок настила принимается равным:
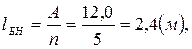
где n – число пролётов балок настила (см. рис. 2), n = 5.
Определим расчётную нагрузку на балку настила:
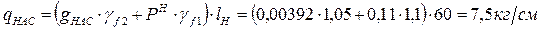 ,
,
g1HAC = t1∙γ = 0,5∙0,00785= 0,00392 кг/см2,
Определим расчётный изгибающий момент:

Определим требуемый момент сопротивления сечения балки:
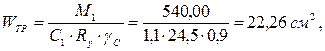
По требуемому моменту сопротивления сечения балки из сортамента подбирается ближайший двутавр, который будет иметь фактический момент сопротивления сечения балки – WФ. Принимаем двутавр № 10 с WФ = 39,7 см3.
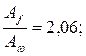
Тогда С1 = 1,04;
Проверим фактическое напряжение в балке настила:
 ,
,
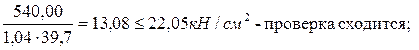
Уточним нормативную нагрузку, приходящуюся на балки настила:
 ;
;
Определим относительный прогиб балки настила:
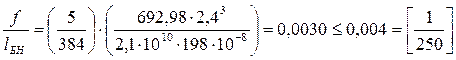
Результаты расчёта заносим в таблицу 2.
Таблица 2.
| № | Толщина настила t, мм | Вес 1 м2 настила gнас, кг/м2 | Пролёт lН, м | № двутавра | Вес 1м2 балочной конструкции, кг/м2 gнж=gнас+GБН/lН |
| 39,2 | 0,6 | 54,97 |
2. Расчёт вспомогательных балок
Определим нормативную нагрузку, действующую на вспомогательную балку:

Определим расчётную нагрузку, действующую на вспомогательную балку:
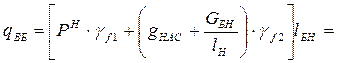
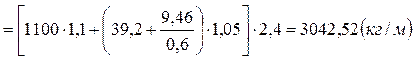
Здесь gНАС – вес 1 м2 экономичного варианта настила (см. табл. 1);
GБН – линейная плотность подобранного двутавра балки
настила для усложнённого типа компоновки балочной
конструкции.
Находим максимальный изгибающий момент:

Определяется требуемый момент сопротивления сечения вспомогательной балки:

Из сортамента подбираем ближайший номер двутавра.
Примем двутавр № 30Б1 с Wф = 427 cм3. Для подобранного двутавра определяем соотношение Аf /Аω:
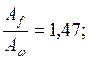
Тогда С = 1,056. Определяется С1 = 0,5(1+С) = 1,028.
Зоны чистого изгиба нет, так как нагрузки от балок настила на вспомогательную балку расположены настолько близко друг от друга, что их можно принять за равномерно распределенную нагрузку. Проверим напряжение во вспомогательной балке:
 ,
,
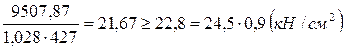 ;
;
Проверяется общая устойчивость вспомогательной балки:



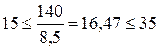
Затем найдём предельное отношение расчётной длины участка вспомогательной балки к ширине её пояса. Это отношение, если нет зоны чистого изгиба, находится по формуле:

где lef – расчётная длина участка вспомогательной балки,
lef = lH – bf = 600-140=460 мм;
b, t – соответственно ширина и толщина верхнего пояса
вспомогательной балки, b = 140 мм, t = 8,5 мм;
h – расстояние между центрами тяжести поясов вспомогательной балки, h = 296 мм;
bf – ширина верхнего пояса балки настила, bf = 140 мм.
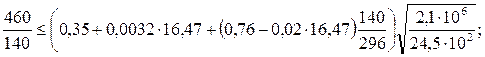
 .
.
Определим вес 1 м2 балочной конструкции усложнённого типа:

Полученные значения сравниваются с расходом металла для экономичного варианта нормальной компоновки балочной конструкции.
По результатам сравнения принимается экономичный вариант 68,68 кг/м2, т.е усложненный тип компоновки балочной конструкции.
Расчёт главной балки
Определим нагрузку, приходящуюся на главную балку:

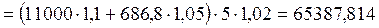 Н/м
Н/м
Здесь  - вес 1 м2 экономичного варианта балочной конструкции нормального типа.
- вес 1 м2 экономичного варианта балочной конструкции нормального типа.
Определим расчётный изгибающий момент:

Поперечная сила:
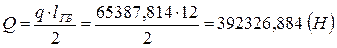 .
.
Определим требуемый момент сопротивления сечения главной балки:
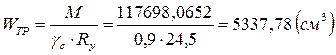 .
.
1). Подбор сечения главной балки:
Сечение главной балки принимается двутавровое из трёх листов, которые соединены между собой сварными швами. Для определения толщины стенки главной балки предварительно зададимся её высотой:
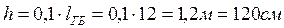
Определим толщину стенки:

Найденное значение толщины стенки уточняется и в дальнейших расчётах принимается с учётом толщин листов листовой стали.
Затем найдём оптимальную высоту главной балки:

где k =1,1 – коэффициент, учитывающий сварной вариант изготовления главной балки.
Из условия жёсткости определим минимальную высоту балки:
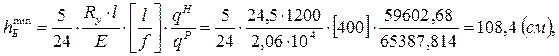
где [l/f] = 400 – обратная величина относительного прогиба;
qH – нормативная нагрузка на главную балку без учёта
коэффициента перегрузки;
qР – расчётная нагрузка.
Высота стенки должна назначаться из условия дискретности сортамента на листовую прокатную сталь.
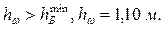
Определим толщину стенки главной балки из условия её работы на срез:
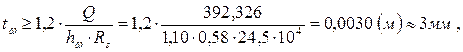
где Rs = 0,58 Ry. Принимаем tw=12 (мм).
При назначении высоты главной балки нужно учитывать сопряжения балок настила с главной балкой и сравнить полученный размер строительной высоты перекрытия с заданным размером.
Так как заданная строительная высота перекрытия hстр = 1,3 м, а полученная hстр = 1,14 + 0,005 = 1,145 м, то принимаем сопряжение балок настила с главной балкой в одном уровне.
Определим требуемый момент инерции балки:

Момент инерции стенки главной балки равен:
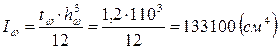
Определим момент инерции, приходящийся на пояса балки:
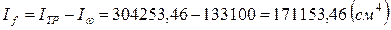
Балка принимается симметричного сечения. В таком случае требуемая площадь одного пояса равняется:
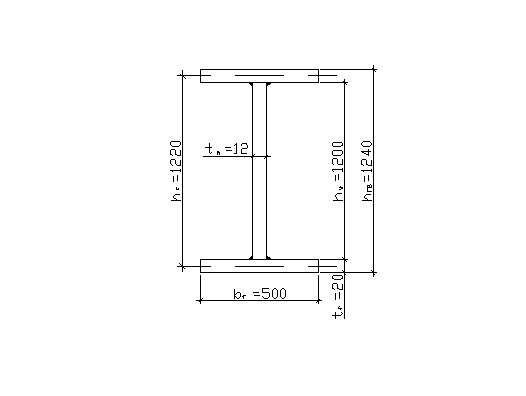
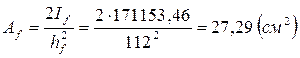
Рис.4. Сечение главной балки
По найденной площади пояса определяется ширина bf и толщина поясов tf из условия местной устойчивости сжатого пояса и общей устойчивости (см. таблицу 30 и п.7.22. приложения [1]):
Определим фактические значения: Jf и Wф;
bf = Af /Tf=27,29/2=13,65(см). Принимаем Bf=20 (См);
Wф=2Jтр/hб=2*304253,46/114=5337,78(см3)
hf=1,12(м); tf=0.02 (м); bf =0.200(м);
Пояса из универсальной стали: 0.200(м)*0.02(м),
bef / tf ≤ 0,11 hf/tw <0.5 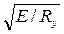 ;
;
bef = bf -tw/2=0.200-0.012/2=0.194(м)
9,7<10,27<14,6 => проверка выполняется.
Так как толщина и ширина листов пояса и стенки подбираются по сортаменту, то фактический момент сопротивления сечения главной балки отличается от требуемой. Поэтому необходимо проверить напряжение в подобранном сечении.
Определяем нормальное напряжение в середине пролета балки:
σ= Ммах/Wф ≤ RY γC:
σ=M/Wф= 1176,97/0,005337=220530,26 (кН/м2) 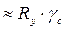 ;
;
RY =245000(кН/м2);
γC=0,9;
J=Jw + Jf=0.00133+0.002509=0,00384(м4);
Jf=2*bf*tf(hf/2)2=2*0,20*0.02(1,12/2)2=0.002509(м4);
Ммах=q*lгб2/8=(65,387*122)/8=1176,97(кН*м);
220530(кН/м2)< 220500(кН/м2).
проверка сходится (5% допускается).
Определим касательное напряжение на опорах балки:
τ=QS/(Jтр.tw) ≤ Rs γC,
Qмах=q*lгб/2=(65,387*12)/2=392,32(кН);
S=bftf(hw/2+tf/2)+twh2w/8=
=0,200*0,02(1,10/2+0,02/2)+0,012*1,12/8=0,00405(м3)
τ=392,32*0,00405/(0,00304253*0,012)=43531,39(кН/м2);
Rs=0,58 RY =142100(кН/м2);
43531,39 (кН/м2) <142100 (кН/м2);
проверка сходится.
2). Проверка общей устойчивости главной балки.
Устойчивость стенок балок на требуется проверять, если при выполнении условия п. 5.14 [1] условная гибкость стенки не превышает значения 3,5:

Поперечные рёбра жёсткости устанавливаются согласно требованиям п. 7.10 с учётом пп. 7.4 ÷ 7.9 [1].
Поперечные рёбра жёсткости делят балку на отсеки. Расстояние между поперечными рёбрами назначается в пределах
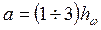
Принимаем а = 2,4 м.
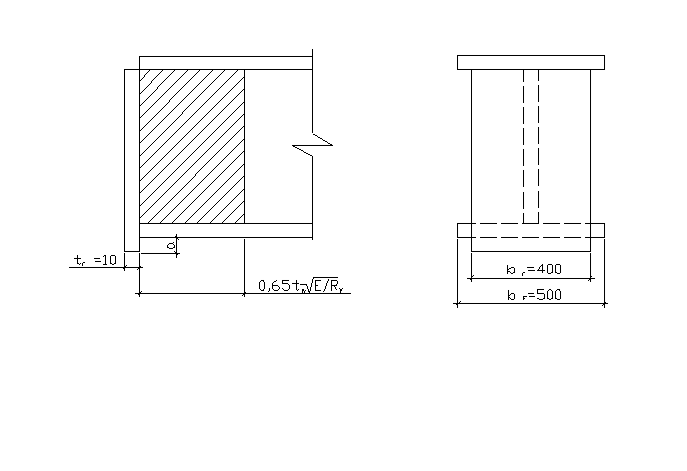
3). Расчёт опорного узла.
Рис.5. Опорный узел
Определим требуемую площадь опорного ребра из условия работы на смятие:
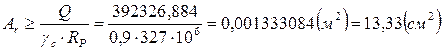
где RP – расчётное сопротивление выбранной марки стали смятию, находится по табл. 52 [1].
Ширина опорного ребра не должна быть меньше 180 мм и больше ширины пояса главной балки.
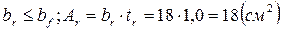
Толщина опорного ребра определяется в зависимости от требуемой площади ребра при работе на смятие.
Так как ребро к стенке главной балки крепится на сварке, то в работу опорного ребра на изгиб включается и часть стенки на длине

Определим площадь сечения опорного ребра, которая работает на изгиб:
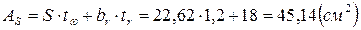
Определим напряжение изгиба в опорном ребре:
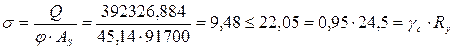
где φ = 91700, – коэффициент снижения напряжения при продольном изгибе, который определяется из табл.72 [1] в зависимости от гибкости ребра:
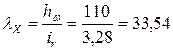
где ir – радиус инерции ребра:  ;
;
где Ix – момент инерции ребра:  ;
;
Определим катет сварного шва, соединяющего опорное ребро со стенкой главной балки:
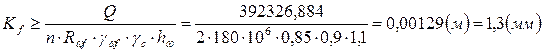 ,
,
где n = 2, – число сварных швов, воспринимающих опорную реакцию.
4). Расчёт узла сопряжения второстепенных балок с главной
Так как мы проектируем усложнённый вариант металлической балочной конструкции, то установим крепление второстепенных балок к ребру жёсткости главной балки болтами нормальной точности.
Из табл.58 [1] возьмём расчётные сопротивления болтов срезу:
Rbs = 190 МПа.
Из табл.59 [1] возьмём расчётные сопротивления болтов смятию:
Rbp = 495 МПа.
Коэффициент работы болтового соединения γb = 1 принимается по табл. 35 [1].
Предварительно назначим диаметр болтов db = 16 мм и диаметр отверстий для них d = 18 мм.
Несущая способность одного болта проверяется на срез и на смятие:
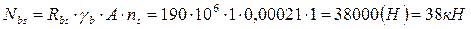
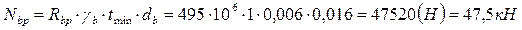
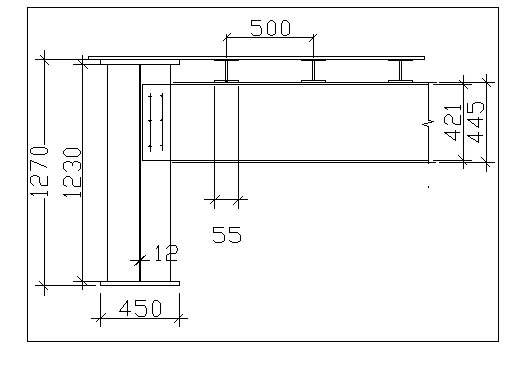
Рис.6. Крепление балок настила к главной балке
Определим усилие, которое воспринимают болты:

где Rоп – реакция опоры, которая равна:
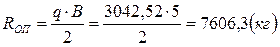
Определим число болтов:

Принимаем nБ = 3.
Определим площадь сечения стенки в ослабленном месте:

Проверим ослабленное сечение на действие поперечной силы:
