ТОЛЬЯТТИ 2000
Курсовая работа состоит из четырех заданий связанных между собой логически и охватывающих основные разделы курса
1. Расчет и выбор посадок;
2. Расчет гладких калибров;
3. Расчет размерных цепей;
4. Выбор измерительных средств
Составители: к.т.н. В.И. Пилинский;
доцент Ю.Н. Тальнов
Утверждено на заседании кафедры
«_3_» __апреля__2000 г.
1. НАЗНАЧЕНИЕ И СОДЕРЖАНИЕ КУРСОВОЙ РАБОТЫ
Курсовая работа предназначена для закрепления теоретических знаний, приобретенных студентами при изучении курса «Взаимозаменяемость, стандартизация и технические измерения» и выполняются студентами машиностроительного, технологического и автомобилестроительного факультетов специальности 1201, 1202.
Курсовая работа служит необходимым пособием студентам для самостоятельного решения современных инженерных задач, связанных с расчетом посадок, размерных цепей, выбором допусков деталей и калибров.
Курсовая работа состоит из четырех заданий, связанных между собой логически и охватывающих основные разделы курса: 1. Расчет и выбор посадок; 2. Расчет гладких калибров; 3. Расчет размерных цепей; 4. Выбор измерительных средств.
Курсовая работа состоит из расчетно-пояснителъной записки, в которую вшивается и графическая часть. Перечень чертежей приводится в задании на курсовую работу. Все чертежи выполняется карандашом на ватмане с соблюдением требований ЕСКД. Расчетно-пояснителъная записка содержит не более 20-25 страниц размером 297х210 мм, написанных от руки. Разрешается заполнение обеих сторон листа.
2. РАСЧЕТ И ВЫБОР ПОСАДОК
Целью данного этапа является овладение студентами методами расчета и выбора посадок гладких сопряжении.
Рассчитать посадку означает по заданным эксплуатационным требованиям к работе сопряжения определить значения допусков вала и отверстия и расположение полей допусков относительно нулевой линии.
2.1 Расчет подвижной посадки
Подвижной называют посадку, в которой гарантировано появление зазора при любом сочетании предельных размеров сопрягаемых деталей. Схема расположения полей допусков подвижной посадки показана на рис.1. Как видно,
TS = TD + Td = Smax – Smin , (2.1)
TS =0,124мм-0,040мм=0,084мм
где TD и Td – допуски отверстия и вала;
Smax и Smin – максимальный и минимальный зазоры;
TS – допуск посадки.
Для инженерных расчетов величину · можно определить следующим образом:
 . (2.2)
. (2.2)
По ближайшему меньшему табличному (табл. 2.1) значению · находим квалитет.
Таблица 2.1
| Квалитет | IT5 | IT6 | IT7 | IT8 | IT9 | IT10 | IT11 | IT12 | IT13 | IT14 | IT15 | IT16 | IT17 |
| Значения |
Так как (рис.1) верхнее отклонение поля допуска вала /es/ равно минимальному зазору 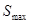 , то исходя из этого можно определить поле допуска вала, выбрав его по таблицам СТ СЭВ 145-75 [1].
, то исходя из этого можно определить поле допуска вала, выбрав его по таблицам СТ СЭВ 145-75 [1].
Расчет подвижной посадки
Задано: номинальный размер сопряжения  мм: максимальный и минимальный зазоры
мм: максимальный и минимальный зазоры  мкм,
мкм,  мкм, сопряжение выполнено в системе отверстия () и при этом Td=TD. Выбрать посадку.
мкм, сопряжение выполнено в системе отверстия () и при этом Td=TD. Выбрать посадку.
По формуле (2.11) подсчитываем величину а:
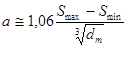 .
.

По табл. 2.1. определяем, что ближайшим меньшим является квалитет IT8 для которого атабл = 25.
По таблицам СТ СЭВ 145-75 находим, что для IT8 = 40 мкм.
По таблицам СТ СЭВ 145-75 находим, далее, что ближайшим значением |es| к Smin = 40 мкм является |es| табл. = 40 мкм. Это соответствует полю допуска вала е7. Следовательно, в результате расчета получена посадка &90Н8/е8, для которой Smin табл.=40 мкм и Smах табл.=106 мкм. После расчета посадки следует вычертить схему расположения полей допусков с указанием предельных размеров, зазоров и отклонений (см. рис.2).
2.2 Расчет переходной посадки
Переходные посадки используются для центрирования сопряжений и характеризуются малыми зазорами и натягами, что, как правило позволяет производить сборку при небольших усилиях (вручную или при помощи молотка).
Выбор переходных посадок определяется требуемыми точностью центрирования и легкостью сборки и разборки сопряжения. Первое из требований определяет максимальный допустимый зазор при заданном предельном значении Ео радиального биения втулки на валу. Расчетное соотношение имеет вид:
Smах расч. 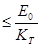 , (2.11)
, (2.11)
где КТ = 2…5 – коэффициент запаса точности, учитывающий погрешности формы и расположения поверхностей сопрягаемых деталей, их износ и снятие неровностей при переборках.
Степень легкости сборки и разборки сопряжения с переходной посадкой определяется вероятностью Ps получения в ней зазора, которая определяется из соотношения (2.12) в предположении, что рассеяние зазоров (натягов) подчиняется закону нормального распределения:
Ps= 0,5Фo(Zs), (2.12)
где Фo(Zs) – функция Лапласа.
Определим значение Фo(Zs)=Ps–0,5, а затем по таблице (приложение 1) вычислим значение аргумента Zs. Тогда величину минимального расчетного зазора определим [2] по формуле:
Smin расч. = Smах расч.  (2.13)
(2.13)
Пользуясь таблицами СТ СЭВ 145-75 следует подобрать посадку так, чтобы удовлетворялись следующие условия:
Smах табл. £ Smах расч.; Smin табл. á Smin расч.
Переходные посадки образуются, главным образом, сочетанием полей допусков валов Is, K, m, и n c основными отверстиями или полей допусков отверстий Js, K, M, N с основными валами. При этом переходные посадки применяются в квалитетах, не грубее JT8.
Выбранная посадка должна обеспечивать вероятность получения зазора в пределах заданного (допускается применение посадки, у которой расчетная величина вероятности зазора меньше заданной, но не более чем на 20%, если за единицу или 100% принять заданное значение Ps).
Рекомендуемые значения Ps для получения требуемых условий сборки приведены в табл. 2.2.
Таблица 2.2.
| Степень легкости сборки сопряжения | Сборка осуществляется | |||
| Часто и вручную | Нечасто и с применением молотка | Нечасто и со значительными усилиями | Нечасто и с использованием пресса | |
| Вероятность появления зазора в %. | 0,5 |
В первом приближении номер квалитета можно определить по следующей формуле:
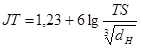 , (2.14)
, (2.14)
где TS – допуск посадки.
Расчет переходной посадки
Требуется подобрать переходную посадку для установки зубчатого колеса на вал при следующих условиях: номинальный диаметр сопряжения dH = 50мм,степень кинематической точности зубчатого колеса – 9 (радиальное биение по СТ СЭВ 641-77 Ео = 130 мкм.), вероятность получения зазора – Ps = 20%. Коэффициент КТ = 2.
Максимальный зазор будет равен (формула (2.11)):
Smах расч. 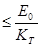 ,
,
Smах расч. 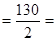 65 мкм
65 мкм
По формуле (2.12) определяем вначале значение функции Лапласа, а затем по таблице (приложение 1) находим величину аргумента Zs.
Фо(Zs) = Ps - 0,5 = 0,2 - 0,5 = - 0,3; Фо(-Zs) =- Фо(Zs), то Zs = - 0,841.
Величину минимального зазора определяем по формуле (2.13):
Smin расч. = Smах расч. 
Smin расч 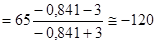 мкм.
мкм.
Знак “ - “, полученный при Smin расч, свидетельствует о том, что это не зазор, а натяг.
Находим согласно (2.1) допуск посадки
TS=Smax–Smin=65–(–120)=185мкм.
Далее, по формуле (2.14) рассчитываем номер квалитета:
 ,
,

При дробном значении номера JT часто, но не всегда, принимается равноточное сопряжение: квалитет отверстия выбирается большим, чем квалитет вала. Рассматриваемому примеру удовлетворяет посадка а.?

системе отверстия
Среднее квадратичное отклонение посадки 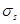 определяем по формуле (2.3):
определяем по формуле (2.3):
 мкм
мкм
Для расчета вероятности распределения зазоров или натягов найдём среднее их значение  :
:
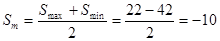 мкм
мкм
Знак минус указывает на то, что средним является натяг и, следовательно, в собранных спряжениях будет в основном появляться натяг величиной 10 мкм.
Далее необходимо рассчитать вероятность появления зазоров и натягов в процентах от количества собранных спряжений:
Находим значение функции. Лапласа, имея в виду, что

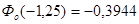
По формуле (2.12) для посадки 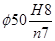 находим, что
находим, что  или 10% (это вероятность появления зазоров). Таким образом, большинство спряжений (89,44%) будет иметь натяг.
или 10% (это вероятность появления зазоров). Таким образом, большинство спряжений (89,44%) будет иметь натяг.
В завершение вероятностного расчета необходимо построить диаграмму процентного соотношения зазоров и натягов (рис. З). Построение кривой нормального распределения делается по функции плотности вероятностей. Для этого по горизонтальной оси откладывается отрезки равные среднему квадратичному отклонению посадки  в пределах
в пределах 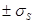 . На оси ординат в произвольном масштабе откладываются отрезки
. На оси ординат в произвольном масштабе откладываются отрезки  , соответственно значения
, соответственно значения  и
и  , приведённым в табл. 2.3.
, приведённым в табл. 2.3.
Таблица 2.3
Параметр 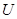
| 0,0 | 0,5 | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 |
Ордината 
| 1,00 | 0,88 | 0,60 | 0,33 | 0,14 | 0,04 | 0,0 |
Через полученные точки с помощью лекала проводится плавная кривая. После расчёта посадки построить схему расположения полей допусков.
2.3 Расчет неподвижной посадки
Неподвижная (с гарантированным натягом) посадка считается годной, если при неподвижном натяге гарантируется неподвижность сопряжения, а пря максимальном - прочность соединяемых деталей. При этих условиях сопряжение будет передавать заданную нагрузку (крутящий момент или ocевую силу, либо то и другое), а детали будут выдерживать без разрушения напряжения, вызванные натягом. Сопряжение с неподвижной посадкой показано на рис. 4.
Минимальный расчетных натяг 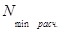 определяется так:
определяется так:
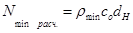 , (2.15)
, (2.15)
где  - минимальное давление, возникающее на контактной поверхности, вала и втулки,
- минимальное давление, возникающее на контактной поверхности, вала и втулки, 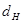 - номинальный (рис.4) размер сопряжения,
- номинальный (рис.4) размер сопряжения, 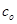 - коэффициент, определяемые во формуле:
- коэффициент, определяемые во формуле:
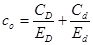
Здесь 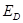 и
и 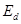 - соответственно модули-упругости материалов втулки, и вала;
- соответственно модули-упругости материалов втулки, и вала; 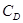 и
и 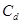 - коэффициенты, рассчитываемые по формулам:
- коэффициенты, рассчитываемые по формулам:
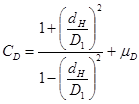 ;
;  ,
,
где 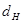 ,
, 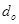 ,
,  - геометрические размеры деталей сопряжения (рис.4);
- геометрические размеры деталей сопряжения (рис.4); 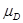 и
и 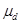 - соответственно коэффициенты Пуассона для материалов втулки и вала.
- соответственно коэффициенты Пуассона для материалов втулки и вала.
Значение модулей упругости и коэффициентов Пуассона можно брать из табл. 2.4.
Таблица 2.4
| Материал | Модуль упругости Е, Па | Коэффициент Пуассона |
| Сталь | 2,1*1011 | 0,30 |
| Чугун | 0,9*1011 | 0,25 |
| Бронза | 1,12*1011 | 0,33 |
| Латунь | 1,05*1011 | 0,33 |
Минимальное давление рассчитывается следующим образом:
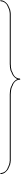
 ;
;
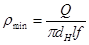 ; (2.16)
; (2.16)
 ;
; 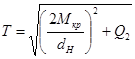
где 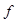 ,
, 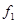 ,
, 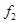 - коэффициенты трения, возникающие на контактной поверхности (в первом приближении их можно принимать равными);
- коэффициенты трения, возникающие на контактной поверхности (в первом приближении их можно принимать равными);
l – длина запрессовки (рис.). Указанные три разновидности формулы (2.16) предназначены для расчёта  , при нагружении сопряжения соответственно крутящим моментом, осевой силой, а также тем и другим совместно.
, при нагружении сопряжения соответственно крутящим моментом, осевой силой, а также тем и другим совместно.
Максимальный расчётный натяг 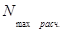 находится:
находится:
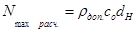 (2.17)
(2.17)
где допустимое значение  находится, исходя из требования к прочности сопрягаемых деталей. Опыт показывает, что обычно лимитирующей деталью является втулка (отверстие). Тогда величину
находится, исходя из требования к прочности сопрягаемых деталей. Опыт показывает, что обычно лимитирующей деталью является втулка (отверстие). Тогда величину  можно рассчитать по формуле:
можно рассчитать по формуле:
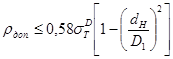 (2.18)
(2.18)
Проверку прочности вала можно (если это необходимо) выполнить по формуле:
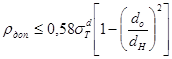 (2.19)
(2.19)
В формулах (2.18) и (2.19)  и
и  - соответственно пределы текучести материалов втулки и вала. Значения
- соответственно пределы текучести материалов втулки и вала. Значения 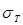 для некоторых конструкционных материалов даны в табл.2.5.
для некоторых конструкционных материалов даны в табл.2.5.
Таблица 2.5.
| Марка материала | 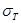 , Па , Па
| Марка материала | 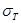 , Па , Па
| Марка материала | 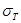 , Па , Па
|
| Сталь 20 | 274*106 | Бронза ОФ10-1 | 140*106 | Латунь ЛКС80-3-3 | 140*106 |
| Сталь 30 | 294*106 | Бронза ОЦ10-2 | 180*106 | Латунь ЛН56-3 | 160*106 |
| Сталь 35 | 314*106 | Бронза ОФ05-0,4 | 240*106 | Латунь ЛК80-3 | 200*106 |
| Сталь 40 | 333*106 | Бронза БрАНц9-2 | 300*106 | Латунь Л050-1 | 420*106 |
| Сталь 45 | 353*106 | Бронза БрЖ9-4 | 350*106 | Латунь Л059-1 | 450*106 |
| Чугун Сч28-48 | 275*106 | Бронза БрХО5 | 400*106 | Латунь Л0562-2 | 500*106 |
| Бронза БрОЦ4-3 | 65*106 | Латунь Л090-1 | 85*106 | Латунь Л060-1 | 560*106 |
| Бронза БрОСЦ5-5-5 | 100*106 | Латунь Л62 | 110*106 | Латунь Л070-1 | 600*106 |
Для нахождения табличных натягов  и
и 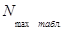 , следует воспользоваться следующими выражениями:
, следует воспользоваться следующими выражениями:
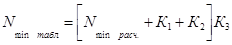 ; (2.20)
; (2.20)
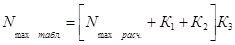 ;
;
где 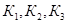 - поправочные коэффициенты.
- поправочные коэффициенты.
Поправочный коэффициент 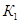 зависит от шероховатости сопрягаемых поверхностей вала (
зависит от шероховатости сопрягаемых поверхностей вала ( ) и втулки (
) и втулки (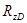 ):
): 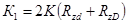
В свою очередь поправочный коэффициент 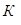 выбирается [3] из табл. 2.6.
выбирается [3] из табл. 2.6.
Таблица 2.6
| Метод сборки сопряжения | Коэффициент 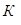
|
| Механическая запрессовка без смазки | 0,25 ÷ 0,50 |
| Тоже с мазкой | 0,20 ÷ 0,35 |
| С нагревом втулки | 0,40 ÷ 0,50 |
| С охлаждением вала | 0,60 ÷ 0,70 |
Поправочных коэффициент 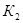 учитывает действие центробежных, сил снижающих прочность сопряжения, и составляет 1÷4 мкм, если
учитывает действие центробежных, сил снижающих прочность сопряжения, и составляет 1÷4 мкм, если 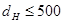 мкм скорость вращения узла не превышает 30 м/с [3].
мкм скорость вращения узла не превышает 30 м/с [3].
Поправочный коэффициент  , зависит от изменения контактного давленая в связи с ростом отношения
, зависит от изменения контактного давленая в связи с ростом отношения 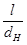 и выбирается [3] по табл. 2.7.
и выбирается [3] по табл. 2.7.
Таблица 2.7.
Отношение 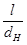
| Отношение диаметров 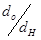
| ||
| 0 ÷ 0,2 | 0,3 ÷ 0,7 | 0,8 ÷ 0,9 | |
| 0,2 | 0,46 ÷ 0,52 | 0,42 ÷ 0,45 | 0,57 ÷ 0,62 |
| 0,4 | 0,73 ÷ 0,76 | 0,75 ÷ 0,80 | 0,80 ÷ 0,84 |
| 0,6 | 0,82 ÷ 0,85 | 0,84 ÷ 0,87 | 0,86 ÷ 0,90 |
| 0,8 | 0,84 ÷ 0,86 | 0,86 ÷ 0,88 | 0,87 ÷ 0,93 |
| 1,0 | 0,86 ÷ 0,88 | 0,88 ÷ 0,91 | 0,90 ÷ 0,95 |
Расчет неподвижной посадки
Рассчитать и выбрать посадку в системе отверстия для установки червячного колеса на ступицу. Номинальный диаметр сопряжения  мм; длина сопряжения
мм; длина сопряжения  мм; отношение
мм; отношение  ; материал ступицы – сталь 18ХГМ; материал червячного колеса (обода) – сталь 40ХН; высота микронеровностей
; материал ступицы – сталь 18ХГМ; материал червячного колеса (обода) – сталь 40ХН; высота микронеровностей 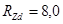 мкм и
мкм и  мкм; наружный диаметр колеса
мкм; наружный диаметр колеса  мм; диаметр отверстия на валу (ступица)
мм; диаметр отверстия на валу (ступица)  мм; прессование производится на прессе со смазкой; коэффициент трения
мм; прессование производится на прессе со смазкой; коэффициент трения 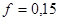 ; крутящий момент, передаваемый сопряжением,
; крутящий момент, передаваемый сопряжением, 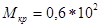 Н*м.По табл. подбираем необходимые значения параметров и поправочных коэффициентов:
Н*м.По табл. подбираем необходимые значения параметров и поправочных коэффициентов: 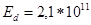 Па;
Па; 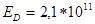 Па;
Па; 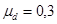 ;
; 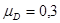 ;
; 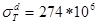 Па;
Па;  Па;
Па; 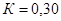 ;
;  мкм;
мкм; 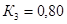
Подсчитываем значения коэффициентов 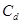 ,
, 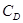 и
и 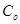 :
:
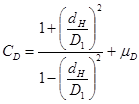 ;
;  ,
,
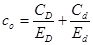
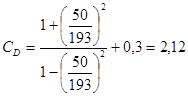 ;
;  ;
;  1/Па
1/Па
По формулам (2.15) и (2.16) находим величину 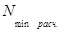 :
:
 ,
,  ;
;
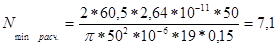 мкм
мкм
Определяем значение поправочного коэффициента 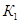 :
:
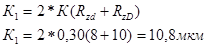
По формуле (2.20) рассчитываем величину:

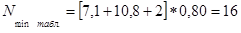 мкм.
мкм.
По формулам (2.18) и (2.17) находим значения  и
и 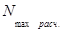
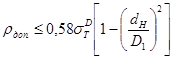
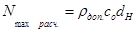
 мкм
мкм
Находим далее, по формуле (2.20) величину 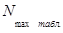 :
:
 ;
;
 мкм
мкм
Принимая теоретико-вероятностный метод, по формуле (2.6) рассчитываем значение допусков вала Td и втулки TD (подставляя в (2.6) вместо зазоров натяги).
 мкм
мкм
По таблицам от СТ СЭФ 145-75 подбираем, что ближайшим меньшим оказывается допуск Td=TD=98 мкм, что соответствует квалитету IT10(несмотря что по расчетам получился 10 квалитет я могу взять только 8). Из схемы (рис. 4) находим, что нижнее отклонение поля допуска вала
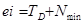
2.2 Расчет и построение полей допусков предельных калибров
Допуски и их расположение рабочих и контрольных калибров регламентированы стандартом СТ СЭВ 157-75 «Калибры гладкие для размеров до 50 мм». Для контроля отверстий применяются калибры-пробки, а для контроля вала - калибры-скобы. С конструкциям калибров следует ознакомиться в справочнике [4]. По назначению калибры делятся на рабочие, приёмные и контрольные (контркалибры).
Рабочие калибры (проходной Р-ПР, непроходной Р-НЕ) предназначены для контроля размеров деталей в процессе их изготовления. Этими калибрами пользуются на рабочих местах.
Приёмными калибрами П-ПР и П-НЕ пользуется представитель заказчика при выборочном инспекционном контроле деталей.
Контрольные калибры K-ПP и К-НЕ и К-И предназначены для контроля размеров рабочих калибров-скоб. Контроль рабочих калибров-скоб производится универсальными измерительными средствами.
При построении схемы полей допусков калибров (рис.5) необходимо знать, что номинальными размерами, от которых откладываются отклонения, для калибров служат предельные размеры деталей. Следовательно, для проходного калибра-пробки отклонения откладываются от наименьшего предельного размера отверстия  , а для непроходного калибра-пробки – от наибольшего предельного размера
, а для непроходного калибра-пробки – от наибольшего предельного размера  . Для калибра-скобы размеры проходной стороны от
. Для калибра-скобы размеры проходной стороны от 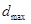 вала, а непроходной -
вала, а непроходной -  вала. Поле допуска проходного калибра состоит из двух частей: на изготовление и на износ, поскольку в процессе контроля проходная сторона калибра должна полностью проходить на всю длину контролируемой детали. Для непроходных калибров, изнашивающихся незначительно в процессе контроля, устанавливают лишь допуск на его изготовление.
вала. Поле допуска проходного калибра состоит из двух частей: на изготовление и на износ, поскольку в процессе контроля проходная сторона калибра должна полностью проходить на всю длину контролируемой детали. Для непроходных калибров, изнашивающихся незначительно в процессе контроля, устанавливают лишь допуск на его изготовление.
При построении полей допусков калибров по таблицам СТ СЭВ157-75 определить отклонение середины поля допуска на изготовление проходного калибра: для отверстия (координата Z) относительно наименьшего предельного размера, а для вала (координата Z1) относительно наибольшего предельного размера. Для отверстия диаметром 32 мм квалитета JT7 Z = 3,5 мкм, а для вала того же размера и квалитет JT6 Z1 = -3,5 мкм. Допуски на изготовление калибров Р-ПР и Р- (см. таблицы СТ CЭB 157-75) равны: для калибров – пробок – Н = 4 мкм, а для калибров – скоб – Н1 = 4 мкм. Значения половин допусков для проходных калибров отложить симметрично относительно осей Z и Z1, а для непроходных калибров – относительно наибольшего предельного размера отверстия для пробки и наименьшего предельного размера вала для скобы.
Значения верхнего ES(es)k и нижнего EJ(ei)k отклонения калибров Р-ПР на изготовление относительно номинальных размеров определяются следующим образом:
 ;
;  ;
;  ;
; 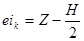
В рассматриваемом примере (рис.5) они равны: для калибра-пробки esk = 3,5 + 2 = 5,5 мкм, eik = 3,5 – 2 = 1,5 мкм; для калибра – скобы
ESk = - 3,5 + 2 = 1,5 мкм, EJk = - 3,5 – 2 = - 5,5 мкм.
Определим границы износа калибров у и у1, которые в данном случае для проходной пробки и скобы соответственно равны:
у = - 3 мкм и у1 = 3 мкм. Величины допусков на износ калибров будут составлять по 4,5 мкм. По таблицам CT СЭВ 157-75 необходимо определить также значение допусков на изготовление калибров K-И и построить поля их допусков, руководствуясь схемой, приведенной в этом стандарте.
Подсчитать исполнительные размеры калибров по формулам, представленным в таблицах стандарта СТ СЭВ 157-75. Исполнительным называется размер, проставленный на рабочем чертеже калибра.
Для калибра – пробки.
 мм.
мм.
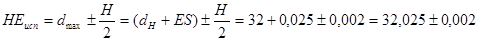 мм.
мм.
Для калибра – скобы.
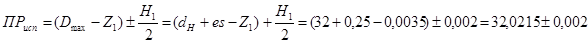 мм
мм
 мм.
мм.
Для контрольных калибров.
 мм;
мм;
 мм;
мм;
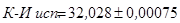 мм.
мм.
2.5 Общие указания и рекомендации по расчету посадок и калибров
2.5.1 Исходные данные для расчета подвижной переходной и неподвижной посадок гладких сопряжений, а также посадки подшипника качения задаются каждому студенту и помещаются в бланке – задании к курсовой работе (см. форму 2).
2.5.2 Конкретное сопряжение, используемое для расчета посадок, также указывается в бланке – задании в виде названия сопряжения (например, вал – шестерня, вал – шкив, ступица – обод червячного колеса и т.д.).
2.5.3 Для расчета калибров в бланке – задании указывается конкретное сопряжение по образцу п. 2.5.2.
2.5.4 По описанной части курсовой работы вычерчиваются схемы, показанные на рис. 1-5, но применительно к рассчитанным (или выбранным) данным
2.5.5 Все расчеты следует производить в Международной системе физических величин, руководствуясь при этом стандартом СТ СЭВ 1052 – 78 [5].
3. РАСЧЕТ РАЗМЕРНЫХ ЦЕПЕЙ
Цель расчета. Исходя из служебного назначения и условий работы узла или механизма научиться составлять и рассчитывать размерные цепи.
3.1 Общие указания по составлению размерных цепей
Размерной цепью (по ГОСТ 1639-70) называется совокупность размеров, образующих замкнутый контур и участвующих в решении поставленной задачи. Задачи, которые решаются с помощью размерных цепей, могут быть конструкторскими (выбор размеров и точности звеньев), технологическими (обеспечение заданного зазора при сборке), настроечными (наладка станков), связанными с выполнением технических измерений и другими. Размерные цепи бывают различных видов в зависимости от назначения (конструкторские, технологические, измерительные), характера взаимного расположения звеньев (линейные, угловые, плоские, пространственные), принадлежности к детали или узлу (подетальные, сборочные) и др.
Размерные цепи состоят из звеньев, в качестве которых могут быть размеры деталей, зазоры и натяги. Различают несколько видов звеньев. Исходное звено – это звено, возникающее в результате постановки задачи при проектировании, для решения которой используется размерная цепь (например, обеспечить заданную параллельность стола станка к оси шпинделя). Замыкающее звено – это звено, получаемое в размерное цепи последним в результате решения поставленной задачи, том числе при изготовлении, сборке и измерении. Составляющее звен о - это звено размерной цепи, изменение которого вызывает изменение исходного или замыкающего звена. Составляющие звенья делятся на увеличивающие и уменьшающие. Увеличивающее звено – это составляющее звено, с увеличением которого увеличивается исходное или замыкающее звено. Уменьшающее звено – это звено, с увеличением которого уменьшается исходное или замыкающее звено.
Одно из составляющих звеньев при необходимости может быть принято в качестве компенсирующего звена. Компенсирующее звено – это предварительно выбранное составляющее звено, изменением которого достигается требуемая точность замыкающего звена.
При решении размерных цепей возникают два вида задач: (первая и вторая).
Первая задача заключается в определении номинального размера, допуска и предельных отклонений замыкающего звена по заданным номинальным размерам, допускам и отклонениям составляющих звеньев. Эта задача чаще всего встречается при расчетах технологических процессов или как проверочная при конструировании деталей и узлов машин.
Вторая задача заключается в определение величины допуска и отклонений составляющих звеньев по заданным номинальным размерам всех звеньев цепи и заданным предельным размерам замыкающего звена. Данная задача типична для конструкторских расчетов.
Следует иметь в ввиду, что в литературе можно встретить название
указанных задач как прямая и обратная.
Существует ряд методов расчета размерных цепей:
а) метод полной взаимозаменяемости;
б)метод неполной взаимозаменяемости (теоретико-вероятностный);
в) метод ограниченной взаимозаменяемости (группового подбора).
Введем условные обозначения параметров цепи. Номинальные размеры составляющих увеличивающих звеньев – А1, А2, … Аi; уменьшающих – A3’, A4’, … Aj’.
Номинальный размер замыкающего звена - АD. Допуски составляющих звеньев – TA1, TA2, TA3, TAi, TAj. Допуск компенсирующего звена – Тк. Верхнее и нижнее отклонения замыкающего звена - ESD, EJD (или esD и eiD). Верхние отклонения составляющих звеньев – ESA1, ESA2, ESA, (eSAi, eSA и т.д.). Нижние отклонения составляющих звеньев - EJA1, EJA2, EJA3 (eiA1, eiA2 и т.д.). верхнее и нижнее отклонения компенсирующего звена - ESk (esk) и EJk (eik).
3.2 Решение первой задачи
В современном машиностроение, особенно, серийном и массовом наиболее часто находят применение теоретико-вероятностный метод расчета размерных цепей, обеспечивающий наиболее экономичное решение технологических и конструкторских задач. Поэтому в курсовой работе используется именно данный метод решения размерных цепей.
При массовом или крупносерийном производстве, особенно в многозвенных размерных цепях, вероятность одновременного попадания на сборку, например, наибольших размеров всех уменьшающих звеньев чрезвычайно мала. Поэтому размерные цепи целесообразно рассчитывать вероятностным методом, позволяющим без расширения поля допуска замыкающего звена расширить поля допусков на изготовлении составляющих звеньев.
Номинальный размер замыкающего звена рассчитывается так:
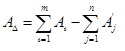 , (3.1)
, (3.1)
где m и n - число увеличивающих и уменьшающих звеньев в цепи.
Допуск замыкающего звена рассчитывается следующим образом:
 (3.2)
(3.2)
Значение координаты середины поля допуска замыкающего звена рассчитывается следующим образом:
 (3.3)
(3.3)
В свою очередь координаты середин полей допусков увеличивающих и уменьшающих звеньев рассчитываются соответственно так:
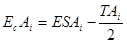 или
или  ; (3.4)
; (3.4)
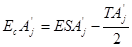 или
или 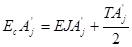 . (3.5)
. (3.5)
ПРИМЕР. Пусть заданы следующие значения звеньев размерной цепи, приведенной на рис. 6: увеличивающее А2=49,2 мм и уменьшающие А1’=1,1-0,25 мм; A3’=17-0,12 мм; А4'=14 мм; A5’=17-0,120 мм; Следует определить допуск и отклонение замыкающего звена АD.
По формуле (3.1) находим номинальный размер замыкающего звена:
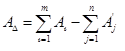 ,
,
АD = 49,2 - (1,1 + 17 + 14 + 17) = 0,1 мм.
Рассчитываем значение Ес 168 по формуле (3.4):
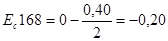 мм.
мм.
По формуле (3.5) определяем значение координат середин полей допусков уменьшающих звеньев:
 мм;
мм; 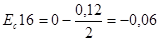 мм;
мм; 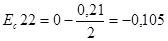 мм;
мм;
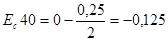 мм;
мм; 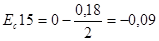 мм;
мм; 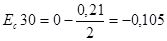 мм;
мм;
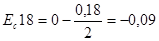 мм;
мм; 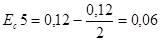 мм.
мм.
По формуле (3.3) подсчитываем значение ЕсАD:
ЕсАD=–0,20–(0.06–0,06–0,105–0,125–0,09–0,105–0,009–0,06–0,06)= =0,32 мм.
Рассчитаем допуск замыкающего звена по формуле (3.2):
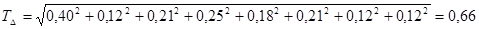 мм.
мм.
Предельные отклонения замыкающего звена рассчитываются по формулам:

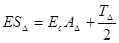 ;
;
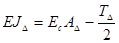 (3.6)
(3.6)
Следовательно:  мм;
мм;
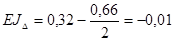 мм.
мм.
Окончательно имеем следующее замыкающее звено: 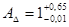 мм.
мм.
3.3 Решение второй задачи
Вторая задача распространена в практике машиностроения в значительно бо<