Линейная и векторная алгебра
для специальностей:
110301.65 - механизация сельского хозяйства.
110304.65 - технология обслуживания и ремонта машин в АПК.
050501.65 - профессиональное обучение.
Волгоград 2008
Линейная и векторная алгебра. Методическое пособие.
/Сост. А.А. Шубович, д.т.н. Ю.В. Клочков. Волгогр. Гос. с.-х. акад. Волгоград, 2008. 16 с.
При изучении математики перед студентами встаёт много вопросов и проблем. К таковым относится большое количество теоретического материала и формул, запоминание которых представляет определённые трудности. К тому же, как показывает практика, большинство студентов пренебрегают возможностью посещать библиотеки и не приносят на практические занятия рекомендуемые им учебники и сборники задач, несмотря на то, что таковые есть в наличии. Всё это отрицательно сказывается на качестве знаний. Помочь в решении данных проблем могут разработанные преподавателями методические указания по текущему разделу. При этом излагаются основные теоретические сведения, приводятся образцы решения типичных задач. Даются задания для текущего и итогового контроля знаний.
Практические занятия.
Первый семестр. I модуль. 10 занятий. (с 1.09 по 15.10)
Раздел 1.1: «Линейная алгебра».
1-е занятие. Матрицы и действия с ними. Обратная матрица.
Повторить: понятие матрицы, свойства матрицы; определителя матрицы второго и третьего порядка; обратной матрицы и способа её вычисления.
Опр. Матрицей размера n  m называется упорядоченная совокупность nm чисел, расположенных в виде таблицы из n строк и m столбцов:
m называется упорядоченная совокупность nm чисел, расположенных в виде таблицы из n строк и m столбцов:
 ,
,  ,
, 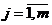 ,
,
где  - номер строки,
- номер строки,  - номер столбца.
- номер столбца.
Если в матрице число строк равно числу столбцов (n=m), то матрица называется квадратной n -го порядка, а в противном случае – прямоугольной.
Пример. 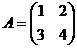 - квадратная матрица 2×2 второго порядка;
- квадратная матрица 2×2 второго порядка;
Диагональ с элементами 1 и 4 называется главной, с элементами 2 и 3 – побочной.
Матрица называется диагональной, у которой все элементы, кроме главной диагонали, не равны нулю, и единичной называется диагональная, у которой все элементы на главной диагонали равны 1.
Пример.  - диагональная,
- диагональная,  - единичная матрица третьего порядка.
- единичная матрица третьего порядка.
Операции над матрицами.
1).Сложение матриц:  ,
,  ,
, 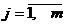 , или
, или 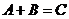 .
.
2). Опр. Произведением матрицы на число:  ,
,  ,
, 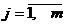 .
.
3). Опр. Произведением матрицы  размера
размера  и
и  размера
размера  называют матрицу С размера
называют матрицу С размера  , элементы
, элементы  которой вычисляются по формуле:
которой вычисляются по формуле:  . При этом число столбцов матрицы А должно быть равно числу строк матрицы В. В противном случае произведение не определено. При умножении используем запись:
. При этом число столбцов матрицы А должно быть равно числу строк матрицы В. В противном случае произведение не определено. При умножении используем запись: 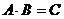 или
или  .
.
Опр. Матрица  , обратная к матрице
, обратная к матрице  определяется равенством:
определяется равенством: 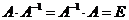 .
.
Способ нахождения  :
:
1). Составить матрицу 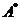 , заменяя в матрице
, заменяя в матрице  каждый элемент алгебраическим дополнением
каждый элемент алгебраическим дополнением  .
.
2). Составить 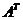 для
для 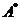 (поменять местами строки и столбцы относительно главной диагонали).
(поменять местами строки и столбцы относительно главной диагонали).
3). 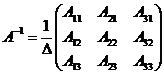 , где
, где  - определитель матрицы
- определитель матрицы  .
.
Задания для решения.
1. Найти сумму матриц  и
и 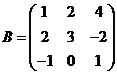 .
.
Ответ:  .
.
2. Найти матрицу  , если
, если  ,
,  .
.
Ответ:  .
.
3. Найти произведения матриц  и
и 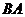 , если
, если  и
и  .
.
Ответ:  ;
;  .
.
4. Найти произведение матриц:
а). 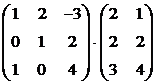 ; б).
; б). 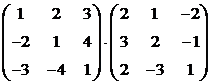 .
.
Ответ: а).  ; б).
; б).  .
.
5. Найти 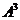 , если
, если  .
.
Ответ:  .
.
6. Найти значение матричного многочлена  при
при  , если
, если 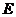 - единичная матрица третьего порядка.
- единичная матрица третьего порядка.
Ответ:  .
.
7. Найти  и сделать проверку.
и сделать проверку.
а).  ; б).
; б). 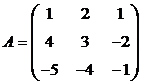 .
.
Ответ: а).  ; б).
; б).  .
.
2-е занятие. Вычисление определителей.
Повторить: формулу для вычисления определителей второго и третьего порядка, свойства определителей, правила решений системы уравнений по правилу Крамера и с помощью обратной матрицы.
Площадь треугольника с вершинами  ,
, 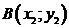 ,
,  :
:
 , где знак выбирается таким образом, чтобы площадь была положительной.
, где знак выбирается таким образом, чтобы площадь была положительной.
Задания для решения.
1. Вычислить определители:
а).  . б).
. б).  . в).
. в). 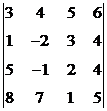 .
.
г).  . д).
. д). 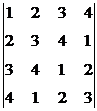 . е).
. е).  .
.
Ответ: а). 5; б). 80; в). 222; г). 396; д). 160; е). 148.
Решение. а). 
 .
.
2. Представить произведение определителей в виде определителя этого же порядка:
а).  . б).
. б).  .
.
Ответ: а).  . б).
. б).  .
.
3. Вычислить определитель 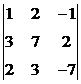 , разложив его по элементам третьей строки. Ответ: 0.
, разложив его по элементам третьей строки. Ответ: 0.
4. Вычислить определитель:  .
.
5. Решить систему уравнений по правилу Крамера и с помощью обратной матрицы:
а).  б).
б). 
Ответ: а).  . б).
. б).  .
.
Решение. а). I способ. Вычислим определители:  ,
, 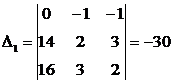 ,
,  ,
,  . По формулам Крамера
. По формулам Крамера  ,
,  ,
,  .
.
II способ. Систему уравнений запишем в матричном виде  , откуда
, откуда  . Вычислим алгебраические дополнения матрицы
. Вычислим алгебраические дополнения матрицы 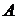 :
: 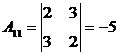 ,
,  ,
,  ,
,
 ,
,  ,
, 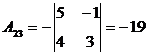 ,
,  ,
, 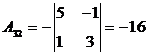 ,
,  . Тогда обратная матрица
. Тогда обратная матрица 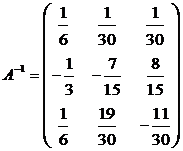 . Решение системы уравнений:
. Решение системы уравнений: 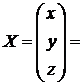
 .
.
6. Лежат ли на одной прямой точки:  ?
?
Указание. Применить формулу площади треугольника.
3-е занятие. Вычисление ранга матрицы и обратной матрицы с помощью элементарных преобразований.
Повторить: определение ранга матрицы, элементарные преобразования (ЭП) матрицы, способы нахождения ранга матрицы.
Опр. Рангом матрицы называется наибольший порядок минора этой матрицы, отличный от нуля. Ранг матрицы не изменяется от элементарных преобразований. Ранг матрицы  обозначается
обозначается  .
.
Пример 1. Найти ранг матрицы: а).

 , т.к.
, т.к.  .
.
б). 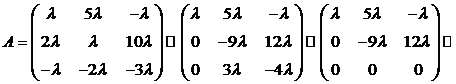
 ,
,  при
при 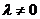 и
и  при
при  .
.
Пример 2. Вычислить  для матрицы
для матрицы 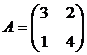 с помощью ЭП.
с помощью ЭП.
Решение. 


 . Проверка.
. Проверка.  ;
;  .
.
Задания для решения.
1. Найти ранг матрицы:
а).  . б).
. б).  . в).
. в).  .
.
г).  .д).
.д).  .
.
е).  .
.
Ответ: а). 3. б). 3. в). 2. г). 2. д). 1. е). 3.
2. Вычислить  для матриц с помощью ЭП.
для матриц с помощью ЭП.
а). 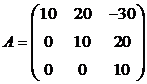 . б).
. б). 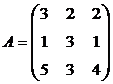 .
.
Ответ: а).  . б).
. б).  .
.
4-е занятие. Контрольная работа №1. по теме «Линейная алгебра».
Примерный вариант контрольной работы.
1. Вычислить определители: а).  . б).
. б).  .
.
2. Найти ранг матрицы:  .
.
3. Для матрицы 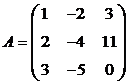 найти обратную ей.
найти обратную ей.
4. Доказать совместность системы уравнений  и решить её двумя способами: по формулам Крамера и методом обратной матрицы.
и решить её двумя способами: по формулам Крамера и методом обратной матрицы.