Алгоритм Диффи-Хеллмана
Алгори́тм Ди́ффи - Хе́ллмана — алгоритм, позволяющий двум сторонам получить общий секретный ключ, используя незащищенный от прослушивания, но защищённый от подмены, канал связи. Этот ключ может быть использован для шифрования дальнейшего обмена с помощью алгоритма симметричного шифрования.
Алгоритм был впервые опубликован Уитфилдом Диффи (Whitfield Diffie) и Мартином Хеллманом в 1976 году.
В 2002 году Хеллман предложил называть данный алгоритм «Диффи — Хеллмана — Меркля », признавая вклад Меркля в изобретение криптографии с открытым ключом.
Описание алгоритма
Предположим, что обоим абонентам известны некоторые два числа g и p (например, они могут быть «зашиты» в программное обеспечение), которые не являются секретными и могут быть известны также другим заинтересованным лицам. Для того, чтобы создать неизвестный более никому секретный ключ, оба абонента генерируют большие случайные числа: первый абонент — число a, второй абонент — число b. Затем первый абонент вычисляет значение  и пересылает его второму, а второй вычисляет
и пересылает его второму, а второй вычисляет  и передаёт первому. Предполагается, что злоумышленник может получить оба этих значения, но не модифицировать их (то есть у него нет возможности вмешаться в процесс передачи). На втором этапе, первый абонент на основе имеющегося у него a и полученного по сети B вычисляет значение
и передаёт первому. Предполагается, что злоумышленник может получить оба этих значения, но не модифицировать их (то есть у него нет возможности вмешаться в процесс передачи). На втором этапе, первый абонент на основе имеющегося у него a и полученного по сети B вычисляет значение  , а второй абонент на основе имеющегося у него b и полученного по сети A вычисляет значение
, а второй абонент на основе имеющегося у него b и полученного по сети A вычисляет значение  . Как нетрудно видеть, у обоих абонентов получилось одно и то же число:
. Как нетрудно видеть, у обоих абонентов получилось одно и то же число:  . Его они и могут использовать в качестве секретного ключа, поскольку здесь злоумышленник встретится с практически неразрешимой (за разумное время) проблемой вычисления
. Его они и могут использовать в качестве секретного ключа, поскольку здесь злоумышленник встретится с практически неразрешимой (за разумное время) проблемой вычисления  по перехваченным
по перехваченным  и
и  , если числа p, a, b выбраны достаточно большими.
, если числа p, a, b выбраны достаточно большими.


Алгоритм Диффи — Хеллмана,
где K — итоговый общий секретный ключ
При работе алгоритма, каждая сторона:
1. генерирует случайное натуральное число a — закрытый ключ
2. совместно с удалённой стороной устанавливает открытые параметры p и g (обычно значения p и g генерируются на одной стороне и передаются другой), где
p является случайным простым числом
g является первообразным корнем по модулю p
3. вычисляет открытый ключ A, используя преобразование над закрытым ключом

4. обменивается открытыми ключами с удалённой стороной
5. вычисляет общий секретный ключ K, используя открытый ключ удаленной стороны B и свой закрытый ключ a
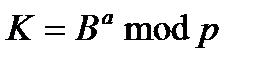
К получается равным с обеих сторон, потому что:

В практических реализациях, для a и b используются числа порядка 10100 и p порядка 10300. Число g не обязано быть большим и обычно имеет значение в пределах первого десятка.
Пример
Рома - криптоаналитик. Она читает пересылку Боба и Алисы, но не изменяет содержимого их сообщений.
- s = секретный ключ. s = 2
- g = открытое простое число. g = 5
- p = открытое простое число. p = 23
- a = секретный ключ Алисы. a = 6
- A = открытый ключ Алисы. A = gamod p = 8
- b = секретный ключ Боба. b = 15
- B = открытый ключ Боба. B = gbmod p = 19
| Алиса | Боб | Ева | |||
| Знает | Не знает | Знает | Не знает | Знает | Не знает |
p=23 g=5 a=6  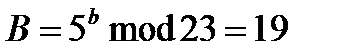    s=2 s=2
| b=? | p=23 g=5 b=15   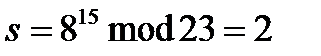   s=2 s=2
| a=? | p=23 g=5     
| a=? b=? s=? |
Шифрование с открытым ключом
Данный алгоритм может также использоваться в качестве алгоритма шифрования с открытым ключом. В этом случае общая схема остаётся аналогичной приведённой выше, но с небольшими отличиями. Алиса не передаёт значения p, g и A Бобу напрямую, а публикует их заранее в качестве своего открытого ключа. Боб выполняет свою часть вычислений, после чего шифрует сообщение симметричным алгоритмом, используя K в качестве ключа, и передаёт шифротекст Алисе вместе со значением B. Однако такой подход не получил распространения, в этой области доминирует алгоритм RSA.