В модели полиномиальных лагов предполагается, что зависимость коэффициентов при лаговых значениях объясняющей переменной от величины лага описывается полиномом m -ой степени. Модель имеет вид:
yt = a + b 0 xt + b 1 xt –1 + … + bp xt – p + et,
где
bs = g 0 + g 1 S + g 2 S 2 +… + gm Sm, 
Предположим, что величина лага p известна. Кроме того, необходимо установить степень полинома m. Обычно на практике ограничиваются рассмотрением полиномов 2-ой и 3-ей степени.
Пусть, например, p = 3, m = 2, тогда исходная модель есть:
yt = a + b 0 xt + b 1 xt –1 + b 2 xt –2 + b 3 xt –3 + et,
где
b 0 = g 0,
b 1 = g 0 + g 1 + g 2,
b 2 = g 0 + 2 g 1 + 4 g 2,
b 3 = g 0 + 3 g 1 + 9 g 2.
Преобразованная модель имеет вид:
yt = a + g0z0 + g1z1 + g2z2,
где
z 0 = xt + xt– 1 + xt– 2 + xt– 3,
z 1 = xt– 1 + 2 xt– 2 + 3 xt– 3,
z 2 = xt– 1 + 4 xt– 2 + 9 xt– 3.
Используя МНК, оцениваем параметры преобразованной модели и затем рассчитываем параметры исходной модели с распределенным лагом.
Пример 2.1. Имеются данные об объеме валового внутреннего продукта y некоторой страны в зависимости от инвестиций x в ее экономику за 25 лет.
Построим модель с распределенным лагом для p = 3 в предположении, что структура лага описывается полиномом второй степени.
Общий вид исходной модели есть:
yt = a + b 0 xt + b 1 xt- 1 + b 2 xt- 2 + b 3 xt -3 + et
Исходные (yt, xt) и преобразованные (z 0, z 1, z 2) данные (усл. ед) представлены в следующей таблице:
| 
| 
| 
| 
| 
|
| ---- | ---- | ---- | |||
| ---- | ---- | ---- | |||
| ---- | ---- | ---- | |||
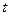
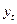
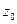
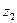
Оцененная исходная модель имеет вид
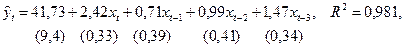
в которой коэффициент 0,71 при переменной xt –1 незначим (в скобках указаны стандартные ошибки).
Оцененная преобразованная модель имеет вид:
,
и все коэффициенты при переменных значимы.
Получили следующие оценки параметров преобразованной модели:
g 0 = 2,32, g 1 = –1,92, g 2 = 0,56.
Коэффициенты регрессии исходной модели:
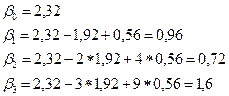
Таким образом, модель с распределенным лагом имеет вид:
.
Краткосрочный мультипликатор равен 2,32, а долгосрочный мультипликатор равен 2,32 + 0,96 + 0,72 + 1,6 = 5,6. Это означает, что увеличение инвестиций в экономику страны на 1 усл. ед приведет к росту валового внутреннего продукта в среднем на 2,32 усл. ед. в текущем периоде, и на 5,6 усл. ед. через 3 года.
Модели авторегрессии
Пусть имеется модель авторегрессии вида
.
Для интерпретации коэффициентов модели авторегрессии сделаем предположение о наличии бесконечного лага в воздействии текущего значения зависимой переменной на её последующие значения и о выполнении неравенства | b 1| < 1 (условие устойчивости).
В краткосрочном (текущем) периоде влияние x на y отражается величиной 
(краткосрочный мультипликатор). Он характеризует краткосрочное изменение y под влиянием изменения x на единицу своего измерения.
В долгосрочной перспективе суммарное влияние x на y отражается величиной 
(долгосрочный мультипликатор):
В модели авторегрессии объясняющая переменная yt– 1 находится непосредственно под воздействием et –1 и косвенно – под влиянием всех предшествующих значений случайного члена. Следовательно, объясняющая переменная yt –1 и случайный член et зависимы, и МНК не дает несмещенных оценок.
В этом случае одним из возможных методов оценки параметров уравнения авторегрессии является метод инструментальных переменных.
В качестве инструментальной переменной можно взять переменную
xt– 1, которая коррелирована с yt– 1 и некоррелирована с et. Практически, в качестве инструментальной переменной можно взять оценку
,
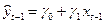полученную из предполагаемой линейной зависимости yt -1 от xt– 1.
Тогда оценку параметров модели авторегрессии можно найти обычным МНК из соотношения:
,
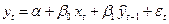где xt , yt – исходные, а 
– расчетные данные.
Практическая реализация метода инструментальных переменных осложняется появлением мультиколлинеарности факторов xt и в модели.
Пример 2.2. Построим модель авторегрессии по данным о среднедушевом располагаемом доходе x и среднедушевых расходах на конечное потребление y за 32 года.
Исходные и расчетные данные (усл. ед.) представлены в следующей таблице.
| 
|
|
| 
|
| 65,58 | 0,57 | |||
| 66,5 | 0,85 | |||
| 68,34 | 1,79 | |||
| 69,26 | 1,47 | |||
| 72,94 | 0,76 | |||
| 76,62 | 0,85 | |||
| 79,38 | 0,078 | |||
| 82,15 | 0,3 | |||
| 84,91 | 0,31 | |||
| 86,75 | -1,34 | |||
| 89,51 | -1,32 | |||
| 91,35 | 0,03 | |||
| 94,11 | -2,14 | |||
| 99,63 | -2,32 | |||
| 97,79 | -1,06 | |||
| 97,79 | -0,25 | |||
| 101,47 | 0,63 | |||
| 103,31 | 0,18 | |||
| 106,99 | -0,93 | |||
| 108,84 | -2,19 | |||
| 108,84 | -1,98 | |||
| 109,76 | -2,11 | |||
| 109,76 | 0,29 | |||
| 111,6 | -1,54 | |||
| 118,04 | -0,84 | |||
| 120,8 | 0,17 | |||
| 122,64 | 2,11 | |||
| 123,56 | 2,59 | |||
| 126,32 | 2,40 | |||
| 127,24 | 1,48 | |||
| 128,16 | 1,14 |
Определим по этим данным параметры модели авторегрессии вида
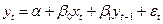
Применение обычного МНК для оценки параметров этой модели приводит к результатам:
(в скобках указаны стандартные ошибки).
Однако, как было отмечено выше, оценка параметра b 1 = 0,455 является смещенной. Для получения несмещенных оценок параметров этого уравнения воспользуемся методом инструментальных переменных.
Оценка уравнения регрессии 
обычным МНК дает:
(в скобках указаны стандартные ошибки).
Тогда оценка модели авторегрессии 
обычным МНК дает следующие результаты:
(в скобках указаны стандартные ошибки).
Применение метода инструментальных переменных привело к статистической незначимости оценки b 1 = 0,141 при переменной . Это произошло ввиду высокой мультиколлинеарности переменных xt и .
Поскольку ни один из методов оценок параметров модели авторегрессии не привел к достоверным результатам, следует использовать другие методы оценок.
Заметим, что для данной модели авторегрессии при наличии автокорреляции остатков не существует состоятельного метода оценивания.
В качестве примера произведем проверку гипотезы о наличие автокорреляции в модели регрессии, полученной методом инструментальных переменных. Проверку произведем по критерию h- Дарбина.
Коэффициент автокорреляции остатков первого порядка r = 0,722, следовательно, значение DW = 0,556.
Значение h- критерия Дарбина определяется выражением
,
что указывает на положительную автокорреляцию остатков.
2.3. Примеры моделей с лагированными переменными.
Модель частичной корректировки
В модели частичной корректировки предполагается, что поведенческое уравнение определяет не фактическое значение зависимой переменной yt, а её желаемый (целевой) уровень:
yt * = a + b xt + et, et ~ N (0; s 2) (2.1)
Предполагается также, что фактическое значение зависимой переменной не выходит мгновенно на желаемый уровень, а изменяется только на долю l в нужном направлении:
yt – yt –1 = l (yt* – yt- 1),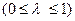 
(2.2)
Это выражение можно переписать следующим образом:
yt = l yt* + (1 – l) yt –1,
откуда видно, что yt получается как взвешенное среднее желаемого уровня и фактического значения этой переменной в предыдущем периоде.
Параметр l называется корректирующим коэффициентом. Чем больше l, тем быстрее происходит процесс корректировки. Если значении l = 1, то yt = yt* и полная корректировка происходит за один период. Если l = 0, то корректировка yt не происходит совсем.
Подставляя yt* в выражение для yt, получим
yt = a l + b l xt + (1 – l) yt- 1 + l et. (2.3)
Полученное уравнение включает только фактические значения переменных.
Поскольку случайные члены некоррелированы, состоятельные оценки параметров можно получить, применяя МНК к оцениванию составных параметров 
в уравнении (2.3).
Пример 2.3. Производственные компании распределяют прибыль П, оставшуюся после уплаты налогов: одну часть на выплату доходов акционерам в форме дивидендов (D), другую – на финансирование инвестиций.
Известны данные (усл. ед.) о деятельности производственных компаний за ряд предыдущих лет.
| t | D | П | t | D | П |
Предположим, что у фирмы имеется целевая долгосрочная доля выплат g и что желаемый объем дивидендов Dt* соотносится с текущей прибылью Пt как Dt* = g Пt + et. Однако реальный объем дивидендов подвержен процессу частичной корректировки:
Dt – Dt –1 = l (Dt* – Dt –1),
или
Dt = g l Пt + (1 – l) Dt –1 + l e t. (0 £ l £ 1).
На основе данных о деятельности производственных компаний за ряд лет построено уравнение регрессии
Dt = 68 + 0,29 Пt + 0,58 Dt– 1,
где все коэффициенты значимы.
Из соотношения 1 – l = 0,58 определяется корректирующий коэффициент l = 0,42, а из соотношения g l = 0,29 – оценка доли выплат g = 0,69.