ВВЕДЕНИЕ
Расчетно-графическая работа (РГР) по дисциплине «Информационные технологии в топливно-энергетическом комплексе» предназначена для выполнения студентами 1 курса, обучающимися по направлению 09.03.03 «Прикладная информатика» и профилю подготовки «Прикладная информатика в топливно-энергетическом комплексе».
Целью РГР является приобретение практических навыков обработки экспериментальных данных с использованием прикладных программных продуктов, необходимых в будущей профессиональной деятельности.
В РГР студент должен показать:
1) знание методики построения математической модели по методу Брандона;
2) умение использовать прикладные программные продукты для построения статистической модели множественной нелинейной регрессии;
3) умение делать выводы;
4) навыки владения современной вычислительной техникой.
Цель работы: получение основных навыков обработки экспериментальных данных в программе электронных таблиц Excel.
Задачи работы:
- построение математической модели по методу Брандона;
- ранжирование влияющих факторов;
- выбор вида зависимости и построение статистической модели.
ПРАКТИЧЕСКАЯ ЧАСТЬ
Для составления данной математической модели необходимы исходные данные, которые приведены в таблице 1.
Таблица 1 – Исходные данные для построения уравнения множественной нелинейной регрессии
| x1 | x2 | x3 | yи |
| 0,2722372 | |||
| 0,2429079 | |||
| 0,4336491 | |||
| 0,7375712 | |||
| 0,3290287 | |||
| 0,6054599 | |||
| 0,3478156 | |||
| 0,7228922 | |||
| 0,4508846 | |||
| 0,3700496 | |||
| 0,562687 | |||
| 0,7271149 | |||
| 0,4174476 | |||
| 0,5690065 | |||
| 0,4560555 | |||
| 0,4145176 | |||
| 0,4429564 | |||
| 0,4420946 | |||
| 0,6713288 | |||
| 0,358376 | |||
| 0,6288142 |
|
|
1. По заданию необходимо составить математическую модель определённого процесса по методу Брандона. По этому методу уравнение регрессии имеет вид:  .
.
При использовании метода Брандона важен порядок следования функций в уравнении. Чем большее влияние оказывает независимый фактор на зависимый, тем меньшим должен быть его порядковый номер в указанном уравнении. Поэтому задача построения модели нелинейной множественной регрессии по методу Брандона разбивается на несколько этапов: ранжирование влияющих факторов; выбор вида зависимости и построение статистической модели.
2. Построение поля корреляции для исходных данных - yиj – хkj (j – количество экспериментальных точек) (Рисунок 1).

Рисунок 1 – поле корреляции для исходных данных
3. Расчёт определителей матриц, полученных путём вычеркивания из корреляционной матрицы соответствующего столбца и строки. Данные определители (Dij) в дальнейшем применяются для расчёта коэффициентов множественной корреляции (Рисунок 2).

Рисунок 2 – Определители из корреляционной матрицы
4. Расчет коэффициентов множественной корреляции по формуле (Рисунок 3):
 ,
,
где r– коэффициент множественной корреляции, Dn+1,k,Dkk– определители.
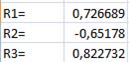
Рисунок 3 – Коэффициенты множественной корреляции
5. Оценка степени влияния k-го независимого фактора на зависимый фактор y и определение порядка следования функции в уравнении:
|
|
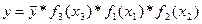
Как видно из данной формулы, наибольшее влияние оказывает независимая переменная x3, а наименьшее – x2.
6. Представление исходных значений зависимого фактора в каждом наблюдении в безразмерной форме (Рисунок 4).

Рисунок 4 – Исходные значения зависимого фактора
7. Поиск первой зависимости, для чего будут использованы нормированные значения вектора зависимых факторов (y0) и исходные значения первого влияющего фактора (x3) (Рисунок 5).
В качестве линии тренда был выбран полином второй степени, так как при этом коэффициент детерминации (R2) наиболее близок к значению «1».

Рисунок 5 – График зависимости у0 и исходные значения x3
8. Расчет значений первой зависимости и определение остаточного показателя  для каждого исходного значения зависимого фактора (Рисунок 6).
для каждого исходного значения зависимого фактора (Рисунок 6).

Рисунок 6 – Расчёт переменной у1 и уи1
9. Поиск второй зависимости, для чего будут использованы значения вектора остаточных показателей(yи1) и исходные значения второго влияющего фактора (x1) (Рисунок 7).

Рисунок 7 – График зависимости yи1 и x1
10. Проводя аналогичные расчёты находим значения для у2 и у3
(Рисунок 8). В ходе этих вычислений получаем полноценную модель множественной нелинейно регрессии, которая имеет вид:
y = 0,2722372 * (0,0705x2 - 0,3425x + 1,0931)*(5*10-6x3 - 0,0049x2 + 1,4481x - 142,7)*(6*10-6x3 - 0,0003x2 + 0,0051x - 0,0122);

Рисунок 8 - Расчёт переменной у2 и уи2,у3, относительной погрешности и урасч
11. Поиск третьей зависимости, для чего будут использованы значения вектора остаточных показателей(yи2) и исходные значения второго влияющего фактора (x2) (Рисунок 9).
|
|

Рисунок 9 - График зависимости yи2 и x2
Чтобы получить полноценную картину о правильности построения данной математической модели, построенной по методу Брандона, необходимо построить график зависимости между исходными значениями yи и урасч (Рисунок 10).

Рисунок 10 – График зависимости между уи и урасч
Как видно из рисунка 8 и 10, метод Брандона не подходит для данной математической модели, так как погрешность в каждой экспериментальной точке очень высока, а зависимость между расчётными и исходными значениями незначительна (коэффициент детерминации R2=0,45). Для построения адекватной математической модели нужно использовать другой метод, либо провести повторный эксперимент и дать более точные исходные значения.
ЗАКЛЮЧЕНИЕ
СПИСОК ИСПОЛЬЗОВАНЫХ ИСТОЧНИКОВ
1. Галеев Э. Р., Елизаров В. В., Елизаров В. И. Моделирование систем: программа, контрольные задания, методические указания для студентов заочной формы обучения: Нижнекамск: Изд-во Нижнекамский химико-технический институт (филиал) КГТУ, 2009.
2. Многофакторная зависимость. Метод Брандона [Электронный ресурс] // Математическое моделирование.
URL: https://media.ls.urfu.ru/589/1606/3818/5224/ (дата обращения: 16.05.2018)