Решение.

Пример.
Найти угол  между векторами
между векторами  ,
,  .
.
Решение.
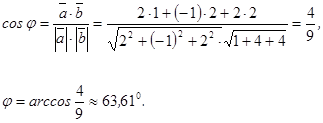
Векторное произведение геометрических векторов
Векторным произведением двух векторов  и
и 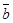 , называется вектор
, называется вектор 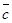 =
=  ×
× 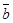 , удовлетворяющий трем условиям:
, удовлетворяющий трем условиям:
1. | 
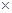
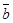 | =
| =  ∙
∙  ∙sinφ, где φ – угол между векторами
∙sinφ, где φ – угол между векторами  и
и 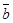 в промежутке [0;1800];
в промежутке [0;1800];
2. 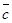

 ,
, 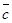

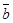 ;
;
3. если смотреть с конца вектора 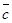 на плоскость, в которой лежат векторы
на плоскость, в которой лежат векторы  и
и 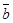 , то кратчайший поворот от вектора
, то кратчайший поворот от вектора  до
до 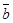 будет виден совершающимся против часовой стрелки (правило правого винта).
будет виден совершающимся против часовой стрелки (правило правого винта).
Применяется векторное произведение для вычисления площадей многоугольников. С помощью векторного произведения можно установить признак параллельности векторов, а именно, два вектора тогда и только тогда взаимно параллельны, когда их векторное произведение равно нулевому вектору. Отметим, что в этом случае удобнее пользоваться признаком: два вектора взаимно параллельны тогда и только тогда, когда их координаты пропорциональны. Оно имеет и другие применения, но в основном в физико-технических задачах.
Из первого пункта определения векторного произведения следуют формулы:
│ 
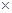
 │ = S – площадь параллелограмма ABCD;
│ = S – площадь параллелограмма ABCD;
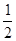 │
│ 
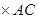 │ = S – площадь треугольника ABC.
│ = S – площадь треугольника ABC.
Векторное произведение обладает свойствами:
1) 
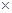
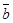 = – (
= – (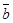
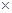
 ); 2)
); 2) 
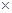 (
(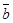 +
+  ) = (
) = (
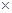
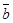 ) + (
) + (
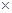
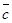 );
);
3) m 
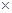 n
n 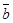 = (m n) (
= (m n) (
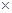
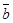 ), где m,n
), где m,n  R.
R.
Применяется векторное произведение для вычисления площадей многоугольников. С помощью векторного произведения можно установить признак параллельности векторов, а именно, два вектора тогда и только тогда взаимно параллельны, когда их векторное произведение равно нулевому вектору. Отметим, что в этом случае удобнее пользоваться признаком: два вектора взаимно параллельны тогда и только тогда, когда их координаты пропорциональны. Оно имеет и другие применения, но в основном в физико-технических задачах.
Из первого пункта определения векторного произведения следуют формулы:
│ 
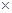
 │ = S – площадь параллелограмма ABCD;
│ = S – площадь параллелограмма ABCD;
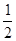 │
│ 
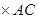 │ = S – площадь треугольника ABC.
│ = S – площадь треугольника ABC.
Векторное произведение обладает свойствами:
1) 
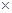
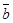 = – (
= – (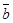
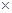
 ); 2)
); 2) 
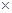 (
(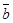 +
+  ) = (
) = (
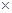
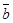 ) + (
) + (
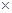
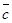 );
);
3) m 
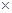 n
n 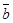 = (m n) (
= (m n) (
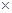
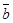 ), где m, n
), где m, n  R.
R.
Пользуясь свойствами векторного произведения и его определением, можно получить формулу:

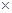
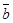 =
=  ,
,
где  =
=  .
.
Пример. Вычислить площадь треугольника с вершинами А(1,1,2), В(0;2;4),С(-1;3;0).
Решение.  =(0-1; 2-1; 4-2)= (-1; 1; 2),
=(0-1; 2-1; 4-2)= (-1; 1; 2),  = (-1-1; 3-1; 0-2)= =(-2;2;-2).
= (-1-1; 3-1; 0-2)= =(-2;2;-2).
 │
│ 
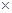
 │=
│=  │
│ 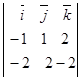

Пример. Вычислить площадь треугольника с вершинами
 .
.
Решение. Будем считать, что третья координата вершин треугольника равна нулю. Тогда:
 =(
=( ;
;  ;0),
;0),  = (
= ( ;
; 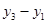 ; 0).
; 0).
│ 
 │=
│=
│  │.
│.
Получили формулу площади параллелограмма со смежными сторонами 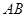 и
и  . Формула площади треугольника АВС имеет вид:
. Формула площади треугольника АВС имеет вид:
 │
│  │.
│.
Смешанное произведение
Определение. Смешанным произведением трех векторов 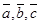 называется число
называется число  .
.
Применяя свойства векторного и скалярного произведения, можно получить формулу:
 =
= 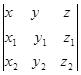 ,
,
где  .
.
Так как
 =
= 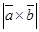
 ,
,
где величина 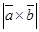 равна площади параллелограмма, построенного на векторах – сторонах
равна площади параллелограмма, построенного на векторах – сторонах  , а величина
, а величина  равна высоте параллелепипеда, построенного на векторах – сторонах
равна высоте параллелепипеда, построенного на векторах – сторонах 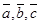 , то объем параллелепипеда вычисляется по формуле V =
, то объем параллелепипеда вычисляется по формуле V =  .
.
Пример. Вычислить объем пирамиды АBСD по ее вершинам А(1;1;0), В(0;2;4), С(-1;3;2), D(4;0;2).
Решение. Сначала находим векторы  .
.
 =(0-1;2-1;4-0)=(-1;1;4),
=(0-1;2-1;4-0)=(-1;1;4),  =(-1-1;3-1;2-0)=(-2;2;2),
=(-1-1;3-1;2-0)=(-2;2;2),
 =(4-1;0-1;2-0)=(3;-1;2).
=(4-1;0-1;2-0)=(3;-1;2).
Затем находим смешанное произведение векторов.

Потом находим объем параллелепипеда, построенного на векторах – сторонах  .
.
V = 
Так как объем пирамиды равен шестой части объема параллелепипеда, то ее объем равен 2.
Линейное преобразование векторного пространства
И его свойства
Определение. Преобразование векторного пространства называется линейным, если оно задается квадратной матрицей преобразования. Оно записывается в виде уравнения АХ = Х  , при этом Х
, при этом Х  называется образом вектора Х.
называется образом вектора Х.
Пример.
Найти образ вектора Х =  в линейном преобразовании, заданном матрицей А =
в линейном преобразовании, заданном матрицей А =  .
.
Решение.

 =
= 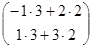 =
=  .
.
В этом примере вектор Х преобразовался в вектор, который имеет другую длину и другое направление.
Определение. Если выполняется равенство АХ =  Х, где Х
Х, где Х  О,
О,  , то Х называется собственным вектором, а
, то Х называется собственным вектором, а  называется собственным числом матрицы А.
называется собственным числом матрицы А.
Для нахождения собственных векторов матрицы А надо перейти от матричного уравнения АХ =  Х к однородной системе уравнений, из которой сначала найти
Х к однородной системе уравнений, из которой сначала найти  , а затем собственные векторы.
, а затем собственные векторы.
Пример. Найти собственные векторы матрицы

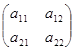 .
.
Решение.
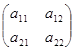
 =
=  ,
,  ,
,


Получили однородную систему уравнений.Нас интересует только не нулевое решение, а оно существует только тогда, когда определитель системы равен нулю. Решая уравнение
 = 0,
= 0,
которое называется характеристическим уравнением матрицы, находим собственные числа. А по собственным числам находим собственные векторы. Если преобразование задается матрицей

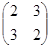 ,
,
тохарактеристическое уравнение имеет вид
 = 0.
= 0.
Его корни:  Если
Если  , то система равносильна уравнению 3 х
, то система равносильна уравнению 3 х  - 3 х
- 3 х  = 0 и тогда: х
= 0 и тогда: х  = х
= х  = t, t
= t, t  Если
Если  , то система равносильна уравнению 3 х
, то система равносильна уравнению 3 х  + 3 х
+ 3 х  = 0 и тогда: х
= 0 и тогда: х  = - х
= - х  = t,t
= t,t 
Ответ: t  , t
, t  – собственные векторы, t
– собственные векторы, t  .
.