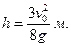1. Рассмотрим систему «лодка-человек». Поскольку в горизонтальном направлении на систему не действуют внешние силы, импульс ее вдоль горизонтальной оси Х сохраняется.. В начальный момент (человек и лодка покоятся) импульс системы равен 0. Значит, он будет равен 0 в любой последующий момент времени. Пусть скорость человека относительно Земли постоянна и равна V, а скорость лодки равна V1. Тогда в проекциях на ось Х 0 = mV – МV1. Пусть время движения человека вдоль лодки равно t. Тогда человек пройдет путь (V t), а лодка - путь (V1 t). В начальный момент человек и другой конец лодки находились на расстоянии L друг от друга, а затем начали двигаться навстречу друг другу со скоростями V и V1. Следовательно, L = V t + V1 t.
Решив совместно уравнения L = (V t + V1 t) и 0 = (mV – МV1 ), получим значение пути, пройденного лодкой (V1 t) = Х = m L / (М + m).
2, Используя принцип относительности движения V = V1 +V2, или V2 = V1 +V, где
V2 – скорость человека относительно лодки, V1 - скорость лодки, V - скорость человека относительно берега, получаем, что время перемещения человека вдоль лодки t = L / V2. За это время лодка проходит путь (V1t) = (V1L) / V2 или, с использованием закона сохранения импульса, (V1 t) = m L / (М + m).
РАЗДЕЛ 3. Динамика вращательного движения.
2. С наклонной плоскости, составляющей угол α = 300 с горизонтом, скатывается без скольжения шарик (рис.5.2). Пренебрегая трением, определить время движения шарика по наклонной плоскости, если известно, что его центр масс при скатывании понизился на h = 30 см.
| Дано: α = 300 h = 30 см = 0,3м _______________ t -? | 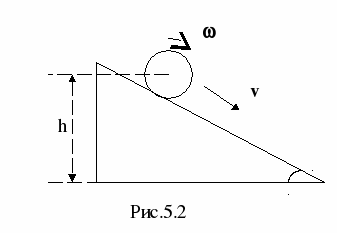
|
Решение:
Т.к. трения нет, воспользуемся законом сохранения механической энергии:
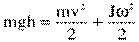 ,
,
где 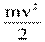 - кинетическая энергия поступательного движения шарика,
- кинетическая энергия поступательного движения шарика, 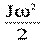 - кинетическая энергия вращательного движения шарика.
- кинетическая энергия вращательного движения шарика. 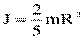 - момент инерции шарика относительно оси, проходящей через его центр,
- момент инерции шарика относительно оси, проходящей через его центр, 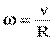 - угловая скорость вращения. Подставив все в закон сохранения энергии, найдем скорость поступательного движения шарика:
- угловая скорость вращения. Подставив все в закон сохранения энергии, найдем скорость поступательного движения шарика:
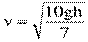 .
.
Поскольку движение шарика равноускоренное, воспользуемся следующими формулами:
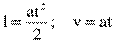 .
.
Выразим время:
 .
.
Воспользовавшись полученным ранее выражением для скорости, получим:
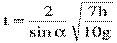 .
.
Подставив численные значения, имеем: t = 0,585 с.
Пример 4. К ободу однородного сплошного диска радиусом 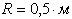 приложена постоянная касательная сила приложена постоянная касательная сила 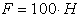 . При вращении диска на него действует момент . При вращении диска на него действует момент 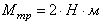 . Определите массу m диска, если известно, что его угловое ускорение ε постоянно и равно 16 рад/с2. . Определите массу m диска, если известно, что его угловое ускорение ε постоянно и равно 16 рад/с2.
| |||
| Дано | Решение | ||
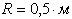
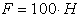
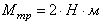
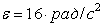
| 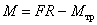 , ,
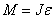 , ,
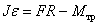 , ,
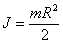 , ,
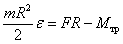 , ,
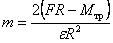 .
Ответ: .
Ответ: 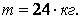
| ||
Пример 2. Вентилятор вращается с частотой 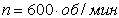 . После выключения он начал вращаться равнозамедленно и, сделав . После выключения он начал вращаться равнозамедленно и, сделав 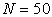 оборотов, остановился. Работа A сил торможения равна 31,4 Дж. Определите: 1) момент сил M торможения; 2) момент инерции J вентилятора. оборотов, остановился. Работа A сил торможения равна 31,4 Дж. Определите: 1) момент сил M торможения; 2) момент инерции J вентилятора.
| |||
| Дано | Решение | ||
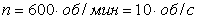
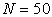
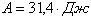
| 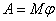 , ,
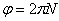 , ,
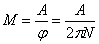 , ,
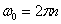 , ,
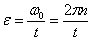 , ,
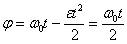 , ,
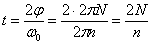 , ,
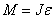 , ,
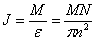 .
Ответ: 1) .
Ответ: 1) 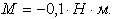 ;
2) ;
2) 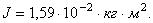
| ||
1) 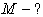 2)
2) 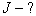
| |||
161. Платформа, имеющая форму сплошного однородного диска, может вращаться по инерции вокруг неподвижной вертикальной оси. На краю платформы стоит человек, масса которого в 3 раза меньше массы платформы. Определить, как и во сколько раз изменится угловая скорость вращения платформы, если человек перейдет ближе к центру на расстояние, равное половине радиуса платформы.

| РАЗДЕЛ 4!!! | |||||||||||
| |||||||||||
| Найти работу силы F = 30 Н, в результате действия которой груз массой m = 2 кг поднимается по наклонной плоскости на высоту h = 2,5 м с ускорением а =5 м/с2. Сила действует параллельно наклонной плоскости. Трением о плоскость пренебречь. | |||||||||||
Дано:
| Решение:
Второй закон Ньютона
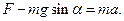 Найдем угол α
Найдем угол α
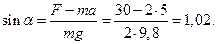 (Если принять
g = 10 м/с2, то sin α = 1, т.е. α = 90°, т.е. в условии
либо силу надо задавать меньше, либо ускорение принимать больше, либо массу взять больше, чтобы плоскость была наклонной)
Перемещение тела
(Если принять
g = 10 м/с2, то sin α = 1, т.е. α = 90°, т.е. в условии
либо силу надо задавать меньше, либо ускорение принимать больше, либо массу взять больше, чтобы плоскость была наклонной)
Перемещение тела
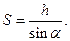 Работа силы
Работа силы
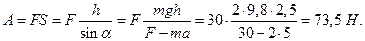 Ответ:
Ответ: 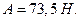
| ||||||||||
| Определить кинетическую энергию тела массой m =1,5 кг, брошенного горизонтально со скоростью v 0=20 м/с, в конце четвертой секунды его движения. Сопротивлением воздуха пренебречь. | |||||||||||
Дано:
| Решение:
Вертикальная составляющая скорости на высоте h
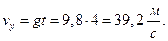 Скорость тела
Скорость тела
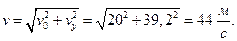 Кинетическая энергия тела
Кинетическая энергия тела
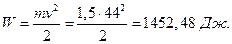 Ответ:
Ответ: 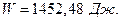
| ||||||||||
| Тело брошено вертикально вверх со скоростью v 0=49 м/с. На какой высоте его кинетическая энергия будет в 2 раза больше потенциальной? Сопротивлением воздуха пренебречь. | |||||||||||
Дано:
| Решение:
Энергия тела в момент бросания
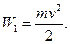 Полная энергия на высоте h
Полная энергия на высоте h
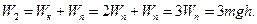 По закону сохранения энергии
По закону сохранения энергии
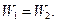
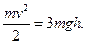 Искомая высота
Искомая высота
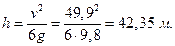 Ответ:
Ответ: 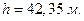
| ||||||||||


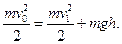 Искомая высота
Искомая высота
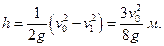 Ответ:
Ответ: