Цель работы: Изучение законов динамики вращательного движения. Экспериментальное определение момента инерции диска с помощью маятника Максвелла.
I. ВВЕДЕНИЕ
Маятник Максвелла – это устройство, состоящее из массивного диска, симметрично и жестко закрепленного на горизонтальной оси, подвешенной на двух нерастяжимых нитях. Выведенный из состояния равновесия маятник может совершать колебательные движения в вертикальной плоскости. Маятник состоит из легкой оси, на которой симметрично закреплен массивный диск. На концах оси закреплена нерастяжимая нить, проходящая через отверстия на верхней части штатива. В центре верхней части установки расположен регулировочный винт, с помощью которого можно регулировать положение оси в пространстве. В положении равновесия нити полностью размотаны, ось находится в горизонтальном положении. Для вывода маятника Максвелла из положения равновесия нити аккуратно наматываются на ось от концов к середине. Необходимо наматывать нити виток к витку для обеспечения равномерного разматывания и сохранения горизонтальности оси в процессе движения маятника. В верхнем положении маятник фиксируется с помощью электромагнитов. После отключения питания электромагнитов, под действием момента силы тяжести нити начинают разматываться, и маятник начинает движение. Движение маятника состоит из поступательного движения вниз и вращательного – вокруг оси симметрии. Под действием момента сил тяжести движения продолжается до полного разматывания нитей. После этого, очевидно, продолжение поступательного движения вниз невозможно, однако вращение продолжается по инерции. Это приводит к повторному наматыванию нитей на ось. В результате маятник вновь поднимается. По достижении высшей точки процесс повторяется. Периодичность этого процесса дает основания называть описанный прибор маятником.
Пусть теперь маятник имеет идеальную форму и лишен различных дефектов. Другими словами, два положения маятника, отличающиеся одно от другого только поворотом вокруг его продольной оси неотличимы друг от друга. Тогда, для описания движения маятника Максвелла необходимо и достаточно иметь в своем распоряжении всего одну координатную ось. Если в кинематике, вопрос о координатах материальной точки достаточно очевиден, то в динамике дело обстоит несколько сложнее. Для твердого тела удобно пользоваться точкой, в которой находится его центр масс. Это значит, что для маятника Максвелла применима теорема о движении центра масс.
В то же время, движение маятника Максвелла является примером плоского движения. Плоское движение твердого тела (движение, при котором все точки тела перемещаются параллельно некоторой неподвижной плоскости называется плоским) может быть представлено в виде движения некоторой неизменяемой двумерной фигуры в ее плоскости, при чем это движение должно являться суперпозицией поступательного движения какой-либо точки этой фигуры и вращения ее вокруг оси, проходящей через эту точку и перпендикулярной плоскости фигуры. Опять же, удобно использовать в качестве такой точки центр масс рассматриваемого тела.
Основываясь на сказанном можно выделить три основных этапа движения маятника, а именно: спуск, удар и подъем. В соответствии с этим, силы, действующие на маятник, должны быть подразделены на силы длительного действия (при спуске и подъеме) и силы кратковременного действия (удар). В первом случае эти силы не изменяются во времени, во втором – они резко нарастают и убывают. Отметим, что удар при опускании маятника отличается удара при столкновении двух тел. Во втором случае большая часть кинетической энергии переходит во внутреннюю энергию тел, в то время как при ударе маятника Максвелла кинетическая энергия его вращения полностью сохраняется неизменной. При этом энергия вращения гораздо больше, чем кинетическая энергия поступательного движения перед ударом.
Ознакомление с движением маятника Максвелла в задаче состоит в наблюдении его движения, которое, как уже было сказано, состоит из трех стадий: спуска, удара и подъема. Каждая из этих стадий рассматривается отдельно.
Перейдем теперь непосредственно к описанию движения маятника. Напомним, что для описания будет использоваться теорема о движении центра масс.
Уравнения движения маятника без учета сил трения имеют вид:
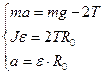 (1)
(1)
где m - масса маятника, J - момент инерции маятника, g - ускорение свободного падения. R 0 - радиус стержня, Т - сила натяжения одной нити, а - ускорение поступательного движения центра масс маятника, ɛ - угловое ускорение маятника. Решая систему уравнений (1) относительно ускорения и момента инерции маятника имеем:
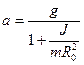 (2)
(2)
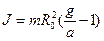 (3)
(3)
Поскольку момент инерции маятника можно представить в виде 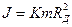 , где R Д - радиус диска и безразмерный коэффициент К ~ 1/2, величина
, где R Д - радиус диска и безразмерный коэффициент К ~ 1/2, величина 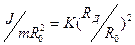 (радиус диска R Д много больше радиуса стержня R 0) и ускорение маятника а<<g, а сила натяжения нитей
(радиус диска R Д много больше радиуса стержня R 0) и ускорение маятника а<<g, а сила натяжения нитей
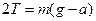 (4)
(4)
близка к весу маятника mg. Так как при равноускоренном движении (I стадия - опускание маятника)
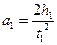 (5)
(5)
где t 1 - время опускания маятника, h 1 - расстояние, которое он проходит за это время, то для экспериментального определения момента инерции маятника из (3) и (5) получаем формулу:
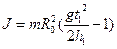 (6)
(6)
Для скорости опускания центра масс маятника непосредственно перед его ударом имеем
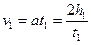 (7)
(7)
После удара при подъеме маятника вверх (III стадия) он движется равнозамедленно с ускорением а, направленным так же, как при его опускании вниз. Скорость движения центра масс маятника при подъеме определяется уравнением:
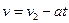
где v 2 - начальная скорость движения маятника вверх, t - время от начала этого движения. Появление этой скорости обусловлено продолжающимся по инерции вращением маятника в нижней точке его траектории. При этом вращении наматывание нитей на стержень маятника и приводит к его подъему.
Пусть время подъема маятника до его полной остановки в верхней точке равно t 2, тогда для величины начальной скорости имеем:
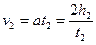 (8)
(8)
так как величина ускорения при подъеме маятника связана с расстоянием h 2, которое проходит его ось до остановки, таким же соотношением, как и при спуске:
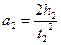 (9)
(9)
Момент инерции маятника J определяем по формуле:
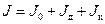 (10)
(10)
Момент инерции оси маятника J 0 определяем по формуле:
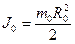 (11)
(11)
где R 0 -радиус оси; m 0 - масса оси;
Момент инерции диска маятника J д определяем по формуле:
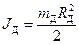 (12)
(12)
где R Д -радиус диска; m Д - масса диска.
Момент инерции кольца маятника J к определяем по формуле:
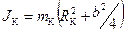 (13)
(13)
где R K - средний радиус кольца; m к - масса кольца, кг; b - ширина кольца, м.
II. ОПИСАНИЕ УСТАНОВКИ
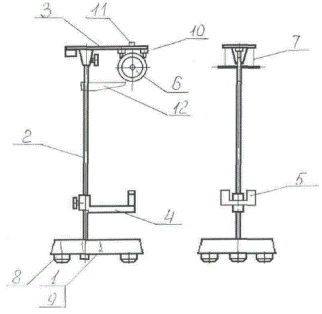
Установка представлена на рисунке и включает в свой состав: основание 1, вертикальную стойку 2, верхний кронштейн 3, кронштейн 4 для установки фотодатчика, фото датчик 5, диск 6 с осью, подвешенной на двух нитях 7, комплект из трех сменных колец с различными моментами инерции. Основание 1 снабжено тремя регулируемыми опорами 8 и зажимом 9 для фиксации вертикальной стойки 2. Вертикальная стойка 2 выполнена из металлической трубы, на которую нанесена миллиметровая шкала, и имеет визир 12. На верхнем кронштейне 3 размещаются электромагниты 10 и узел 11 регулировки исходного положения маятника. Кронштейн 4 имеет зажим для крепления на вертикальной стойке 2 и элементы фиксации фотодатчика.
III. ПРОВЕДЕНИЕ ЭКСПЕРИМЕНТА
Упражнение 1. Определение величин ускорений и скоростей маятника Максвелла при его спуске и подъеме.
1. Измерения
1. Определить высоту h1, с которой маятник опускается до удара, и время t1 спуска.
Для этого:
Установить нижний кронштейн с фотодатчиком в крайнее нижнее положение шкалы так, чтобы плоскость кронштейна, окрашенная в синий цвет, совпала с одной из рисок шкалы.
Произвести регулировку положения основания при помощи регулировочных опор так, чтобы диск на бифилярном подвесе находился в центре окна фотодатчика.
Установить с помощью узла регулировки необходимую длину бифилярного под-
веса таким образом, чтобы нижний край среза сменного кольца маятника находился на 4 - 5 мм ниже оптической оси фотодатчика; при этом ось маятника должна занимать горизонтальное положение.
Подключить фотодатчик и электромагниты установки к блоку при помощи кабеля. Вилку с маркировкой "Ф" вставить в розетку фотодатчика, а вилку с маркировкой "Э" в розетку электромагнитов.
Нажать кнопку "СЕТЬ". При этом должно включиться табло индикации и должны включиться электромагниты. Вращая маятник по часовой стрелке (см. рис.), зафиксировать его в верхнем положении при помощи левого (ближнего к стойке) электромагнита, при этом необходимо следить за тем, чтобы нить наматывалась на ось виток к витку. При вращении маятника против часовой стрелки фиксировать маятник необходимо при помощи правого (дальнего от стойки) электромагнита.
Нажать кнопку "СБРОС" для того, чтобы убедиться, что на табло устанавливаются нули.
2. При нажатии кнопки "ПУСК" на блоке электромагниты должны обесточиться, маятник должен начать раскручиваться, таймер должен произвести отсчет времени, а в момент пересечения маятником оптической оси фотодатчика отсчет времени должен прекратиться. Записать показания таймера, т.е. время движения маятника t1. При помощи визира по шкале вертикальной стойки определить ход маятника h1. Нажать кнопку "СБРОС". Привести маятник в исходное положение (зафиксировать в верхнем положении при помощи электромагнита).
2. Определить высоту h 2 и время t 2 подъема маятника. Для этого в конце подъема маятника после удара, в момент остановки, зажимают пальцами диск и измеряют при натянутых нитях значение высоты в верхнем положении стержня маятника по линейке; разность этого верхнего и нижнего отсчетов дает высоту h 2, на которую поднимается маятник. Затем повторяют опыт, пуская секундомер в момент удара и останавливая его в конце подъема; таким образом, определяется время подъема t 2.
Измерения величин t 1, t 2, h 1 и h 2 проводят не менее пяти раз. Результаты измерений заносятся в табл. 1.
Табл. 1. Экспериментальные данные.
| Номер опыта, i | h1, м | 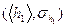 , м , м
| t1, с | 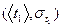 , c , c
| h2, м | 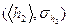 , м , м
| t2,c | 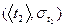 , с , с
|
При проведении измерений следует строго следить за правильностью положения оси маятника, избегать перекосов и срывов оси с нитей. Если в ходе эксперимента нити стали наматываться на ось с перехлестом или наоборот слишком разреженно, следует немедленно прекратить эксперимент. Необходимо помнить, что поврежденный маятник (с погнутой осью) не может быть использован в работе.
2. Обработка результатов
Величины h1,2 и t1,2 являются результатами прямых измерений, поэтому за оценку истинного значения измеряемой величины принимается выборочное среднее значение (среднее арифметическое по данной выборке). Выборка - число испытаний, в нашем случае n =5.
1. Провести вычисление средних значений 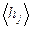 и
и 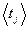 (j =1,2) по формулам:
(j =1,2) по формулам:
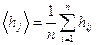
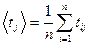
Результаты вычислений занести в табл. 1.
2. Провести оценку ошибок измеренных величин. В качестве оценки случайной погрешности среднего значения принимается выборочное стандартное отклонение среднего арифметического:
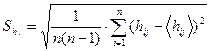
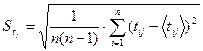
С учетом систематических погрешностей σсист. (погрешность прибора, погрешность округления и др.) величина стандартного отклонения суммарной погрешности физических величин hj и tj вычисляется следующим образом:
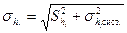
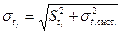
где S — выборочное стандартное отклонение среднего арифметического, σсист. - оценка суммарной систематической погрешности.
Полученные оценки погрешностей σ средних значений t 1, t 2, h 1 и h 2 также заносятся в табл. 1.
3. Величины ускорений маятника при спуске a 1 и подъеме a2 находят по формулам (5) и (9). Затем по формулам (7) и (8) определяют величины скоростей маятника до и после удара, v 1 и v 2, и коэффициент восстановления скорости Кв= v 1/ v 2.
4. Провести оценку ошибок полученных величин по формулам для косвенных измерений:
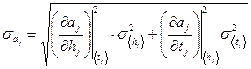
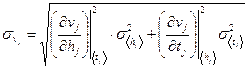
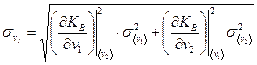
В соответствии с формулой (2), значения ускорений при спуске и подъеме маятника должны быть одинаковыми. Проверить совпадение ускорений a 1 и a 2 в пределах ошибок измерений.
Упражнение 2. Определение момента инерции маятника Максвелла.
1. С помощью формулы (6) провести вычисление момента инерции маятника Максвелла J.
2. Провести оценку ошибок полученного результата по формуле:
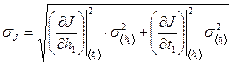
3. Используя данные о геометрических размерах маятника и плотностях материалов, из которых он изготовлен, рассчитать теоретическое значение момента инерции J теор.
Момент инерции маятника Максвелла складывается из моментов инерции стержня и диска. Таким образом, суммарный момент инерции системы относительно продольной оси имеет вид:
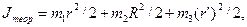
где r - радиуса стержня; R - радиус диска; r' - радиус утолщений на стержне; m 1, m 2, m 3 - массы стержня, диска и утолщений на стержне, соответственно. Массы различных частей маятника вычисляются исходя из их геометрических размеров и плотностей материалов, из которых они изготовлены.
4. Оценить погрешности полученного результата расчета J теор, используя формулы для оценки погрешностей в случае косвенных измерений.
5. Сравнить экспериментальное значение момента инерции с расчетным.
Основные итоги работы: в результате выполнения работы должны быть определены значения скоростей и ускорений маятника Максвелла на двух различных стадиях его движения (спуск и подъем). Кроме того, должен быть вычислен момент инерции маятника, экспериментально и теоретически, и проведено сравнение полученных результатов.
IV. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Сформулируйте определение плоского движения.
2. Что такое центр масс системы? Сформулируйте теорему о движении центра масс.
3. Дать определение момента инерции твердого тела.
4. Описать маятник Максвелла. Что является главным отличительным признаком маятника Максвелла? Почему это устройство называется маятником
5. Как изменяется кинетическая энергия системы в момент удара?
6. Получить выражение для момента инерции диска, кольца. Получите формулу для вычисления теоретического значения момента инерции маятника Максвелла.
7. Сформулируйте закон изменения импульса.
8. Сформулируйте закон изменения механической энергии.
9. Какое движение твердого тела называется плоским?
10. Как изменится ускорение и сила при увеличении момента инерции маятника?