СРЕДНИЕ ВЕЛИЧИНЫИ ПОКАЗАТЕЛИ ВАРИАЦИИ
1. Понятие средней величины
2. Виды средних величин и способы их вычисления
3. Структурные средние величины.
4. Показатели вариации
Понятие средней величины
Средняя величина – обобщающий показатель, характеризующий количественное значение признака в расчете на единицу изучаемой совокупности.
х = совокупность
Число единиц
Предприятие рассчитывает средние показатели, такие как среднесписочная численность работников, средняя з/п на одного работника, средний расход материалов на единицу продукции и т.д.
В статистике используют различные виды средних величин, которые делятся на два больших класса:
• степенные средние (средняя арифметическая, средняя хронологическая, средняя гармоническая);
• структурные средние (мода, медиана).
Основные свойства средней величины:
· Она обладает устойчивостью, что позволяет выявлять закономерности развития явлений.
· Она помогает характеризовать развитие уровня явления во времени.
· Она помогает выявить и охарактеризовать связь между явлениями.
Виды средних величин и способы их вычисления
В статистике используются различные виды средних величин. При их использовании важно правильно выбрать вид средней величины и способ ее расчета.
ü Средняя арифметическая простая - применяется в тех случаях, когда каждое индивидуальное значение признака встречается один или одинаковое кол-во раз
х = х1 +х2 +х3 + … + хп
n
где х1,х2...хn - индивидуальные значения варьирующего признака (варианты);
n - число единиц совокупности.
ü Средняя арифметическая взвешенная — вычисляется, когда даны различные меняющиеся показатели (варианты) и их повторяемость (частота) неодинакова:
|
|
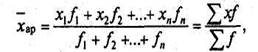
где х – варианта;
f — частота.
Средняя арифметическая взвешенная равна сумме произведений варианта на их частоты, поделенной на сумму частот.
Иногда среднюю арифметическую величину исчисляют по данным интервального вариационного ряда (когда варианта представлена в виде интервала). В этом случае в качестве значений признаков в группах принимают середины интервалов, в результате чего образуется дискретный ряд.
ü средняя хронологическая – применяется, когда необходимо рассчитать среднее значение материалов на складе, средние показатели по балансу:
х = х1/2 + х2 +х3 + … + хп/2
П – 1
ü средняя гармоническая взвешенная – если частота незвестна, а варианта и произведение этих вариант на частоты известны.
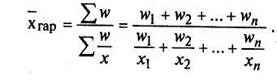
w = х * f
ü средняя гармоническая простая применяется в случаях определения средних затрат труда, времени и т.д.:
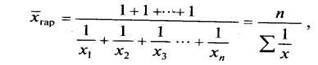
где х – отдельные варианты, n — их число.
Структурные средние величины.
Особым видом средних величин являются структурные средние. Они применяются для изучения внутреннего строения и структуры рядов распределения значений признака. К таким показателям относятся мода и медиана.
Мода M0 — это величина признака, которая чаще всего встречается в данной совокупности.
В дискретном вариационном ряду мода – это варианта с наибольшей частотой.
| Кол-во членов семьи, чел. | Кол-во чел. |
Решение. Модальной величиной в данном случае будет семья, в составе которой 4 человека, так как этому значению соответствует наибольшее число семей (260).
|
|
В интервальных рядах распределения с равными интервалами мода вычисляется по формуле:
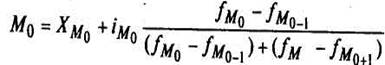
xМо – нижняя граница модального интервала;
iМо — величина модального интервала;
fМо – частота, соответствующая модальному интервалу;
fМо-1 – частота, предшествующая модальному интервалу;
fМо+1 – частота интервала, следующая за модальным.
Например, определить моду продолжительности стажа работы работников торгового предприятия:
| Группы работников по продолжительности стажа работы, лет | Число работников, чел. |
| До 3 | |
| 3 – 6 | |
| 6 – 9 | |
| 9 – 12 | |
| 12 и выше | |
| Итого |
Решение. Модальным интервалом величины стажа работников торгового предприятия будет интервал от 6 до 9 лет, так как этот интервал имеет наибольшую частоту (35 лет).
Тогда мода продолжительности стажа работников торгового предприятия составит:
Мо = 6+3 _____35 – 20 ______ = 7,2 года
(35 – 20) + (35 – 11)
Медиана Мe — это варианта, которая находится в середине вариационного ряда. Медиана делит ряд на две равные (по числу единиц) части.

xМе – нижняя граница медианного интервала;
i — величина интервала;
f – сумма частот;
SМе-1 – сумма накопленных частот до медианного интервала;
fМе – частота медианного интервала.
Решение. Медианным интервалом величины стажа работников торгового предприятия будет интервал от 6 до 9 лет, так как этот интервал имеет накопленную частоту.
Тогда медиана продолжительности стажа работников торгового предприятия составит:
|
|
Ме = 6+3 __80/2 – 27 __ = 7,1 года
Полученный результат говорит о том, что из 80 работников 40 имеют стаж менее 7,1 года, а 40 раб-в – более 7,1 года.
Мода и медиана широко используется при изучении покупательского спроса (при определении размеров одежды и обуви, которые пользуются широким спросом), регистрации цен; в демографии выявляются самый популярный (модальный) возраст вступления в брак, наиболее распространенные заболевания, уровень образования и т.д.
Показатели вариации
Средняя величина является обобщающей характеристикой признака изучаемой совокупности, но она не показывает строение совокупности. Показатели вариации рассчитываются для изучения величины их отклонений от средней величины.
Вариация признака – это несовпадение уровней одного и того же показателя у разных объектов.
Признаки, изучаемые статистикой, подвержены колебаниям. Так, в определенных пределах колеблется з/п отдельных рабочих, затраты труда на производство ед. прод. и.д. Для того, чтобы изучить их вариацию, измерить ее, вычисляют следующие показатели вариации:
ü Размах вариации
ü Среднее линейное отклонение
ü Дисперсия
ü Среднее квадратическое отклонение
ü Коэффициент вариации
ü Размах вариации - разность между максимальным и минимальным значением признака в изучаемой совокупности. Показывает, в каких пределах колеблется размер признака.
Представляет интерес, когда важно знать, какова амплитуда колебаний значений признака, например, каковы колебания цены на данный товар в течение недели или по разным регионам в данный отрезок времени. R = xmax - xmin
ü Среднее линейное отклонение (l) – средняя величина из отклонений индивидуальных значений признака от средней арифметической. Показывает на сколько в среднем каждое значение признака отклоняется от средней величины. С его помощью анализируется состав рабочих, ритмичность производства и т.д.
если совокупность не сгруппирована:
l = ∑ х - х
n
если сгруппирована, то по формуле средневзвешенной:
l = ∑ х – х f
∑ f
ü Дисперсия (σ2)– средний квадрат отклонений индивидуальных значений признака от средних величин.
если совокупность не сгруппирована:
σ2 = ∑ (х - х)2
n п- число вариант
если сгруппирована:
σ2 = ∑ (х - х)2f
∑ f
ü Среднее квадратическое отклонение (σ) – показывает во сколько раз в среднем колеблется величина признака совокупности. Чем оно меньше, тем точнее средняя арифметическая величина:
если совокупность не сгруппирована:
σ =√ ∑ (х - х)2
n
если сгруппирована: σ = √ ∑ (х - х)2 f
∑ f
ü Коэффициент вариации (V) – отношение среднего квадратического отклонения к средней арифметической величине. Позволяет судить об однородности совокупности: V= _σ_
x