| 1. Момент силы, приложенный к вращающемуся телу, изменяется по закону М = М0 – αt, где α - некоторая положительная константа. Момент инерции тела остается постоянным в течение всего времени вращения. Постройте график зависимости углового ускорения от времени. | |||||||
| 2. Диск вращается равномерно с некоторой угловой скоростью ω0. Начиная с момента времени t = 0, на него действует момент сил, график временной зависимости которого представлен на рисунке. Постройте график, правильно отражающий зависимость угловой скорости диска от времени. | 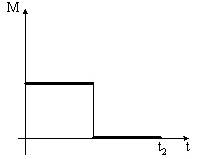
| ||||||
| 3. Момент силы, приложенный к вращающемуся телу, изменяется по закону М = αt, где α - некоторая положительная константа. Момент инерции тела остается постоянным в течение всего времени вращения. Постройте график зависимости углового ускорения тела от времени. | |||||||
| 4. Момент импульса тела относительно неподвижной оси изменяется по закону A) L = ct 3/2 B) L = at C) L = ct 3 D) L = ct 2. Постройте график, правильно отражающий зависимость от времени величины момента сил, действующих на тело. | |||||||
| 5. Диск начинает вращаться под действием момента сил, график временной зависимости которого представлен на рисунке. Постройте график, правильно отражающий зависимость момента импульса диска от времени. | 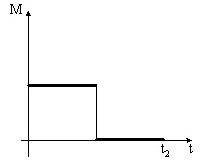
| ||||||
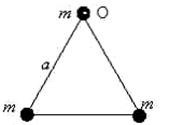
6. На рисунке изображена система трех точечных масс, расположенных в вершинах равностороннего треугольника со стороной 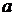 . Чему равен момент инерции системы относительно оси, проходящей через точку О перпендикулярно чертежу? . Чему равен момент инерции системы относительно оси, проходящей через точку О перпендикулярно чертежу?
| 
| ||||||
7. Ось вращения тонкого кольца перенесли из центра масс на расстояние 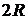 (рис.). Как изменится момент инерции относительно новой оси? (рис.). Как изменится момент инерции относительно новой оси?
| 
| ||||||
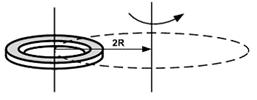
| 8. Ось вращения тонкостенной трубки перенесли из центра масс на образующую (рис.). Как изменится момент инерции относительно новой оси? | 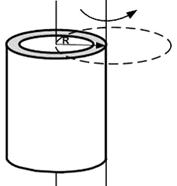
| ||||||
9. Как изменится момент инерции тонкого обруча, если ось вращения перенести параллельно в точку на обруче?
10. Чему равен момент инерции тонкого однородного стержня массой 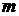 и длиной
и длиной 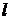 относительно оси, проходящей через его конец перпендикулярно стержню?
относительно оси, проходящей через его конец перпендикулярно стержню?
11. Вычислите момент инерции тонкого однородного стержня длиной 3 м и массой 10 кг относительно оси, перпендикулярной оси стержня на расстоянии 1/3 длины от его конца.
12. Момент импульса вращающегося тела изменяется по закону 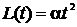 , где
, где 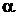 – некоторая положительная константа. Какова зависимость от времени момента сил, действующих на тело?
– некоторая положительная константа. Какова зависимость от времени момента сил, действующих на тело?
13. Величина момента импульса тела относительно неподвижной оси изменяется по закону 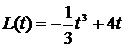 . Найдите зависимость величины момента сил, действующих на тело.
. Найдите зависимость величины момента сил, действующих на тело.
14. Как изменится момент импульса тела, если момент инерции тела и его скорость увеличить в 2 раза?
| 15.Тонкостенная трубка и кольцо, имеющие одинаковые массы и радиусы, вращаются с одинаковой угловой скоростью. Чему равно отношение величины момента импульса трубки к величине момента импульса кольца? | 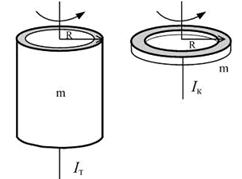
| |
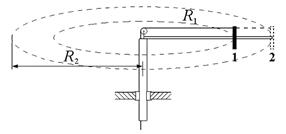
16. Вокруг неподвижной оси с угловой скоростью 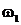 свободно вращается система из невесомого стержня и массивной шайбы, которая удерживается нитью на расстоянии свободно вращается система из невесомого стержня и массивной шайбы, которая удерживается нитью на расстоянии 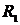 от оси вращения. Отпустив нить, шайбу перевели в положение 2. Найдите от оси вращения. Отпустив нить, шайбу перевели в положение 2. Найдите
| 
| |
угловую скорость шайбы при ее движении по окружности радиусом 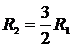 .
.
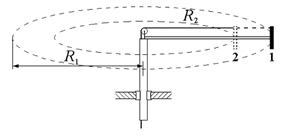
17. Вокруг неподвижной оси с угловой скоростью 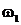 свободно вращается система из невесомого стержня и массивной шайбы, которая удерживается нитью на расстоянии свободно вращается система из невесомого стержня и массивной шайбы, которая удерживается нитью на расстоянии 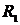 от оси вращения. Отпустив нить, шайбу перевели в положение 2. Найдите от оси вращения. Отпустив нить, шайбу перевели в положение 2. Найдите
| 
|
угловую скорость шайбы при ее движении по окружности радиусом  .
.
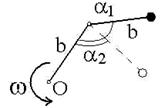
18. Два невесомых стержня длиной  каждый соединены под углом каждый соединены под углом 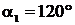 и вращаются без трения в горизонтальной плоскости вокруг вертикальной оси, проходящей через точку О, с угловой скоростью и вращаются без трения в горизонтальной плоскости вокруг вертикальной оси, проходящей через точку О, с угловой скоростью  . На конце одного из стержней прикреплен очень маленький массивный шарик. В . На конце одного из стержней прикреплен очень маленький массивный шарик. В
| 
|
некоторый момент угол между стержнями самопроизвольно уменьшился до 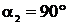 . Определите угловую скорость, с которой стала вращаться система.
. Определите угловую скорость, с которой стала вращаться система.
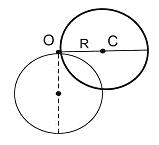
19. Тонкий обруч радиусом 1 м, способный свободно вращаться вокруг горизонтальной оси, проходящей через точку О перпендикулярно плоскости рисунка, отклонили от вертикали на угол 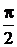 и отпустили. Определите угловое ускорение обруча в начальный момент времени. и отпустили. Определите угловое ускорение обруча в начальный момент времени.
| 
|
20. Определите момент инерции Земли относительно оси вращения, приняв ее за шар радиусом 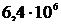 м и массой
м и массой 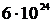 кг.
кг.
21. На барабан радиусом 0,5 м намотан шнур, к концу которого привязан груз массой 10 кг. Груз опускается с ускорением 2 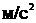 . Чему равен момент инерции барабана?
. Чему равен момент инерции барабана?
22. Величина момента импульса тела изменяется с течением времени по закону 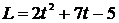 . Чему равен момент инерции тела, если в момент времени 2 с угловое ускорение составляет 3
. Чему равен момент инерции тела, если в момент времени 2 с угловое ускорение составляет 3  ?
?
23. Платформа, имеющая форму сплошного однородного диска, может вращаться по инерции вокруг неподвижной вертикальной оси. На краю платформы стоит человек, масса его в 3 раза меньше массы платформы. Определите, как и во сколько раз изменится угловая скорость движения платформы, если человек перейдет ближе к центру на расстояние, равное половине радиуса платформы.
24. Человек массой 80 кг стоит на краю горизонтальной платформы массой 100 кг, вращающейся по инерции с частотой 10 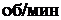 . Считая платформу диском, а человека – материальной точкой, определите частоту вращения платформы после того, как человек перейдет к ее центру.
. Считая платформу диском, а человека – материальной точкой, определите частоту вращения платформы после того, как человек перейдет к ее центру.
25. Однородный диск радиусом 0,2 м и массой 5 кг вращается вокруг оси, проходящей через его центр. Зависимость угловой скорости от времени описывается уравнением 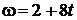 . Найдите величину касательной силы, приложенной к ободу диска. Трением пренебречь.
. Найдите величину касательной силы, приложенной к ободу диска. Трением пренебречь.
26. Однородный стержень длиной 1 м и массой 0,5 кг вращается в вертикальной плоскости вокруг горизонтальной оси, проходящей через середину стержня. С каким угловым ускорением вращается стержень, если вращающий момент равен 0,0981 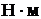 ?
?
27. По заданному уравнению вращения 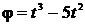 однородного цилиндра радиусом
однородного цилиндра радиусом 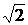 м и массой 60 кг определите вращающий момент внешних сил, действующих на него в момент времени 2 с.
м и массой 60 кг определите вращающий момент внешних сил, действующих на него в момент времени 2 с.
28. Однородный цилиндр массой 5 кг вращается вокруг своей оси по закону 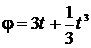 . Определите радиус цилиндра, если его вращение вызвано действием вращающего момента
. Определите радиус цилиндра, если его вращение вызвано действием вращающего момента 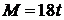 .
.
29. Вычислите момент импульса колеса велосипеда, движущегося со скоростью 18 км/ч. Масса и диаметр колеса равны соответственно 4 кг и 1 м.
30. Сплошной цилиндр массой 2 кг и радиусом 10 см вращается с угловой скоростью 10 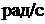 вокруг оси, совпадающей с одной из образующих цилиндрической поверхности. Найдите момент импульса цилиндра относительно его оси вращения.
вокруг оси, совпадающей с одной из образующих цилиндрической поверхности. Найдите момент импульса цилиндра относительно его оси вращения.
31. Тонкостенный цилиндр массой 2 кг и радиусом 0,3 м вращается вокруг своей оси с частотой 20 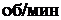 . Определите, с какой частотой он будет вращаться через 1 с после приложения вращающего момента внешних сил
. Определите, с какой частотой он будет вращаться через 1 с после приложения вращающего момента внешних сил 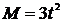 .
.
32. На блок радиусом 0,5 м намотан шнур, к концу которого привязан груз массой 10 кг. Найдите массу блока, если груз опускается с ускорением 2 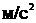 .
.
33. На какой угол повернется вокруг своей оси за 1 с однородный цилиндр, масса которого 1,5 кг и радиус 0,1 м, если он начал вращаться из состояния покоя под действием момента внешних сил 0,15 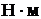 ?
?
34. Человек массой 80 кг спустился по лестнице длиной 5 м с высоты 4 м на поверхность земли. На сколько при этом уменьшилась его потенциальная энергия?
35. Мяч брошен вертикально вверх два раза. Второй раз ему сообщили скорость в 2 раза большую, чем в первый раз. Во сколько раз мяч поднимется выше при втором бросании?
36. Тело массой 2 кг бросили с поверхности земли вертикально ввверх со скоростью 20 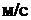 . Найдите максимальное значение его потенциальной энергии. Сопротивлением воздуха пренебречь.
. Найдите максимальное значение его потенциальной энергии. Сопротивлением воздуха пренебречь.
37. Тело массой 2 поднято над землей. Его потенциальная энергия 400 Дж. Определите скорость тела после прохождения 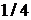 расстояния до земли. Сопротивлением воздуха пренебречь.
расстояния до земли. Сопротивлением воздуха пренебречь.
38. Тело массой 2 кг бросили с поверхности земли вертикально вверх со скоростью 20 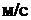 . Найдите значение его кинетической энергии после прохождения
. Найдите значение его кинетической энергии после прохождения  расстояния до точки максимального подъема. Сопротивлением воздуха пренебречь.
расстояния до точки максимального подъема. Сопротивлением воздуха пренебречь.
39. На частицу, находящуюся в начале координат, действует сила, вектор которой определяется выражением 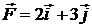 . Найдите работу, совершенную при перемещении частицы в точку с координатами (5; 0).
. Найдите работу, совершенную при перемещении частицы в точку с координатами (5; 0).
40. На частицу, находящуюся в начале координат, действует сила, вектор которой определяется выражением 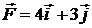 . Найдите работу, совершенную при перемещении частицы в точку с координатами (4; 3).
. Найдите работу, совершенную при перемещении частицы в точку с координатами (4; 3).
| 41. На рисунке показан вектор силы, действующей на частицу. Чему равна работа, совершенная этой силой при перемещении частицы из начала координат в точку с координатами (5; 2)? | 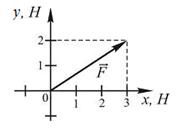
|
42. Обруч скатывается без проскальзывания с горки высотой 2,5 м. Определите скорость обруча у основания горки. Трением пренебречь.
43. Шар и полая сфера, имеющие одинаковые массы и радиусы, вкатываются без проскальзывания на горку с одинаковыми начальными скоростями. Какое из этих тел поднимется выше?
44. Сплошной и полый цилиндры, имеющие одинаковые массы и радиусы, скатываются без проскальзывания с горки высотой 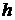 . Скорость какого тела будет больше у основания горки?
. Скорость какого тела будет больше у основания горки?
45. Сплошной и полый цилиндры, имеющие одинаковые массы и радиусы, скатываются без проскальзывания с горки с одной и той же высоты. Найдите отношение скоростей этих тел у основания горки. Трением и сопротивлением воздуха пренебречь.
46. Сплошной цилиндр и шар, имеющие одинаковые массы и радиусы, вкатываются без проскальзывания с одинаковыми скоростями на горку. Найдите отношение высот, на которые смогут подняться эти тела. Трением и сопротивлением воздуха пренебречь.
47. Обруч массой 0,3 кг и радиусом 0,5 м привели во вращение, сообщив ему энергию вращательного движения 1200 Дж, и опустили на пол так, что его ось вращения оказалась параллельной плоскости пола. Обруч начал двигаться без проскальзывания, имея кинетическую энергию поступательного движения 200 Дж. Определите работу силы трения.
48. Потенциальная энергия частицы задается функцией 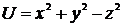 . Чему равна
. Чему равна 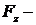 компонента вектора силы, действующей на частицу в точке А(1, 2, 3)?
компонента вектора силы, действующей на частицу в точке А(1, 2, 3)?
49. Потенциальная энергия частицы задается функцией  . Определите
. Определите 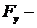 компоненту вектора силы, действующей на частицу в точке А(3, 1, 2).
компоненту вектора силы, действующей на частицу в точке А(3, 1, 2).
50. Потенциальная энергия частицы задается функцией 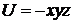 . Чему равна
. Чему равна  компонента вектора силы, действующей на частицу в точке А(1, 2, 3)?
компонента вектора силы, действующей на частицу в точке А(1, 2, 3)?
51. Потенциальная энергия частицы в некотором силовом поле задана функцией 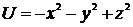 . Чему равна работа потенциальной силы по перемещению частицы из точки В(1, 1, 1) в точку С(2, 2, 2)?
. Чему равна работа потенциальной силы по перемещению частицы из точки В(1, 1, 1) в точку С(2, 2, 2)?
52. Частица движется в двумерном поле, причем ее потенциальная энергия задается функцией 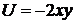 . Чему равна работа сил поля по перемещению частицы из точки С(1, 1, 1) в точку В(2, 2, 2).
. Чему равна работа сил поля по перемещению частицы из точки С(1, 1, 1) в точку В(2, 2, 2).
53. Стержень массой 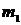 и длиной и длиной 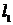 раскрутили вокруг вертикальной оси, проходящей перпендикулярно стержню через его середину, до угловой скорости раскрутили вокруг вертикальной оси, проходящей перпендикулярно стержню через его середину, до угловой скорости  , совершив при этом работу , совершив при этом работу 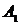 . До той же угловой скорости раскрутили стержень массой . До той же угловой скорости раскрутили стержень массой 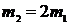 и длиной и длиной 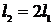 , совершив работу , совершив работу 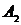 . Найдите отношение . Найдите отношение 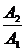 . .
| 
| ||
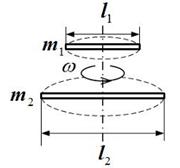
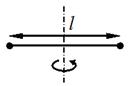
54. На концах невесомого стержня длиной 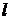 закреплены два маленьких массивных шарика. Стержень может вращаться в горизонтальной плоскости вокруг вертикальной оси, проходящей через середину стержня. Стержень раскрутили до угловой скорости закреплены два маленьких массивных шарика. Стержень может вращаться в горизонтальной плоскости вокруг вертикальной оси, проходящей через середину стержня. Стержень раскрутили до угловой скорости 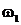 . .
| 
| ||
Под действием трения стержень остановился, при этом выделилось 4 Дж теплоты. Какое количество теплоты выделится при остановке стержня, если его раскрутить до угловой скорости 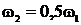 ?
?
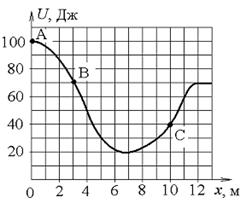
55. Небольшая шайба начинает движение без начальной скорости по гладкой ледяной горке из точки А. Сопротивление воздуха пренебрежимо мало. Зависимость потенциальной энергии шайбы от координаты 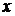 изображена на графике изображена на графике 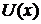 . Во сколько раз отличается кинетическая энергия шайбы в точке С от кинетической энергии в точке В? . Во сколько раз отличается кинетическая энергия шайбы в точке С от кинетической энергии в точке В?
| 
| |||
| 56. Тело движется под действием силы, зависимость проекции которой от координаты представлена на графике. Чему равна работа силы на пути 4 м? | 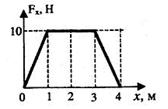
| |||
| 57. На рисунке показаны тела одинаковой массы и размеров, вращающиеся вокруг вертикальной оси с одинаковой частотой. Кинетическая энергия первого тела 0,5 Дж. Определите момент импульса второго тела, если масса каждого тела 1 кг, радиус – 10 см. | 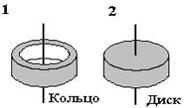
| |||
58. На рисунке показаны тела одинаковой массы и размеров, вращающиеся вокруг вертикальной оси с одинаковой частотой. Момент импульса первого тела 0,1 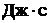 . Определите кинетическую энергию второго тела, если масса каждого тела 1 кг, радиус – 10 см. . Определите кинетическую энергию второго тела, если масса каждого тела 1 кг, радиус – 10 см.
| 
| |||
59. Материальная точка массой 100 г начинает двигаться под действием силы 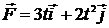 . Зависимость радиуса-вектора материальной точки от времени имеет вид
. Зависимость радиуса-вектора материальной точки от времени имеет вид 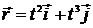 . Определите мощность, развиваемую силой в момент времени 1 с.
. Определите мощность, развиваемую силой в момент времени 1 с.
60. Частица совершила перемещение по некоторой траектории из точки 1 с радиус-вектором 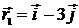 в точку 2 с радиус-вектором
в точку 2 с радиус-вектором 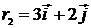 . При этом на нее подействовала сила
. При этом на нее подействовала сила 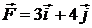 . Найдите работу, совершенную этой силой.
. Найдите работу, совершенную этой силой.
61. Тело массой 1 кг поднимают по наклонной плоскости. Высота наклонной плоскости 1 м, длина ее основания 2 м, коэффициент трения 0,2. Определите минимальную работу, необходимую для подъема тела.
62. Сила тяги автомобиля изменяется с расстоянием по закону F=D+Bs (D=200H;B=10H/м). Определить работу силы на участке пути (s1;s2), s1=50 м, s2=150 м.
63. Зависимость потенциальной энергии от координаты х задается в виде П(х)=-5х2+4х-3. Найти координату точки, соответствующей положению равновесия этой системы.
64. Вычислить кинетическую энергию диска массой 2 кг, катящегося без скольжения по горизонтальной поверхности со скоростью 2 м/с.
65. Железнодорожный вагон массой m, движущийся со скоростью ν, сталкивается с неподвижным вагоном массой 2m и сцепляется с ним. С какой скоростью движутся вагоны после столкновения?
66. Диск массой 1 кг и радиусом 30 см вращается вокруг оси, проходящей через центр перпендикулярно его плоскости, делая 20 об/с. Какую работу надо совершить, чтобы остановить диск?
67. Кинетическая энергия вала, вращающегося с постоянной скоростью, соответствующей 5 об/с, равна 60Дж. Найти момент импульса вала.
68. Мотор, делая 40 об/с, развивает мощность 3 КВт. Определить вращающий момент мотора.
69. Материальная точка движется прямолинейно по горизонтальной плоскости по закону s = Ct 4, где C = 1 м/с, под действием силы F=Bt 2, где B = 12 Н/с2. Определить работу этой силы по перемещению точки из начального положения в точку, где s = 4 м.
70. Якорь мотора вращается с частотой 1500 об./мин. Определить вращающий момент, если мотор развивает мощность 500 Вт.
71. Прямолинейное движение частицы массой 4 кг задано уравнением
s = 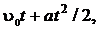 где
где 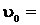 4 м/с, а = 4 м/с2. Определить кинетическую энергию частицы в момент времени t = 2 c.
4 м/с, а = 4 м/с2. Определить кинетическую энергию частицы в момент времени t = 2 c.
72. Маховик в виде сплошного диска массой 80 кг и радиусом 30 см находится в состоянии покоя. Какую работу нужно совершить, чтобы заставить маховик вращаться с частотой 600 об./мин.
73. Потенциальная энергия частицы является функцией ее координат: П(х,у,z) = Bx 3 + Cy 2 + Dz, где В = 4 Н/м2, С = 1 Н/м, D = 3 Н. Определить модуль вектора силы, действующей на частицу в точке с координатами
х = 0,5 м; у = z = 0.
74. Обруч и диск имеют одинаковую массу и катятся без скольжения с одинаковой скоростью. Кинетическая энергия обруча равна 40 Дж. Найти кинетическую энергию диска.
75. Однородный диск катится по горизонтальной плоскости со скоростью 5 м/с. На какую высоту он вкатится по наклонной плоскости за счет своей кинетической энергии? Трением пренебречь. (g =9,8 м/c2).
76. Тело массой 0,2 кг, брошенное с начальной скоростью 20 м/с с башни высотой 25 м, в момент удара о землю имело скорость 22 м/с.
Определить работу силы сопротивления воздуха.
77. Из ствола орудия массой 5 т вылетает снаряд массой 100 кг. Кинетическая энергия снаряда на вылете 7,5 МДж. Какую кинетическую энергию получает орудие?
78. Конькобежец массой 70 кг, стоя на коньках на льду, бросает в горизонтальном направлении камень массой 3 кг со скоростью 8 м/с. На какое расстояние откатится при этом конькобежец, если коэффициент трения коньков о лед равен 0,02?