Типовой расчет
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
Задача №1. Построение математических моделей задач линейного программирования
Условие задачи №1
Задача о выборе оптимальных технологий
Продукция в цехе может производиться n различными способами Tj (n =3). Для производства продукции могут использоваться ресурсы: рабочая сила, сырьё (сталь, древесина, цветные металлы), электроэнергия. Обозначения:
x j – время использования технологического способа Tj при производстве продукции (j =1,2,3);
b i – объем ресурса R i (i =1,2,3);
a ij – расход ресурса Ri за единицу времени по технологии Tj;
A – годовое плановое задание по выработке продукции (ден. ед.);
cj – производительность технологии Tj (в денежных единицах за единицу времени работы по данной технологии);
l j – затраты на изготовление продукции в единицу времени по технологии Tj (денежных единицах).
Налагаются ограничения по объемам b i ресурсов (вида £) и по плановому выпуску A продукции (вида ³).
Возможны три критерия f 1, f 2, f 3 оптимальности плана X =(x 1,…, xn) применения каждого технологического способа:
а) f 1 – наибольший объем выпускаемой продукции по всем технологиям (ден. ед.);
б) f 2 – наименьшие затраты на выполнение планового задания (ден. ед.);
в) f 3 – наибольшая конечная прибыль от выпуска продукции с учетом затрат на изготовление продукции (ден. ед.).
В табл. 1 представлены объемы b i ресурсов R i, их расход aij в единицу времени для каждой технологии, плановое задание A, производительности c j технологий T j и затраты l j.
Задание
1. Заполнить таблицу 1 числовыми данными своего варианта и составить математические модели задачи по трем критериям оптимальности, сопровождая построение подробными пояснениями.
2. Дать математические постановки задач.
3. Привести полученные три математические модели к каноническому виду. Указать экономический смысл дополнительных (балансовых) переменных.
Таблица 1.
| Ресурсы | Технологические способы | Объем ресурсов | ||
| T 1 | T 2 | T 3 | ||
| Рабочая сила, чел-ч | ||||
| Сырье, т | ||||
| Электроэнергия, кВт ч | ||||
| Производительность технологического способа, ден. ед. | ||||
| Затраты в ед. времени работы по технологическому способу, ден. ед. |
Решение
а) Пусть требуется реализовать первый критерий f 1 оптимальности плана X =(x 1,…, xn), т.е. объем выпускаемой продукции по всем технологиям должен быть наибольшими. Поскольку x 1, x 2, x 3 время использования технологического способа T 1, T 2, T 3, соответственно, то объем использования каждого ресурса в соответствии с таблицей будет равен:
| рабочей силы | 3 x 1 + 4 x 2 + 4 x 3, |
| сырья | 4 x 1 + 3 x 2 + 3 x 3, |
| электроэнергии | 3 x 1 + x 2 + 4 x 3. |
При этом потребление каждого ресурса не должно превышать их объемов, т.е. 350, 850, 720, соответственно. Таким образом, связь между потреблением ресурсов и их объемами выражается следующей системой неравенств:
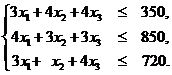 (1)
(1)
Учитывая производительность каждого технологического способа, найдем объем всей выпускаемой продукции
 (2)
(2)
Добавляя сюда условия неотрицательности
 (3)
(3)
можно дать формулировку математической модели задачи:
Требуется найти такой план использования технологических способов X =(x1, x2, x3), удовлетворяющий системе (1) и условиям (3), при которых целевая функция (2) принимает максимальное значение.
Поскольку система (1) содержит три неравенства, то для того, чтобы перейти к равенствам, введем в левую часть неравенств три дополнительных неотрицательных переменных. В результате, исходная задача в каноническом виде запишется следующим образом: найти максимум целевой функции (2) при ограничениях
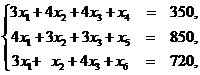 (4)
(4)
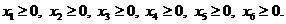
Новые переменные имеют следующий смысл: x 4 – количество неиспользуемой рабочей силы, x 5 – количество неиспользуемого сырья, x 6 – количество неиспользуемой электроэнергии.
б) Пусть требуется реализовать второй критерий f 2 оптимальности плана X =(x 1,…, xn), т.е. затраты на выполнение планового задания должны быть наименьшими. В отличие от выше рассмотренной задачи, здесь добавляется дополнительное условие, т.е. кроме ограничений по объемам ресурсов налагаются условия по плановому выпуску продукции. Учитывая производительность каждого технологического способа и годовое плановое задание по выработке продукции, по данным табл. 1 получим ограничение 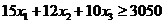 . Таким образом, система ограничений будет иметь вид
. Таким образом, система ограничений будет иметь вид
 (5)
(5)
 (6)
(6)
С учетом затраты в единицу времени работы по технологическому способу, целевая функция (затраты на выполнение планового задания) будет иметь вид
 (7)
(7)
Дадим теперь формулировку математической модели задачи:
Требуется найти такой план использования технологических способов X =(x1, x2, x3), удовлетворяющий системе (5) и условиям (6), при которых целевая функция (7) принимает минимальное значение.
Поскольку система (5) содержит четыре неравенства, то для того, чтобы перейти к равенствам, введем в левую часть неравенств четыре дополнительных неотрицательных переменных, однако в четвертое неравенство переменную нужно ввести со знаком минус. В результате, исходная задача в каноническом виде запишется следующим образом: найти минимум целевой функции (7) при ограничениях
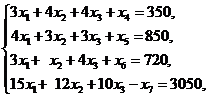 (8)
(8)

Новые переменные имеют следующий смысл: x 4 – количество неиспользуемой рабочей силы, x 5 – количество неиспользуемого сырья, x 6 – количество неиспользуемой электроэнергии, x 7 – количество продукции, выработанной сверх плана.
в) Пусть требуется реализовать третий критерий f 3 оптимальности плана X =(x 1,…, xn), т.е. конечная прибыль от выпуска продукции с учетом затрат на изготовление продукции должна быть наибольшей. В отличие от случая а), целевая функция будет иметь вид
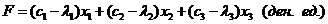 ,
,
или, учитывая данные таблицы,
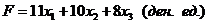 . (9)
. (9)
Тогда математическая модель задачиформулируется следующим образом:
Требуется найти такой план использования технологических способов X =(x1, x2, x3), удовлетворяющий системе (1) и условиям (3), при которых целевая функция (9) принимает максимальное значение.
В каноническом виде задача формулируется следующим образом: найти максимум целевой функции (9) при ограничениях
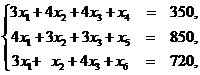 (10)
(10)
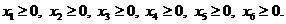
Новые переменные имеют следующий смысл: x 4 – количество неиспользуемой рабочей силы, x 5 – количество неиспользуемого сырья, x 6 – количество неиспользуемой электроэнергии.
Задача №2. Графическое решение задачи линейного программирования
Условие задачи №2