На предприятии выпускается n видов P j (j =1, 2,…, n). При ее изготовлении используются ресурсы R 1, R 2, R 3, размеры допустимых затрат ресурсов ограничены величинами b 1, b 2, b 3. Расход ресурса R i (i =1,2,3) на производство единицы продукции Pj равен a ij. Прибыль от реализации единицы продукции Pj равна cj ден. ед.
Необходимо найти оптимальный план выпуска продукции каждого вида с учетом имеющихся ограниченных ресурсов, который обеспечивал бы предприятию максимальную прибыль.
Задание
1. Записать математическую модель задачи.
2. Привести модель к каноническому виду и заполнить симплексную таблицу.
3. Построить исходное опорное решение, проверить его на оптимальность и, последовательно улучшая с помощью симплексных преобразований, найти оптимальное решение X опт и f наиб (X опт).
4. Дать экономическое истолкование оптимального решения X опт и наибольшего значения целевой функции f наиб (X опт).
Решение
Исходные данные запишем в виде таблицы
Таблица 3.
| Сырье | Продукция | Запасы сырья | |||
| P 1 | P 2 | P 3 | P 4 | ||
| R 1 | |||||
| R 2 | |||||
| R 3 | |||||
| Прибыль от реализации единицы продукции, cj, ден. ед. | 0,4 | 0,2 | 0,5 | 0,8 |
Таким образом, математическую модель задачи можно сформулировать следующим образом:
Требуется найти такой план выпуска продукции X =(x1, x2, x3, x4), удовлетворяющий системе
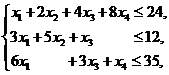 (14)
(14)
и условиям
 (15)
(15)
при которых целевая функция
 (16)
(16)
принимает максимальное значение.
Перейдем к каноническому виду системы ограничений:


В качестве базисных переменных выбираем переменные x 5, x 6, x 7. Приравняв нулю свободные переменные x 1= x 2= x 3= x 4=0, получим первоначальный опорный план:
 .
.
Для проверки на оптимальность этого опорного плана составим первую симплекс-таблицу:
| Базис | Cб | B | |||||||||||
| A 1 | A 2 | A 3 | A 4 | A 5 | A 6 | A 7 | |||||||
| A 5 | 2,5 | 2,5 | 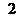
| 1,5 |
  0 0
| ||||||||
| A 6 |
 0 0
| ||||||||||||
| A 7 |  1 1
| ||||||||||||
| F 0=0 | –40 | –50 | –100 | –80 |  0 0
|
Оценочная строка вычисляется следующим образом: F 0= Cб × B =0, D1= Cб × A 1– c 1=
–40, D2= Cб × A 2– c 2=–50, D3= Cб × A 3– c 3=–100, D4= Cб × A 4– c 4=–80. Для базисных векторов оценки равны нулю.
Поскольку все оценки D j отрицательные, следовательно, первоначальный план не является оптимальным. В качестве разрешающего элемента выберем число 2, стоящее на перекрестке третьего столбца (в этом столбце самая маленькая оценка, –100) и первой строки (здесь 100/2<260/4<370/4). Это означает, что вектор A 3 нужно включить в базис, а вектор A 5 исключить. Составим новую симплекс-таблицу. Для этого все элементы разрешающей строки разделим на 2 и с помощью этой строки получим нули в разрешающем столбце, т.е. прибавим первую преобразованную стоку ко второй, предварительно умножив ее на –4, и т.д.
| Базис | Cб | B | |||||||||
| A 1 | A 2 | A 3 | A 4 | A 5 | A 6 |
| |||||
| A 3 | 1,25 | 1,25 | 0,75 | 0,5 |
  0 0
| ||||||
| A 6 | –1 | 
| –2 |
 0 0
| |||||||
| A 7 | –2 |  | |||||||||
| F 1=5000 | –5 |  0 0
|
Во второй симплекс-таблице получен новый опорный план:
 ,
,
которому соответствует новое значение целевой функции F 1= F (X 1)=5000. Однако в последней строке есть отрицательная оценка, следовательно, полученный опорный план не является еще оптимальным.
Преобразуем симплекс-таблицу еще раз. Для этого в качестве разрешающего элемента возьмем число 7, стоящее на перекрестке четвертого столбца (в этом столбце находится отрицательная оценка) и второй строки (здесь 60/3<170/7<50/0,75). Таким образом, вектор A 6 исключается из базиса, а вектор A 4 включается. Составляем новую симплекс-таблицу.
| Базис | Cб | B | |||||||
| A 1 | A 2 | A 3 | A 4 | A 5 | A 6 | A 7 | |||
| A 3 | 1,5 | –0,25 | |||||||
| A 4 | –1/3 | 5/3 | –2/3 | 1/3 | |||||
| A 7 | 28/3 | –19/3 | 8/3 | –7/3 | |||||
| F 1=5100 | 250/3 | 250/3 | 140/3 | 5/3 |
Итак, в последней строке все оценки положительные. Следовательно, опорный план
 ,
,
является оптимальным и ему соответствует значение целевой функции Fmax = F (X 2)=5100.
Таким образом, для того чтобы предприятию получить максимальную прибыль нужно выпускать 35 ед. продукции П 3 и 20 ед. продукции П 4, а продукцию П 1 и П 2 вообще не выпускать. При таком плане ресурсы R 1 и R 2 будут реализовываться полностью, а ресурс R 3 будет реализовываться не полностью, здесь будет оставаться остаток 30 ед. При осуществлении такого плана, предприятие получит наибольшую прибыль в размере 5100 ден. ед.
Задача №4. Двойственные задачи
Условие задачи №4
Для задачи о выборе оптимальных технологий (см. задачу №3) требуется:
1. Сформулировать в экономических терминах двойственную задачу.
2. Составить математическую модель двойственной задачи, указав смысл двойственных переменных системы ограничений и целевой функции.
3. Используя оптимальное решение X опт задачи №3 и соответствие между парами двойственных переменных прямой и двойственной задач, найти компоненты оптимального решения Y опт двойственной задачи и значение целевой функции T min в двойственной задаче.
4. Дать экономическое истолкование величине T min, значениям  основных и дополнительных переменных в оптимальном решении Y опт двойственной задачи. Указать наиболее дефицитный и недефицитный (избыточный) ресурсы, если они имеются.
основных и дополнительных переменных в оптимальном решении Y опт двойственной задачи. Указать наиболее дефицитный и недефицитный (избыточный) ресурсы, если они имеются.
5. Пусть ресурсы взаимозаменяемы и из производства исключается D b 1=2 единицы ресурса R 1. Определить на сколько может уменьшиться максимальный доход (величина D1 fmax). Найти, сколько единиц ресурсов R 2 и R 3 нужно ввести дополнительно в производство, чтобы компенсировать возможный убыток.
Решение
Двойственную задачу можно сформулировать следующим образом. Найти такой набор цен ресурсов Y, при котором общие затраты на ресурсы будут минимальными, при условии, что затраты на ресурсы при производстве каждого вида продукции будут не менее прибыли (выручки) от реализации этой продукции.
Составим математическую модель двойственной задачи. Выпишем расширенную матрицу системы, в которую включим основную матрицу системы A, столбец свободных членов B и строку коэффициентов целевой функции C:


 .
.
Транспонируем матрицу A 1:


 .
.
Сформулируем двойственную задачу на основании полученной матрицы  и условия неотрицательности переменных. Найти такой набор цен ресурсов Y =(y1,y2,y3), при котором общие затраты на ресурсы (целевая функция) будут минимальными
и условия неотрицательности переменных. Найти такой набор цен ресурсов Y =(y1,y2,y3), при котором общие затраты на ресурсы (целевая функция) будут минимальными

при условии, что затраты на ресурсы при производстве каждого вида продукции будут не менее прибыли (выручки) от реализации этой продукции


Если прямая ЗЛП имеет оптимальный план X, то Y = C бD –1 является оптимальным планом двойственной задачи. Здесь C б =(c 1, c 2, …, cr) – вектор-строка, составленная из коэффициентов при базисных переменных целевой функции; D –1 – матрица, обратная матрице D, составленной из компонент векторов A 1, A 2,…, Ar. таким образом. если найти симплекс-методом оптимальный план прямой задачи, то зная C б и D –1 можно найти оптимальный план двойственной задачи. Для определения C б и D –1 можно использовать последнюю симплекс-таблицу. Более тог, по этой таблице можно сразу определить произведение C бD –1, поскольку компоненты этого плана совпадают с соответствующими элементами последней оценочной строки плюс cj, т.е. yj= D j+cj.
В последней симплекс-таблице задачи №3 базисом являются векторы A 3, A 4, A 7, тогда по первой симплекс-таблице находим
 .
.
Обратная матрица D–1 образуется из коэффициентов последней симплекс-таблице, стоящих в столбцах A 5, A 6, A 7 (являющихся единичными в исходной симплекс-таблице):
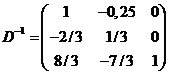 .
.
Поскольку, в соответствие с симплекс-таблицей, Cб =(100; 80; 0), то
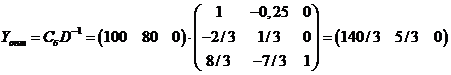 ,
,
т.е. компоненты оптимального плана двойственной задачи находятся в оценочной строке последней симплекс-таблицы, стоящие в столбцах векторов первоначального единичного базиса.
В соответствии с первой теоремой двойственности, если одна из пары двойственных задач обладает оптимальным планом, то и другая обладает оптимальным планом, причем Fmax=Tmin. В нашем случае
 ,
,
т.е. общие затраты на ресурсы при производстве каждого вида продукции при оптимальном плане совпадает прибылью от реализации этой продукции.
Сырье R 1 и R 2 по оптимальному плану полностью использовано (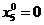 ,
,  ) и объективно обусловленные оценки этого сырья ненулевые (
) и объективно обусловленные оценки этого сырья ненулевые ( ,
,  ), а сырье R 3 использовано не полностью используется в оптимальном плане (
), а сырье R 3 использовано не полностью используется в оптимальном плане ( ) и объективно обусловленная оценка этого сырья нулевая (
) и объективно обусловленная оценка этого сырья нулевая ( ).
).
Таким образом, сырье R 1 и R 2 будет дефицитным (т.е. полностью используемым). При этом сырье R 1 будет наиболее дефицитным, т.к. ее оценка самая высокая. Сырье R 3 будет не дефицитным и поэтому ее оценка равна нулю.
Дополнительные переменные двойственной задачи y 4, y 5, y 5, y 6, представляют разность между затратами на сырье для производства из них единицы продукции и ценами cj продукции P j. По оптимальному плану в исходной задаче следует производить только продукцию P 3 и P 4 ( ,
, 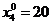 ) и превышение затрат на сырье над ценой реализации равно нулю, т.е. дополнительные переменные
) и превышение затрат на сырье над ценой реализации равно нулю, т.е. дополнительные переменные  ,
,  .
.
Если из производства исключается D b 1=2 единиц продукции R 1, то максимальный доход уменьшится на величину
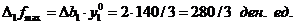
Поскольку  , а
, а  , то для компенсации возможного убытка в производство нужно ввести дополнительно
, то для компенсации возможного убытка в производство нужно ввести дополнительно

единиц ресурса R 2.
Задача №5. Транспортная задача
Условие задачи №5
На заводах A 1, A 2, A 3 производится однородная продукция в количестве a 1, a 2, a 3 единиц. Себестоимость единицы продукции на заводе A i составляет ci ден. единиц.
Четырем потребителям B 1, B 2, B 3, B 4 требуется соответственно b 1, b 2, b 3, b 4 единиц готовой продукции. Расходы cij ден. ед. по перевозке единицы готовой продукции с завода A i потребителю B j заданы.
Необходимо найти план перевозок, минимизирующий общие затраты по изготовлению продукции на A 1, A 2, A 3 и ее доставке потребителям B 1, B 2, B 3, B 4.
Задание
1. Внести числовые данные транспортной задачи в распределительную таблицу и составить математическую модель.
2. Если транспортная задача открытого типа, то привести ее к закрытой. Построить исходные планы перевозок по методы "северо-западного угла" (X с-з) и по методу "минимального элемента" (X мэ). Вычислить значения общих затрат для построенных планов f (X с-з) и f (X мэ) и выявить, какой планов лучше.
3. Методом потенциалов проверить этот план X на оптимальность.
4. Последовательно улучшая план перевозок X с помощью циклов пересчета в распределительной таблице, найти оптимальный план перевозок X опт.
5. Определить по оптимальному плану перевозок X опт:
1) количество продукции, отправляемое из каждого завода A 1, A 2, A 3 каждому потребителю B 1, B 2, B 3, B 4;
2) наименьшие общие затраты на производство продукции и доставку ее потребителям;
3) заводы A i, в которых остается нераспределенная продукция, и указать ее объем;
4) Пункты потребления B j, которые недополучают продукцию, и указать ее количество.
Решение
Составим распределительную таблицу транспортной задачи:
Таблица 4.
| Пункты отправления | Потребители | Количество произведенной продукции, ai | |||
| B 1 | B 2 | B 3 | B 4 | ||
| A 1 | x 11 | x 12 | x 13 | x 14 | |
| A 2 | x 21 | x 22 | x 23 | x 24 | |
| A 3 | x 31 | x 32 | x 33 | x 34 | |
| Потребности в готовой продукции, bj |
Транспортная задача ставится следующим образом: Найти объемы перевозок для каждой пары "поставщик-потребитель" так, чтобы:
1) мощности всех поставщиков были реализованы;
2) спросы всех потребителей были удовлетворены;
3) суммарные затраты на перевозку были бы минимальными.
Построим математическую модель данной задачи. Пусть xij – объем перевозки от i -го поставщика к j -му потребителю. Тогда, чтобы мощность каждого из поставщиков была реализована, необходимо составить уравнения баланса для каждой строки таблицы распределений:
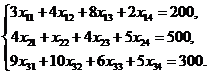
Аналогично, чтобы спрос каждого из потребителей был удовлетворен, подобные уравнения баланса составляем для каждого столбца таблицы:

Очевидно, что объем перевозимого груза не может быть отрицательным, поэтому следует дополнительно предположить, что
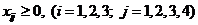 .
.
Суммарные затраты F выражаются через коэффициенты затрат на перевозку и себестоимость единицы продукции на каждом заводе:

Данная транспортная задача является задачей открытого типа, поскольку общее количество произведенной продукции  не совпадает с общими потребностями потребителей
не совпадает с общими потребностями потребителей  . Однако эту задачу можно свести к задаче закрытого типа, если ввести фиктивного потребителя B 5, потребности которого равны b 5=100. Стоимость перевозок единицы груза фиктивного потребителя полагается равным нулю, т.к. груз в этом случае не перевозится. С учетом себестоимости единицы продукции на каждом целевая функция примет вид
. Однако эту задачу можно свести к задаче закрытого типа, если ввести фиктивного потребителя B 5, потребности которого равны b 5=100. Стоимость перевозок единицы груза фиктивного потребителя полагается равным нулю, т.к. груз в этом случае не перевозится. С учетом себестоимости единицы продукции на каждом целевая функция примет вид
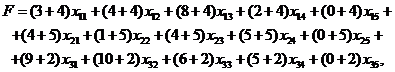
т.е.

В результате распределительная таблица транспортной задачи примет вид:
Таблица 5.
| Продукция | Потребители | Количество произведенной продукции, ai | ||||
| B 1 | B 2 | B 3 | B 4 | B 5 | ||
| A 1 | x 11 | x 12 | x 13 | x 14 | x 14 | |
| A 2 | x 21 | x 22 | x 23 | x 24 | x 24 | |
| A 3 | x 31 | x 32 | x 33 | x 34 | x 34 | |
| Потребности в готовой продукции, bj | 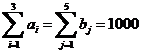
|
Найдем первоначальный план полученной задачи методом северо-западного угла. Поскольку число пунктов отправления m =3, а число пунктов назначения n =5, то опорный план задачи определяется числами, стоящими в 5+3–1=7 клетках.
Заполнение таблицы начнем с клетки для переменной x 11, т.е. попытаемся удовлетворить потребности первого пункта назначения за счет запасов первого пункта отправления. Полагаем x 11= min (150,200)=150. после этого спрос потребителя B 1 будет полностью удовлетворен, в результате чего столбец B 1 выпадет из последующего рассмотрения. Далее будем учитывать, что запасы пункта A 1 уменьшились и стали равными 200–150=50. После того, как мы вычеркнули столбец B 1, найдем новый "северо-западный" угол. Это будет клетка с переменной x 12. С учетом того, что запасы A 1 уменьшились, положим x 12= min (450,50)=50. После этого выпадает из рассмотрения строка A 1, поскольку количество продукции завода A 1 полностью исчерпываются. Далее переходим к клетке с переменной x 22 и т.д. Процесс продолжаем до тех пор, пока не дойдем до клетки x 35.
Таблица 6.
| Продукция | Потребители | Количество | ||||
| B 1 | B 2 | B 3 | B 4 | B 5 | продукции | |
| A 1 | ||||||
| A 2 | ||||||
| A 3 | ||||||
| Потребности | 1000=1000 |
В результате получаем опорный план
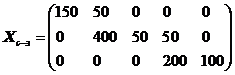
Согласно данному плану перевозок, общая стоимость перевозок продукции составит
 .
.
Найдем первоначальный план полученной задачи методом минимального элемента. Заполнение таблицы начнем с клетки с минимальным тарифом, т.е. с клетки для переменной x 35 в которой тариф равен 2. Положим x 35=100 и исключим из рассмотрения столбец B 5. Запасы A 3 станут равны 200. После этого рассмотрим оставшуюся часть таблицы. В ней минимальный тариф находится в клетках с переменными x 22. Выберем клетку x 14 и заполним ее, т.е. положим x 14=200 и исключим из рассмотрения строку A 1. Продолжая этот процесс, получим первоначальный план.
Таблица 7.
| Продукция | Потребители | Количество | ||||
| B 1 | B 2 | B 3 | B 4 | B 5 | продукции | |
| A 1 | ||||||
| A 2 | ||||||
| A 3 | ||||||
| Потребности | 1000=1000 |
В результате получаем опорный план

Согласно данному плану перевозок, общая стоимость перевозок продукции составит
 .
.
В результате получилось, что опорные планы, полученный методом "северо-западного угла" и методом минимального элемента получились равноценными.
Проверим опорный план, полученный методом минимального элемента, на оптимальность методом потенциалов. Для этого для каждого из пунктов отправления A i и назначения B j определим потенциалы ui и vj. Эти числа находятся из уравнений ui + vj = cij, где cij – тарифы, стоящие в заполненных клетках таблицы. Пусть u 1=0, тогда v 4=6. Отсюда находим u 3=1 и т.д.
Если первоначальный опорный план является оптимальным, то для каждой незанятой клетки должно выполняться условие ui + vj £ cij. Если хотя бы одна незанятая клетка не удовлетворяет этому условию, то опорный план не является оптимальным. Поэтому для каждой свободной клетки найдем числа
 .
.
Таблица 8.
| Матрица планирования | Потребители | Запасы | |||||||||
| B 1 | B 2 | B 3 | B 4 | B 5 | |||||||
| Поставщики | vj ui |
| |||||||||
| A 1 |
| –1 | –5 |
 200 200
| –3 | ||||||
| A 2 | –1 | –3 | –5 | –5 | |||||||
| A 3 |
| –4 |
| ||||||||
| Потребности | 1000=1000 |
Поскольку a11=3>0, то полученный опорный план не является оптимальным. Улучшим первоначальный опорный план методом циклов. Выберем свободную клетку, для которой a ij >0. Такая клетка только одна: x 11. Строим для нее цикл (см., табл. 8). Делаем перерасчет по циклу. 1) Каждой вершине цикла присваиваем знак "+" или "–" следующим образом: свободной клетке – знак плюс, а дальше расставляют знаки так, чтобы они от вершины к вершине чередовались. 2) Находим q0=min xij, где xij – перевозки, стоящие в вершинах цикла, отмеченных знаком "–". В нашем случае q0=100. 3) Значение q0 записываем в незанятую клетку, далее двигаясь по циклу, вычитаем q0 из объемов перевозок, расположенных в клетках, отмеченных знаком минус, и прибавляем q0 к объемам перевозок, которые отмечены знаком плюс. В результате получаем новы опорный план, который проверяем на оптимальность, т.е. заполним новую таблицу распределений.
Таблица 9.
| Матрица планирования | Потребители | Запасы | |||||
| B 1 | B 2 | B 3 | B 4 | B 5 | |||
| Поставщики | vj ui | ||||||
| A 1 | –4 | –5 | –3 | ||||
| A 2 | –2 | –2 | |||||
| A 3 | –3 | –7 | |||||
| Потребности | 1000=1000 |
Поскольку для всех свободных клеток a ij £0, то полученный опорный план является оптимальным:

Согласно данному плану перевозок, наименьшие общие затраты на производство продукции и доставку ее потребителям составят
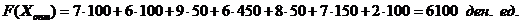
Согласно полученному оптимальному плану с завода A 1 отправляется по 100 ед. продукции потребителям B 1 и B 4; с завода A 2 отправляется 50 ед. продукции потребителю B 1; с завода A 3 отправляется 50 ед. продукции потребителюпо B 3, 150 ед. продукции потребителю B 4 и 100 ед. продукции фиктивному потребителю B 5.
Поскольку количество произведенной продукции превышают потребности в готовой продукции, то часть продукции останется нераспределенной. Согласно полученному оптимальному плану, продукция завода A 3 не вся будет распределена, объем нераспределенной продукции составит 100 ед. В то время как потребители полностью удовлетворят свои потребности.
