Свойства степеней с целыми показателями

Так как целые положительные числа есть натуральные числа, то все свойства степеней с целыми положительными показателями в точности совпадают со свойствами степеней с натуральными показателями, перечисленными и доказанными в предыдущем пункте.

Степень с целым отрицательным показателем, а также степень с нулевым показателем мы определяли так, чтобы оставались справедливыми все свойства степеней с натуральными показателями, выражаемые равенствами. Поэтому, все эти свойства справедливы и для нулевых показателей степени, и для отрицательных показателей, при этом, конечно, основания степеней отличны от нуля.

Итак, для любых действительных и отличных от нуля чисел a и b, а также любых целых чисел m и n справедливы следующие свойства степеней с целыми показателями:

1. a^m·aⁿ=a^m+n;

2. a^m:aⁿ=a^m−n;

3. (a·b)ⁿ=aⁿ·bⁿ;

4. (a:b)ⁿ=aⁿ:bⁿ;

5. (a^m)ⁿ=a^m·n;

6. если n – целое положительное число, a и b – положительные числа, причем a<b, то aⁿ<bⁿ и a⁻ⁿ>b⁻ⁿ;

7. если m и n – целые числа, причем m>n, то при 0<a<1 справедливо неравенство a^m<aⁿ, а при a>1 выполняется неравенство a^m>aⁿ.

При a=0 степени a^m и aⁿ имеют смысл лишь когда и m, и n положительные целые числа, то есть, натуральные числа. Таким образом, только что записанные свойства также справедливы для случаев, когда a=0, а числа m и n – целые положительные.

Доказать каждое из этих свойств не составляет труда, для этого достаточно использовать определения степени с натуральным и целым показателем, а также свойства действий с действительными числами. Для примера докажем, что свойство степени в степени выполняется как для целых положительных чисел, так и для целых неположительных чисел. Для этого нужно показать, что если p есть нуль или натуральное число и q есть нуль или натуральное число, то справедливы равенства (a^p)^q=a^p·q, (a^−p)^q=a^(−p)·q, (a^p)^−q=a^p·(−q) и (a^−p)^−q=a^{(−p)·(−q)}. Сделаем это.

Для положительных p и q равенство (a^p)^q=a^p·q доказано в предыдущем пункте. Если p=0, то имеем (a⁰)^q=1^q=1 и a^0·q=a⁰=1, откуда (a⁰)^q=a^0·q. Аналогично, если q=0, то (a^p)⁰=1 и a^p·0=a⁰=1, откуда (a^p)⁰=a^p·0. Если же и p=0 и q=0, то (a⁰)⁰=1⁰=1 и a^0·0=a⁰=1, откуда (a⁰)⁰=a^0·0.

Теперь докажем, что (a^−p)^q=a^(−p)·q. По определению степени с целым отрицательным показателем 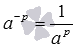, тогда 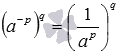. По свойству частного в степени имеем 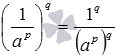. Так как 1^p=1·1·…·1=1 и 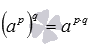, то 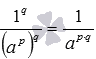. Последнее выражение по определению является степенью вида a^−(p·q), которую в силу правил умножения можно записать как a^(−p)·q.

Аналогично .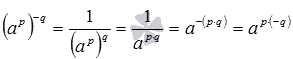

И .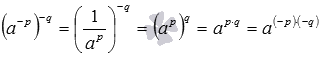

По такому же принципу можно доказать все остальные свойства степени с целым показателем, записанные в виде равенств.

В предпоследнем из записанных свойств стоит остановиться на доказательстве неравенства a⁻ⁿ>b⁻ⁿ, которое справедливо для любого целого отрицательного −n и любых положительных a и b, для которых выполняется условие a<b. Доказываемое неравенство по определению степени с целым отрицательным показателем можно переписать как 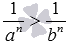. Запишем и преобразуем разность левой и правой частей этого неравенства: 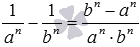. Так как по условию a<b, то по свойству степени с натуральным показателем aⁿ<bⁿ, следовательно, bⁿ−aⁿ>0. Произведение aⁿ·bⁿ тоже положительно как произведение положительных чисел aⁿ и bⁿ. Тогда полученная дробь 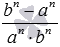положительна как частное положительных чисел bⁿ−aⁿ и aⁿ·bⁿ. Следовательно, 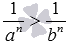откуда a⁻ⁿ>b⁻ⁿ, что и требовалось доказать.

Последнее свойство степеней с целыми показателями доказывается так же, как аналогичное свойство степеней с натуральными показателями.