В.В. Христич
1.1. Простейшая цепь общего вида
Здесь под простейшими линейными цепями понимаются электрические цепи со схемой рис. 1.1, где 
и 
– это или резисторы, или конденсаторы, или катушки индуктивности, или их несложные комбинации.
Контурный ток
,
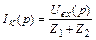протекающий под действием напряжения 
, создает на элементе падение напряжения
.
Отношение выходного напряжения цепи 
к входному при комплексном характере сопротивлений и является функцией передачи цепи
.
При анализе цепи в частотной области функцию передачи представляют в показательной форме:
.
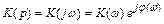Зависимость модуля 
от частоты называется амплитудно-частотной характеристикой (АЧХ), а зависимость аргумента 
от частоты – фазочастотной характеристикой (ФЧХ).
Выражения функций передачи, а также амплитудно-частотных и фазочастотных характеристик рассматриваемых здесь цепей можно найти из выражения 
базовой цепи, если для каждой из указанных цепей идентифицировать сопротивления и . При этом форма графиков АЧХ таких простых цепей легко объясняется характером зависимости сопротивлений реактивных элементов от частоты и свойствами параллельного и последовательного LC -контуров.
1.2. Интегрирующая RC -цепь 1-го порядка
Как следует из рис. 1.2, 
, 
, поэтому
; 
; 
.
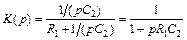Графики АЧХ и ФЧХ цепи рис. 1.2 приведены на рис. 1.9. Спад АЧХ в области верхних частот объясняется уменьшением сопротивления конденсатора 
с увеличением частоты 
и, как следствие, уменьшением напряжения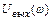 
.
1.3. Дифференцирующая RC -цепь 1-го порядка
В соответствии с рис. 1.3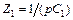 
, 
, а
; 
; 
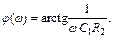
Графики АЧХ и ФЧХ цепи рис. 1.3 приведены на рис. 1.10. Спад АЧХ в области нижних частот вызван увеличением сопротивления конденсатора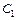 
при уменьшении частоты и, как следствие, уменьшением напряжения .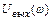
1.4. Дифференцирующая RL -цепь 1-го порядка
Как видно из рис. 1.4, , 
, следовательно
;
; 
.
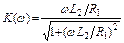Графики АЧХ и ФЧХ цепи рис. 1.4 приведены на рис. 1.10. Спад АЧХ в области нижних частот объясняется уменьшением сопротивления катушки индуктивности 
при уменьшении частоты и, как следствие, уменьшением напряжения .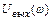
1.5. Интегрирующая RL -цепь 1-го порядка
В соответствии с рис. 1.5 
, , вследствие чего
;
; 
.
Графики АЧХ и ФЧХ цепи рис. 1.5 приведены на рис. 1.9. Спад АЧХ в области верхних частот вызван уменьшением напряжения 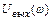при увеличении частоты из-за увеличения сопротивления катушки индуктивности 
.
1.6. RLC -цепи с параллельным LC -контуром
На рис. 1.6, а и б представлены RLC -цепи двух видов: с параллельным LC -контуром в поперечной и продольной ветвях (соответственно вместо и ).
Рис. 1.6. RLC -цепи с параллельным LC -контуром
В схеме рис. 1.6, а ; 
;
;
; 
.
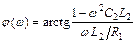В схеме рис. 1.6, б 
; ;
;
; 
.
Графики АЧХ и ФЧХ цепей рис. 1.6, а и б приведены соответственно на рис. 1.11 и 1.12. В схеме рис. 1.6, а выходное напряжение снимается с параллельного LC -контура, сопротивление которого (при идеальных элементах и ) на частоте параллельного резонанса 
стремится к бесконечности, поэтому коэффициент передачи цепи рис. 1.6, а на частоте 
равен единице (
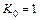). При отклонении частоты от сопротивление параллельного LC -контура уменьшается (уменьшается сопротивление элементов или ), что, как видно из рис. 1.11, приводит к спаду АЧХ как в области нижних, так и в области верхних частот.
В схеме рис. 1.6, б выходное напряжение снимается с резистора 
после параллельного LC -контура, поэтому на частоте параллельного резонанса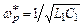 
, где сопротивление контура близко к бесконечности, коэффициент передачи равен нулю, т.е. реализуется нуль передачи на частоте (рис. 1.12). На этой же частоте, как видно из выражения и фазочастотной характеристики рис. 1.12, наблюдается скачок фазы от 
до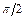 
.
1.7. RLC -цепи с последовательным LC -контуром
На рис. 1.7, а и б представлены RLC -цепи двух видов: с последовательным LC -контуром в поперечной и продольной ветвях (соответственно вместо и ).
Рис. 1.7. RLC -цепи с последовательным LC -контуром
В схеме рис. 1.7, а ; 
;
;
; 
.
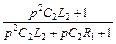В схеме рис. 1.7, б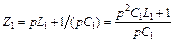 
; ;
;
; 
.
Графики АЧХ и ФЧХ цепей рис. 1.7, а и б приведены соответственно на рис. 1.12 и 1.11. В схеме рис. 1.7, а выходное напряжение снимается с последовательного LC -контура, сопротивление которого как на частотах 
, так и на частотах 
стремится к бесконечности, поэтому коэффициент передачи цепи рис. 1.7, а на этих частотах равен единице. На частоте последовательного резонанса 
сопротивление LC -контура (в случае элементов без потерь) равно нулю, нулевым будет и коэффициент передачи на частоте 
, что видно из графика амплитудно-частотной характеристики рис. 1.12.
В схеме рис. 1.7, б выходное напряжение снимается с резистора после последовательного LC -контура, вследствие чего АЧХ и ФЧХ (рис. 1.11) этой цепи будут такими же, как и соответствующие характеристики цепи рис. 1.6, а, где выходное напряжение снимается с параллельного LC -контура.
1.8. RLC -цепи с последовательно-параллельным LC -контуром
В схеме рис. RLC -цепи рис. 1.8, а выходное напряжение снимается с последовательно-параллельного LC -контура 
, а в схеме рис. 1.8, б – с резистора , включенного последовательно с LC -контура 
.
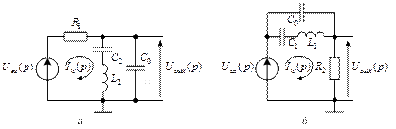
Рис. 1.8. RLC -цепи с последовательно-параллельным LC -контуром
Последовательно-параллельный LC -контур характеризуется двумя частотами резонанса – последовательного и параллельного, на которых такой LC -контур имеет соответственно нулевое и бесконечное сопротивления (при отсутствии потерь в элементах L и C).
Цепь рис. 1.8, а описывается следующими выражениями параметров и характеристик:
; 
;
;
;
.
Для цепи рис. 1.8, б эти же выражения имеют следующий вид:
; 
;
;
;
.
Поскольку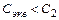 
и 
, частота параллельного резонанса LC -контура больше частоты последовательного резонанса (
), поэтому частота нуля передачи, как видно из рис. 1.13 и 1.14, цепи рис. 1.8, а лежит ниже частоты максимума, а цепи рис. 1.8, б – наоборот, выше.