Тема 8. ИНДЕКСЫ
Задача 8.1. Имеются данные о продаже товаров на одном из рынков города:
| Вид товара | Продано товаров, тыс. ед. | Цена единицы, руб. | ||
| апрель | май | апрель | май | |
| Товар А, кг | ||||
| Товар В, л | ||||
| Товар С, кг | ||||
| Итого |
Определите индивидуальные индексы по каждому товару.
Решение. Индивидуальный индекс цен равен 
, где 
и 
− цена продукции в базовом и отчетном периодах соответственно.
Индивидуальный индекс физического объема продаж равен 
, где 
и 
− физический объем продаж продукции в базовом и отчетном периодах соответственно.
Подставив соответствующие значения, получим следующую таблицу рассчитанных значений индивидуальных индексов:
| Вид товара | Продано товаров, тыс. ед. | Цена единицы товара, руб | Индивидуальные индексы, % | |||
| апрель,
| май,
| апрель,
| май,
| цен,
| физического объема продаж, 
| |
| Товар А, кг | ||||||
| Товар В, л | ||||||
| Товар С, кг | ||||||
| Итого |
Задача 8.2. Имеются следующие данные о реализации продукции в области
| Наименование товара | Июль | Август | ||
| цена за кг, руб. | продано тон | Цена за кг, руб. | Продано тон | |
| Товар А | ||||
| Товар В | ||||
| Товар С | ||||
| Итого |
Определите: 1) общий индекс товарооборота; 2) общий индекс физического объема товарооборота; 3) общий индекс цен; 4) прирост товарооборота - всего, в том числе за счет изменения цен и объема продажи товаров; 5) покажите взаимосвязь между исчисленными индексами.
Решение. Составим вспомогательную расчётную таблицу.
| Наиме- нование товара | Июль | Август | Расчетные величины, руб. | ||||
| цена за кг, руб.,
| продано тон,
| Цена за кг, руб.,
| Продано тон,
| 
| 
| 
| |
| Товар А | |||||||
| Товар В | |||||||
| Товар С | |||||||
| Итого |
Здесь – стоимость продукции базисного периода по ценам того же периода; – стоимость продукции отчетного периода по ценам базисного; – стоимость продукции отчётного периода по ценам того же периода.
1) Общий индекс товарооборота исчисляется по формуле:
или ______%.
Таким образом, по сравнению с июлем товарооборот в августе снизился/повысился (ненужно зачеркнуть) на _______%.
2) Общий индекс физического объема товарооборота (количества проданных товаров) исчисляется по формуле:
или ______%.
Это значит, что количество проданного товара в августе было больше/меньше (ненужное зачеркнуть) на _______%, чем в июле.
3) Общий индекс цен равен:
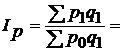
или ______%.
Т.е. цены на все товары в среднем снизились/повысились (ненужное зачеркнуть) на ________%.
4) Прирост или снижение товарооборота исчисляется как разница между числителем и знаменателем индекса товарооборота:
Это снижение/повышение (ненужное зачеркнуть) обусловлено изменением цен на товары и изменением количества проданных товаров.
Снижение/прирост за счет изменения цен составил:
Снижение/прирост за счет изменения количества проданных товаров:
Следовательно, снижение/повышение товарооборота на ______ тыс. руб. произошло за счет повышения/понижения количества проданных товаров на ________ тыс. руб. и за счет снижения цен на ______ тыс. руб. (ненужное зачеркнуть).
5) Между исчисленными индексами существует связь: 
.
Используя взаимосвязь индексов, проверим правильность вычислений:
_____________________________________
Задача 8.3. Имеются следующие данные о количестве произведенной продукции и ее себестоимости
| Продукция | Количество произведенной продукции, тыс. шт. | Себестоимость единицы продукции, руб. | ||
| А | ||||
| Б | ||||
| В | ||||
| Итого |
Вычислить: 1) общий индекс затрат на продукцию; 2) общий индекс физического объема продукции; 3) общий индекс себестоимости; 4) экономический эффект от снижения себестоимости.
Решение. Составим вспомогательную расчётную таблицу.
| Продукция | Количество произведенной продукции, тыс. шт. | Себестоимость единицы продукции, руб. | Расчетные величины, руб. | ||||
|
|
|
|
| 
| 
| 
| |
| А | |||||||
| Б | |||||||
| В | |||||||
| Итого |
1) Общий индекс затрат на производство продукции можно рассчитать, как
или ______%.
Это говорит о том, что ___________________________________________________
__________________________________________________________________________________________________________________________________________________________
2) Общий индекс физического объема продукции:
или ______%.
Это говорит о том, что ___________________________________________________
__________________________________________________________________________________________________________________________________________________________
3) Общий индекс себестоимости вычисляется, как
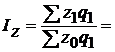
или ______%.
Это говорит о том, что ___________________________________________________
__________________________________________________________________________________________________________________________________________________________
Проверяем связь между индексами: 
.
_________________________________________
4) Экономический эффект от снижения себестоимости.
Абсолютное изменение затрат в отчетном году по сравнению с базисным:
В том числе за счет изменения себестоимости единицы продукции
За счет изменения физического объема производства
В отчетном периоде по сравнению с базисным затраты на производство выросли/упали на _________ тыс. руб. или на _______%, в том числе за счет изменения физического объема производства выросли/упали _________ тыс. руб. или на _________%, за счет изменения себестоимости снизились/повысились на _________ тыс. руб. или на ________%.
Задача 8.4. Имеются следующие данные по росту производительности труда на предприятии.
| Вид продукции | Затраты времени на 1 изделие, чел.-ч. | Произведено, штук | ||
| Январь | Февраль | Январь | Февраль | |
| Изделие А | ||||
| Изделие В | ||||
| Изделие С | ||||
| Итого |
Рассчитать агрегатный индекс производительности труда по трудоемкости. 2) Оценить изменение затрат труда в результате изменения производительности труда.
Решение. Составим вспомогательную расчётную таблицу.
| Вид продукции | Затраты времени на 1 изделие, чел.-ч. | Произведено, штук | Расчетные величины, руб. | |||
Январь 
| Февраль 
| Январь
| Февраль
| 
| 
| |
| Изделие А | ||||||
| Изделие В | ||||||
| Изделие С | ||||||
| Итого |
1) Агрегатный индекс производительности труда по трудоёмкости вычисляется по формуле:
или ______%.
Это значит, что прирост/снижение (ненужное зачеркнуть) производительности труда в целом по предприятию составил _____%.
2) Затраты труда на производство продукции отчетного периода, взвешенной по трудоемкости базисного периода представляют собой сумму 
. Затраты труда на производство продукции в отчетном периоде - 
. Тогда разность между двумя этими величинами характеризует изменение затрат труда в результате изменения производительности труда:
Задача 8.5. Имеются следующие данные о производстве продукции и отпускных
ценах предприятия.
| Вид продукции | Сентябрь | Октябрь | Отпускная цена, руб. | ||
| произведено, шт. | трудовые затраты, чел.-ч | произведено, шт. | трудовые затраты, чел.-ч | ||
| Изделие А | |||||
| Изделие В | |||||
| Изделие С | |||||
| Итого |
Вычислить: 1) индекс производительности труда в стоимостном выражении (по выработке); 2) индекс затрат рабочего времени; 3) индекс физического объема продукции, взвешенный по отпускной цене.
Решение. Составим вспомогательную расчётную таблицу.
| Вид продукции | Сентябрь | Октябрь | Отпускная цена, руб. p | Расчетные величины, руб. | |||
| произведено, шт.
| трудовые затраты, чел.-ч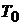 
| произведено, шт.
| трудовые затраты, чел.-ч 
| 
| 
| ||
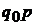
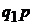
| Изделие А | |||||||
| Изделие В | |||||||
| Изделие С | |||||||
| Итого |
1) Сводный индекс производительности труда в стоимостном выражении (по выработке) вычисляется по формуле:
или ______%.
Таким образом, в текущем периоде за 1 человеко-час вырабатывалось 
______ руб. продукции, а в базисном – 
________ руб. Снижение/рост производительности труда составило _______%.
2) Индекс затрат рабочего времени рассчитывается, как
или ______%.
3) Индекс физического объема продукции, взвешенный по отпускной цене можно вычислить, как произведение индекса производительности труда по выработке на индекс затрат рабочего времени:
или ______%.
Задача 8.6. Имеются следующие данные о реализации продукции в области
| Товар | Реализация в текущем периоде, руб. | Изменение цен в текущем периоде по сравнению с базисным, %, 
|
| Товар А | ||
| Товар В | ||
| Товар С | ||
| Итого | - |
Вычислить агрегатный индекс цен.
Решение. Составим вспомогательную расчётную таблицу.
| Товар | Реализация в текущем периоде, руб., 
| Изменение цен в тек. периоде по сравнению с базисным, %,
| Расчетные величины | |
| 
| |||
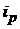
| Товар А | ||||
| Товар В | ||||
| Товар С | ||||
| Итого | - | - |
Агрегатный индекс цен вычисляется по формуле средней гармонической:
или ______%.
Задача 8.7. Имеются следующие данные о реализации продукции в натуральном и стоимостном выражениях
| Товар | Реализация в базисном периоде, руб. | Изменение физического объема реализации в текущем периоде по сравнению с базисным, %,
|
| Товар А | ||
| Товар В | ||
| Товар С | ||
| Итого | - |
Найти индекс физического объема товарооборота.
Решение. Составим вспомогательную расчётную таблицу.
| Товар | Реализация в базисном периоде, руб., 
| Изменение физ. объема реализации в тек. периоде по сравнению с базисным, %,
| Расчетные величины | |
| 
| |||
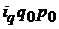
| Товар А | ||||
| Товар В | ||||
| Товар С | ||||
| Итого | - | - |
Физический объем товарооборота вычисляется по формуле средней арифметической:
или ______%.
Задача 8.8. Имеются данные об объеме производства и себестоимости 1 тонны бумаги по трём филиалам предприятия за 2 смежных периода:
| Филиал | Произведено (тонн) | Себестоимость 1 т (т.руб) | ||
| в базисном периоде | в отчетном периоде | в базисном периоде | в отчетном периоде | |
| Итого |
Найти индексы: 1)средней себестоимости 1 тонны бумаги (индекс переменного состава); 2) индекс постоянного состава; 3) индекс структурных сдвигов. Объясните полученные результаты.
Решение. Составим вспомогательную расчётную таблицу.
| Филиал | Произведено (тонн) | Себестоимость 1 т (т.руб) | Расчетные величины | ||||
| в базисном
периоде,
| в отчетном
периоде,
| в базисном периоде, 
| в отчетном периоде, 
| 
|
| 
| |
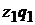
| Итого |
1) Индекс переменного состава характеризует совместное влияние сразу двух факторов (изменения себестоимости и объема производства продукции на каждом филиале) на изменение среднего уровня себестоимости 
продукции предприятия:
или ______%.
Значит, под влиянием 2-х факторов себестоимость 1 тонны бумаги по предприятию (3-м филиалам) снизилась/повысилась на 100% – _____%= ______ %.
2) Индекс постоянного состава характеризует влияние изменений только уровней самого признака z при неизменной (фиксированной) структуре совокупности (долях выпуска филиалов в общем выпуске продукции предприятия). Как правило, структуру совокупности фиксируют на уровне текущего (отчетного) периода:
или ______%.
Значит, себестоимость 1 тонны бумаги на предприятии снизилась/повысилась на ________ за счет влияния одного фактора – изменения себестоимости на каждом филиале.
3) Индекс структурных сдвигов характеризует влияние изменения другого фактора – структуры изучаемого явления (долей филиалов в производстве продукции предприятия) на изменение средней себестоимости. Уровни самого признака – себестоимости – в данном индексе фиксируются по базисному периоду:
или ______%.
Средняя себестоимость 1 тонны бумаги снизилась/повысилась на _____% за счет изменения удельного веса (долей) филиалов в выпуске продукции.
Между тремя рассмотренными индексами должна существовать следующая взаимосвязь:
.
Проверяем:
______________________________
Вывод: _________________________________________________________
___________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Задача 8.9. Имеются следующие данные о продаже картофеля на рынках города за два месяца:
| Рынок | Февраль | Март | ||
| кол-во, т | средняя цена 1 кг, руб. | кол-во, т | средняя цена 1 кг, руб. | |
На основе приведенных данных определить: 1) динамику средней цены на картофель (индекс переменного состава); 2) среднее изменение цены на картофель (индекс постоянного состава); 3) влияние изменения структуры продажи картофеля на динамику средней цены (индекс структурных сдвигов). Объясните полученные результаты.
Решение. Составляем вспомогательную расчётную таблицу
| Рынок | Февраль | Март | Расчётные величины | ||||
| кол-во, т
| средняя цена
1 кг, руб.
| кол-во, т
| средняя цена 1 кг, руб.
| 
|
| 
| |
1. В данном случае индекс переменного состава характеризует динамику изменения средней цены на картофель под влиянием двух факторов: изменения цены на картофель и изменения объёма продаж. Вычислить его можно по следующее формуле:
или ______%.
2. Индекс постоянного состава характеризует изменение средней цены на картофель при неизменном уровне объёма продаж и вычисляется, как:
или ______%.
3. Индекс влияния структурных сдвигов, показывает влияние изменения структуры (объёма) продажи картофеля на динамику средней цены. Уровни самого признака – цены – в данном индексе фиксируются по базисному периоду:
или ______%.
4. Проверим правильность произведенных расчетов через взаимосвязь между индексами:
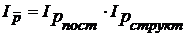
или
________________________________________________
Вывод: Средняя цена на картофель по всем рынкам города в марте месяце по сравнению с февралем увеличилась/уменьшилась на ________ %. На величину этого индекса оказали влияние два фактора: изменение самой цены и изменение в объёме продаж. За счет динамики цены на картофель средняя цена на картофель по всем рынкам города выросла/упала на _______ %. За счет изменения объёма продаж средняя цена на картофель по всем рынкам города выросла/упала на ______ %. (ненужное зачеркнуть)
Задача 8.10. Имеются данные об объеме продаж и ценах на 2 вида продукции:
| Продукция | ||||||
| Объем (шт.) | Цена (руб) | Объем (шт.) | Цена (руб) | Объем (шт.) | Цена (руб) | |
| А | ||||||
| Б |
Найти 1) базисные индексы физического объема продукции с постоянными весами (в ценах 2000 г); 2) цепные физического объема с постоянными весами; 3) базисные индексы цен с переменными весами; 4) цепные индексы цен с переменными весами.
Решение. 1) Найдем базисные индексы физического объема продукции с постоянными весами (в ценах 2000 г):
или ______%.
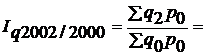или ______%.
2) Вычислим цепные физического объема с постоянными весами:
или ______%.
или ______%.
3) Найдем базисные индексы цен с переменными весами:
или ______%.
или ______%.
4) Найдем цепные индексы цен с переменными весами:
или ______%.
или ______%.
Для цепных индексов с постоянными весами (индексов физического объема) существует правило: произведение цепных индексов равно базисному индексу для последнего периода.
.
Проверяем верность этого утверждения:
_______________________________________________________________
Для индексов цен (индексов с переменными весами) такая взаимосвязь отсутствует.
Приложение
Индексируемые (изменяемые) величины в индексном методе обозначаются следующими символами:
q – количество (объем) продукта в натуральном выражении;
р – цена единицы продукта;
z – себестоимость единицы продукта;
f – заработная плата работника;
t – трудоёмкость (затраты рабочего времени на производство единицы продукции);
w = 1/t – производительность труда (количество продукции, произведённой за единицу времени);
T – суммарные затраты времени на выпуск данной продукции в человеко-часах, человеко-днях, или человеко-месяцах;
qp – стоимость продукции данного вида (товарооборот, выручка);
zq – затраты (издержки) на производство продукции данного вида.
Чтобы отличать, к какому из сравниваемых периодов относятся индексируемые величины, возле символа величины внизу справа ставят подстрочный знак: 1 – для сравниваемого (текущего, отчетного) периода, 0 – для периода, с которым производится сравнение (предыдущего, базисного).
Индивидуальные индексы обозначаются символом i и добавляются подстрочным символом индексируемой величины. Например, 
– индивидуальный индекс цен.
Общие индексы обозначаются символом I и добавляются подстрочным символом индексируемой величины. Например, 
– общий индекс цен.
Индивидуальные индексы
| Индивидуальный индекс цен |
| ||
| Индивидуальный индекс физического объема продаж |
| ||
| Индивидуальный индекс себестоимости | 
| ||
| Индивидуальный индекс трудоёмкости | 
| 
| 
|
| Индивидуальный индекс производительности труда | 
| 
| 
|
| Индивидуальный индекс товарооборота (отражает изменение объема реализации товара в стоимостном выражении) | 
|
Общие агрегатные индексы
| Наименование индекса | Формула | Примечание |
| Общий индекс товарооборота | 
| характеризует изменение стоимости совокупности проданных товаров в среднем в одном периоде по сравнению с другим |
| Общий индекс физического объема товарооборота (продукции) | 
| характеризует влияние изменения объема продажи товаров на динамику товарооборота (во сколько раз изменилась стоимость продукции в результате изменения объема ее производства) |
по формуле средней арифметической
| ||
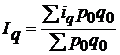
| Общий индекс (отпускных) цен | 
| отражает влияние изменения цен на динамику товарооборота, т. е. показывает, во сколько раз изменилась стоимость продукции в результате изменения цен |
по формуле средней гармонической
| ||
| Связь между индексами |
| |
| Общий индекс себестоимости продукции |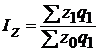 
| характеризует динамику (изменение) себестоимости всех видов разнородной продукции |
| Общий индекс физического объёма продукции | 
| показывает, во сколько раз возросла (уменьшилась) стоимость продукции из-за роста (снижения) объёма производства |
| Общий индекс затрат на производство (издержек производства) |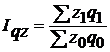 
| характеризует общее изменение затрат на производство отдельных видов продукции |
| Связь между индексами |
| |
| Общий индекс затрат рабочего времени | 
| показывает, во сколько раз изменились затраты времени на производство продукции |
| Общий индекс физического объема продукции (по трудоемкости) |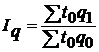 
| показывает, во сколько раз изменились затраты времени на производство продукции в результате изменения объема ее производства |
| Общий индекс производительности труда по трудоёмкости | 
| показывает, во сколько раз изменились затраты времени на производство продукции в результате изменения ее трудоемкости |
| Связь между индексами | 
|
Индексы средних величин
| Индекс переменного состава | 
|
| Индекс постоянного состава | 
|
| Индекс структурных сдвигов | 
|
| Связь между индексами | 
|
Здесь 
уровни осредняемого показателя в базисном и отчетном периодах соответственно;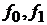 
веса (частоты) осредняемого показателя (уровни количественного показателя) в базисном и отчетном периодах соответственно.
Абсолютные величины
| Абсолютное увеличение товарооборота в отчетном периоде по сравнению с базисным | 
|
| Абсолютная фактическая экономия от снижения цен в отчетном периоде | 
|
| Абсолютная условная экономия в базовом периоде | 
|
| Абсолютное изменение физического объема | 
|
| Взаимосвязь абсолютных показателей |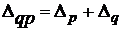 
|
| Абсолютное изменение затрат в отчетном году по сравнению с базисным | 
|
| Абсолютное изменение затрат в отчетном году за счет изменения себестоимости единицы продукции | 
|
| Абсолютное изменение затрат в отчетном году за счет изменения физического объема производства | 
|
| Взаимосвязь абсолютных показателей | 
|
| Изменение затрат труда в результате изменения производительности труда | 
|