1. Напряжение, которое приложено к пластинам конденсатора: U=E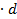 
U=375 
56,25 B
2. Основной характеристикой конденсатора является его емкость, под которой принимают величину, пропорциональную заряду Q и обратно пропорциональную разности потенциалов между обкладками:
С = 
, отсюда заряд обкладки конденсатора Q = CU
Q = 20 
= 1,125 
Кл
3. 
, 
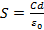, учетом того что пластика конденсатора обладает квадратной формой, имеем: 
, следовательно 
Вывод графических зависимостей
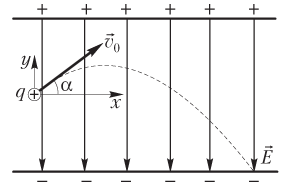
Траекторией движения частицы под действием кулоновской силы внутри конденсатора (сила тяжести в этой ситуации пренебрежимо мала) является участок параболы.
Рис.3 Траектория движения частицы
Проекции скорости частицы на координатные оси:
на горизонтальную ось:
x = 0 cos α = const, где 0 — модуль начальной скорости частицы; α — угол, который составляет вектор начальной скорости частицы с горизонтом;
вертикальную ось:
y = 0 sin α − at, где a — модуль ускорения, вызванного кулоновской силой F кул:
из второго закона Ньютона F = ma
a = Fкул/m = qE/m, где m — масса заряженной частицы; q — величина заряда частицы; E — модуль напряженности поля конденсатора;
Величина скорости заряженной частицы в произвольный момент времени t определяется по формуле:
= 
= 
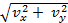Изменения координат заряженной частицы за промежуток времени ∆t = t от начала движения определяются следующим образом:
по горизонтальной оси:
∆x = L = v 0t cos α, (1) где ∆x — смещение частицы по горизонтали;
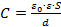; т.к. пластины конденсатора квадратные, то можно заменить S= 
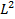. Значит
по вертикальной оси:
Δy=∣v0t sinα − at2/2∣=∣v0t sinα − qEt2/2m∣,
где ∆y — смещение частицы по вертикали.
Найдем время полета частицы в конденсаторе из (1)
t =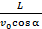 
t = 
= 3,856 
с
Проверка вылета электрона за пределы конденсатора:
Δy=∣v0t sinα − at2/2∣=∣v0t sinα − qEt2/2m∣,
Δy = |v0t sinα − qEt2/2m∣
Δy = 
- 
Δy = 
= 0,117 (м)
y0 + Δy = 0,006 + 0,117 = 0,123 
0,15 м - электрон выйдет за пределы конденсатора.
Найдем скорость, с которой электрон вылетает из конденсатора
=
1,546 
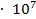(м/с)
Электрон при вылете из конденсатора влетает в магнитное поле.
Рис.4 Магнитное поле, образованное вокруг конденсатора
На заряженную частицу со стороны магнитного поля действует сила Лоренца
= q[ 
],
здесь q – заряд частицы, В – магнитная индукция, v – скорость заряженной частицы. Направление силы Лоренца определяется по правилу левой руки.
Если скорость заряженной частицы направлена под углом α к вектору В, то ее движение можно представить в виде суперпозиции:
1) равномерного прямолинейного движения вдоль поля со скоростью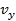 
= const;
2)равномерного движения со скоростью 
по окружности в плоскости, перпендикулярной полю под действием силы Лоренца.
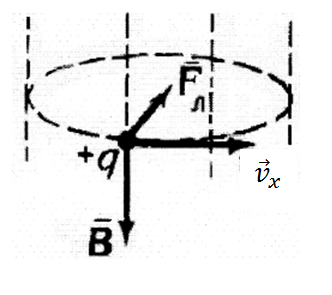
Рис.5 Направление силы Лоренца
Нормальное ускорение частицы и скорость частицы внутри конденсатора внутри найдем следующим образом:
, где 
изменение модуля скорости; 
изменение кривизны траектории;
= 
; 
= 
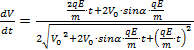
Получаем следующие зависимости:
= 
= 
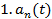посторить график
Полное ускорение частицы: 
. Подставим 
, 
Подставить циферки и будет график
Графики зависимостей 
(t) и V(x)
Рис.6 Зависимость V от x
Вывод
В расчетно-графическом задании рассматривалось движение позитрона в однородном электрическом поле между обкладками заряженного конденсатора. Для выполнения задания было исследовано устройство и основные характеристиками конденсатора, также рассмотрено движение заряженной частицы в однородном электрическом поле. Рассчитаны недостающие параметры: 
. Построенные графики отображают зависимости: 
(t) – нормальной составляющей ускорения от времени; V(x) – скорости частицы внутри конденсатора от времени.