Цель работы: расчетное и экспериментальное определение критических сил стержней большой и средней гибкости; сравнение результатов расчета и эксперимента.
Формы равновесия элементов конструкций (сжатых стержней, высоких винтовых пружин при сжатии, цилиндрических тонкостенных оболочек при растяжении и кручении, балок-стенок при изгибе, оболочек при внешнем давлении и др.) могут быть устойчивыми и неустойчивыми. Если нагруженная упругая система (элемент конструкции), выведенная из первоначального положения равновесия небольшой дополнительной силой, возвращается в исходное положение после удаления дополнительной силы, то такая форма равновесия упругой системы называется устойчивой, а если не возвращается в исходное положение, - неустойчивой формой равновесия. Нагрузки и напряжения, которые характеризуют переход упругой системы из устойчивой к неустойчивой форме равновесия, называются критическими. Потеря устойчивости применительно к центрально сжатому стержню называется продольным изгибом.
Определение критической силы стержня большой гибкости
Постановка опыта. Стержень (l = 144 мм; bх h = 2,5 х 34 мм2; µ = 1) из углеродистой стали (Е = 2 ∙ 105 МПа; δпц = 158 МПа; δт = 197 МПа) подвергается продольному изгибу на лабораторной установке. При критическом значении силы Pэкр показания динамометра пкр, = 121 дел. Цена деления динамометра к = 34 Н/дел.
Требуется: определить Ркр, δкр; Pэкр,δкр э, отклонение результатов расчета от эксперимента 
1. Вычисляем гибкость, соответствующую пределу пропорциональности δпц= 158 МПа;
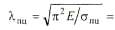
=112
2. Находим гибкость испытуемого стержня прямоугольного сечения:
=0,722мм; 
|
|
Схема лабораторной установки для испытаний на устойчивость стержня большой гибкости
3. Определяем расчетные значения критической силы и критического напряжения. Поскольку гибкость стержня X = 199 > Хпи = 112, то используем формулы Л. Эйлера:
= 3,142 *2*105/1992 =49,8МПа
4.Вычесляем критические напряжения для ряда гибкостей:
5. Экспериментальные значения критической силы и критического напряжения равны:
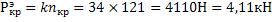
6. Отклонение результатов расчета от эксперимента
Определение критической силы стержня средней гибкости
Постановка опыта. Стержень (l = 220 мм; d = 10 мм; µ = 1) из той же (п. 13.3.1) углеродистой стали (а = 264 МПа; b = 0,951 МПа) подвергается продольному изгибу в специальном приспособлении (рис.) на машине УГ-20. По показаниям силоизмерителя экспериментальное значение критической силы. 
= 13,9 кН.
Требуется: определить Ркр, σкр, 
; 
Построить диаграмму критических напряжений σкр-λ для 0 < λ < 2λпц; нанести на нее результаты опытов (п. 13.3.1 и 13.3.2); сделать выводы о соответствии результатов расчета и эксперимента.
Схема приспособления для испытаний на устойчивость стержня средней гибкости
1. Вычисляем гибкость, соответствующую пределу текучести σт= 197 МПа:
= (264 - 197)/0,951 = 70,5.
2. Находим гибкость испытываемого стержня круглого сечения d= 10 мм:
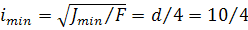= 2,50 мм; λ = 1 • 220/2,50 = 88,0.
3. Определяем расчетные значения критической силы и критического напряжения. Поскольку гибкость стержня λt = 70,5 < λ = 88 < λпц = 112, то применяем формулы Ф. С. Ясинского:
Ркр = (а - bl)F = (264 -0,951*88)-3,14*102 • 10-6/4 = 14 100 Н = 14,1 кН;
|
|
σкр= (a-bλ)F = 264-0,951*88 = 180 МПа >σпц= 158 МПа.
4. Вычисляем экспериментальное значение критического напряжения при 
=13,9кН:
= 
= 13900/(3,14 * 102 • 10-6/4)= 177 МПа.
|
С учетом σт = 197 МПа и λt = 70,5, σпц = 158 МПа и λ.пц = 112 и полученных в п. 4 значений σкр строим диаграмму критических напряжений σкр - λ (рис. 13.6). Наносим на нее результаты опытов (экспериментальные значения
Диаграмма критических напряжений для заданной углеродистой стали
5. Отклонение результатов расчета от эксперимента
= 100(14,1 -13,9)/13,9 = 1,4 %.
Выводы:
1. Отклонение результатов расчетов от экспериментов составляет в данных опытах 2,4 и 1,4 %, что подтверждает приемлемость для практики формул Л. Эйлера и Ф. С. Ясинского для расчетов на устойчивость элементов конструкций.
2.Расхождения между расчетными и экспериментальными значениями критических сил обусловлены принятыми гипотезами при выводе формул, а также погрешностями опытов при определении критических сил.