Определение длин волн линий ртути.

Упражнение 1.

Определение радиуса кривизны линзы.

Измерения:

1) Зажигают ртутную лампу, поместив у окна защитного кожуха светофильтр, выделяющий зеленую линию ртути (λ = 5460 Ǻ, 1 Ǻ = 1 ангстрем = 10^-10 м).

2) Сняв линзу, фокусируют микроскоп на верхнюю поверхность черного стекла, положив на него кусок миллиметровой бумаги. Поставив затем линзу в прежнее положение, устанавливают черную пластинку так, чтобы точка соприкосновения линзы и пластинки попала точно в центр поля зрения микроскопа. При этом образующиеся на границе воздушного слоя и линзы ньютоновы кольца должны быть отчетливо видны. Если этого не будет, то, не снимая линзы, исправляют фокусировку микроскопа. Если в точке соприкосновения вместо темного кольца получится светлое, то это значит, что между поверхностями линзы и стекла имеются пылинки; последние следует удалить при помощи замши[1].

3) Вращая барабан окулярного микрометра, устанавливают его крест на середину ширины линии какого-нибудь достаточно удаленного от центра темного кольца, например, 20-го вправо, и производят отсчет по шкале и барабану окулярного микрометра. Смещая положение креста микрометра, повторяют измерение одного и того же кольца несколько раз и находят среднее значение. После этого, вращая барабан окулярного микрометра, наводят крест последовательно на 19-е, 18-е, 17-е и т.д. кольца и производят такие же отсчеты в том же направлении, т.е. вправо от центрального пятна, доходя до того же 20-го кольца. Проделывают такие же измерения со светлыми кольцами.

Если в поле зрения не видно полностью двадцать колец, то сначала измеряют диаметр центрального пятна, затем сдвигают столик с линзой так, чтобы был виден край центрального пятна, и начинают вправо или влево от него снимать отсчёты для двадцати тёмных колец. По полученным данным считают радиусы, которые и подставляют в формулы.

Так как ближайшие к центральному пятну несколько колец обычно бывают сильно размыты, что затрудняет установку на них креста, то их измерения можно не производить.

Вычисления:

Из полученных отсчетов определяют диаметры, а затем и радиусы колец, по формуле (7) определяют радиус кривизны линзы.

При этом в целях повышения точности результатов рекомендуется комбинировать радиус кольца номер k (четного) с радиусом кольца номер , кольца (нечетного) – с , и т.д. (20-е с 10-м, 19-е с 9-м и т.д.). Из полученных значений R берут среднее арифметическое. Здесь k – общее количество колец.

Упражнение 2.

Определение длин волн линий ртути.

1. В окно защитного колпака лампы вставляют светофильтр, выделяющий жёлтую или фиолетовую линию ртути; повторяют все измерения, указанные в упражнении 1.

2. Подставляя в формулу (7) значение радиуса кривизны линзы R, найденное в первом упражнении, определяют длину волны выделенной ртутной линии.

3. Можно определить длину волны линии ртути графическим методом.

Составив таблицу:

строят график, откладывая по оси ординат квадраты диаметров, а по оси абсцисс – номера колец. График должен быть прямой линией.

Длина волны λ определяется по тангенсу угла наклона прямой к оси абсцисс:

,

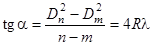(8)

где R – радиус кривизны линзы.

Если известна длина волны, то таким же образом находится радиус кривизны линзы.

Литература.

1. Г.С.Ландсберг, Оптика, Гостехиздат, 1957.

2. С.Э.Фриш и А.В.Тиморева, Курс общей физики, т. III, Физматгиз, 1962.

3. Р.Вуд, Физическая оптика, ОНТИ, 1936.

4. М.Ф.Романова, Интерференция света и её применение, ОНТИ, 1937.

5. А.Н.Захарьевский, Интерферометры, Оборонгиз, 1962.

6. Р.Дитчберн, Физическая оптика, "Наука", 1962, гл.5.

Контрольные вопросы.

1. Каковы условия когерентности различных источников колебаний?

2. Как можно реализовать условие когерентности для световых пучков? Что такое пространственная когерентность световых пучков (источников света)? Что такое когерентность во времени? Как реализуются пространственно когерентные световые пучки? Как можно на опыте проверить пространственную когерентность пучка?

3. Почему обычные источники света некогерентны между собой? Как можно реализовать частично когерентные источники света?

4. В каких случаях результирующая освещенность объекта несколькими световыми пучками равна сумме освещенностей, создаваемых каждым пучком в отдельности?

5. В чём содержание принципов суперпозиции амплитуд и суперпозиции интенсивностей? В каких случаях на опыте выполняется тот или иной принцип?

6. Какие простейшие оптические опыты позволяют наблюдать явление интерференции света?

7. Как можно получить и зарегистрировать стоячие световые волны?

8. В чем заключается интерференционный опыт по схеме Юнга?

9. Как реализуются интерференционные опыты с бипризмой, бизеркалами?

[1] Эта часть не выполняется, так как обычно всё настроено.