Курс 1 2 семестр
ЗАДАНИЕ
Вариант № 2
Инструкция
На выполнение письменной экзаменационной работы по математике дается 3 астрономических часа (180 минут).
Экзаменационная работа состоит из 2-х частей: обязательной и дополнительной. Обязательная часть содержит задания минимального обязательного уровня, а дополнительная часть – более сложные задания.
При выполнении большинства заданий обязательной части требуется представить ход решения и указать полученный ответ, и только в нескольких заданиях достаточно представить ответ.
При выполнении любого задания дополнительной части описывается ход решения и дается ответ.
Правильное выполнение заданий оценивается баллами.
Правильное выполнение любого задания обязательной части оценивается 1 балом, правильное выполнение каждого задания дополнительной части – тремя баллами. Баллы указываются в скобках около номера задания.
Если приводится неверный ответ или ответ отсутствует, ставится 0 баллов.
Баллы, полученные за все выполненные задания, суммируются.
Постарайтесь правильно выполнить как можно больше заданий и набрать как можно больше баллов.
Перед началом работы внимательно изучите критерии оценивания и обратите внимание, что начинать работу следует с заданий обязательной части. И только после того, как Вы наберете необходимое количество баллов для удовлетворительной оценки, можете переходить к заданиям дополнительной части, чтобы повысить оценку до четырех или пяти.
Обязательная часть
Задание №1. При выполнении заданий 1-8 запишите ход решения и полученный ответ.
1.(1 балл) В туристический поход на 7 дней отправляется группа из 8 человек. В походе на одного человека приходится 90 грамм сахара в день. Сколько трехкилограммовых мешков сахара нужно купить, чтобы сахара хватило на весь поход?
2.(1 балл) На графике показан процесс разогрева двигателя легкового автомобиля. На оси абсцисс откладывается время в минутах, прошедшее от запуска двигателя, на оси ординат – температура двигателя в градусах Цельсия. Определите по графику, сколько минут двигатель нагревался до температуры 600С.
3.(1 балл) Вычислите следующие пределы:
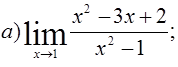
4.(1 балл) Вычислите значение выражения: 
∙ 
∙ 
.
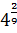5.(1 балл) Найдите значение sinα, если известно, что cosα = - 
, π 
6.(1 балл) Решите уравнение: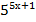 
= 252х
7.(1 балл) Вычислите значение выражения: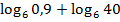 
8. (1 балл) Решите уравнение: 
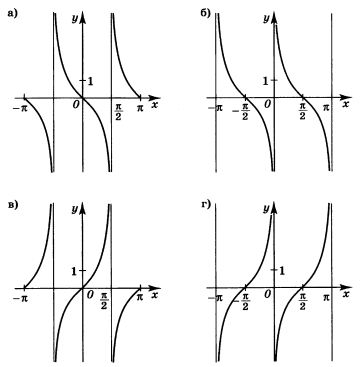
9. (1 балл)Определите, на каком из рисунков изображен график функции 
на промежутке 
Ответ запишите буквой.
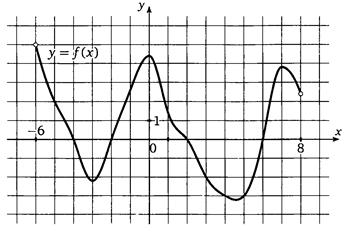
Задание №2. Используя график функции y=f(x) (см.рис. ниже), определите и запишите ответ:
10.(1 балл) наименьшее и наибольшее значения функции;
11.(1 балл) промежутки возрастания и убывания функции;
12.(1 балл) количество точек, в которых производная функции y=f(x) равна 0.
Задание №3. При выполнении заданий 13-18 запишите ход решения и полученный ответ.
13.(1 балл) Найдите производную функции: у= 2 cosx - 4 
14.(1 балл) Прямолинейное движение точки описывается законом S(t) = t4 – 2t2(м). Найдите её скорость в момент времени t = 3 с.
15.(1 балл) Вычислите интеграл: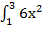 
dx=
16.(1 балл) Решите уравнение: 
= 7
17.(1 балл) Решите уравнение: sint = -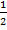 
18.Прямоугольник, диагональ которого равна 18 см и наклонена к основанию под углом 300, является осевым сечением цилиндра. Найдите площадь полной поверхности цилиндра.
Дополнительная часть
Задание №4. При выполнении заданий 19-22 запишите ход решения и полученный ответ.
19.(3 балла) Исследуйте функцию у = х3- 3х2 + 4 на монотонность и экстремумы.
20. (3 балла) Высота правильной четырехугольной призмы равна 2 см, а площадь боковой грани равна 16 см2. Найдите объем призмы.
21. (3 балла) Найдите производную функции: у = (8х – 15)8.
22. (3 балла) Найдите решение уравнения: 2sin2t + 3sint – 2 =0.
Критерии оценки:
| Оценка | Число баллов, необходимое для получения оценки |
| «3» (удовлетворительно) | 9 – 14 |
| «4» (хорошо) | 15 – 20 (не менее одного задания из дополнительной части) |
| «5» (отлично) | 21 – 30 (не менее двух заданий из дополнительной части) |
ПРОБНЫЙ ЭКЗАМЕН