Найдем параметры уравнения линейной регрессии и дадим экономическую интерпретацию коэффициента регрессии.
y расч = a0 +a1*x – уравнение линейной регрессии.
Возьмем данные из таблицы a0= 12,24, a1= 0,91.
Следовательно, уравнение регрессии имеет вид:
y расч = 12,24 + 0,91*x.
Если объем капиталовложений увеличится на 1 у.е., то объем выпуска продукции в среднем увеличится на 0,91 у.е. Таким образом наблюдается положительная корреляция признаков, что свидетельствует об эффективности работы предприятия и выгодности капиталовложений в их деятельности.
2. Вычислим остатки: данные взяли из ранее полученных таблиц.
Возведем остатки в квадрат через функцию «Степень» и найдем их сумму, через формулу 
График построили.
Проверить выполнение предпосылок МНК
Математическое ожидание случайной величины, как видно из табл. 2, равно нулю: 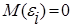 .
.
Случайный характер остатков (критерий поворотных точек, критерий пиков):
 ,
,
где n- количество наблюдений;
m – количество поворотных точек (пиков).
Точка считается поворотной, если она больше предшествующей и последующей (или меньше).

E2= -0,692
0,765 >-0,692 > -1,145 - не является поворотной точкой
E3=-1,145
-0,692> -1,145< 1,307 – является поворотной точкой
E4= 1,307
-1,145< 1,307> 0,039 – является поворотной точкой
E5= 0,039
1,31> 0,039> 0,036 – не является поворотной точкой
E6= 0,036
0,039 >0,036> -0,69 - не является поворотной точкой
E7=-0,687
0,036 >-0,687 <1,581 - является поворотной точкой
E8=1,581
-0,687 <1,581 >-2,056 - является поворотной точкой
E9=-2,056
1,581> -2,056< 0,852 - является поворотной точкой
m=5

m=5>2, => неравенство выполняется, свойство выполняется.
Наличие (отсутствие) автокорреляции в отклонениях проверим с помощью критерия Дарбина-Уотсона. Предварительно по столбцу остатков с помощью функции СУММКВРАЗН определим что сумма разности квадратов равна 37,33, используем найденную нами сумму квадратов остатков – 12,02 и находим:
dw =  =
=  = 3,10
= 3,10
Фактическое значение d сравним с табличным значением при 5%-ном уровне значимости. При n= 10 и к= 1 (число факторов) нижнее значение d1 = 0,88, а верхнее d2= 1,32. Перед сравнением с табличными значениями dw критерий преобразуем по формуле dw’= 4- dw= 4-3,10=0,90
Так как 0,88<0,90<1,32 – область неопределенности, когда нет оснований ни принять, ни отвергнуть гипотезу о существовании автокорреляции.
Поскольку ситуация оказалась неопределенной, воспользуемся первым коэффициентом автокорреляции:
r(1) =  =
=  = -0,607
= -0,607
Так как фактическое значение коэффициента меньше табличного для 5% уровня значимости – 0,6319, то принимаем гипотезу об отсутствии автокорреляции.
Обнаружение гетероскедастичности. Чтобы оценить нарушение гомоскедастичности по тесту Голдфельда-Квандта, выполним следующие шаги:
- разделим упорядоченную по мере возрастания переменной х совокупность на две группы и определим по каждой из групп уравнений регрессии:


Определим остаточную сумму квадратов для первой и второй регрессии, используя данные таблицы:



Так как,  <
<  , то гетероскедастичность не имеет место.
, то гетероскедастичность не имеет место.
Соответствие ряда остатков нормальному закону распределения проверим с помощью R/S -критерия

где emax, emin - соответственно максимальный и минимальный уровни ряда остатков;
Se - среднеквадратическое отклонение.

Так как расчетное значение попадает между табулированными границами при уровне вероятности α =0,05: нижняя граница – 2,67 и верхняя граница – 3,57, то гипотеза о нормальном распределении ряда остатков принимается.
4. Осуществить проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента. (a=0,05).
Параметры уравнения: ta0 = -2,69, ta1 = 26,70 (фактические значения параметров).
Сравним данные параметры с табличными значениями: t табл (a; к), где к = n-m-1 = 8, a=0,05.
По условию а0 и а1 фактические должны быть больше табличных значений. tтабл = 2,31 => параметр а0 статистически значим, а а1 статистически не значим.
5. Вычислим коэффициент детерминации.
D=r2
Возьмем значения из таблицы – D=0,98, т.е. 98% вариации объемов продукции объясняется вариацией объемов капиталовложений. 2 % составляют факторы, которые оказывают влияние на величину объемов выпуска продукции (у), но не включены в модель регрессии.
Проверим значимость уравнения регрессии с помощью F – критерия Фишера (a=0,05).
Fфакт = 455,50, сравним с табличным значением F. Fтабл зависит от (а;к1;к2), где а – уровень значимости, а=0,05, к1 – число факторов (m) включенных в нашу модель (к1 = х=1), к2 = n-m-1 = 8.
Fтабл = 5,32. Сравним: Fтабл <Fфакт => построенное уравнение регрессии статистически значимо.
Найдем среднюю относительную ошибку аппроксимации.
Воспользуемся функцией АВS для расчёта средней ошибки аппроксимации. Воспользуемся функцией «Автосумма» и «Среднее значение» = > Е=3,19% <10% => построенная модель точная.
В среднем расчетные значения у для линейной модели отличаются от фактических значений на 3,19%
Так как ошибка аппроксимации данной модели меньше 10%, то это свидетельствует о хорошем качестве модели.
6. Осуществим прогнозирование среднего значения показателя Y при уровне значимости a=0,1, если прогнозное значение фактора X составляет 80% от его максимального значения.
y расч = 12,24 + 0,91*x.
Хпрогн=80%*хсред = 80%*23,5=18,8
y расч = 12,24 + 0,91* 18,8= 29,35 у.е.
Вывод: таким образом построено уравнение регрессии: y расч = 12,24 + 0,91*x – данная модель является точной (по параметру средней ошибки аппроксимации, статистически значимой (по F-критерию Фишера), по параметрам а0 модель статистически значима, а по а1 - статистически не значима (по критерию t-критерия Стбюдента). Но, в данной модели учтено всего 98% факторов оказывающих влияние на у (по коэффициенту детерминации). Связь между фактором х и результатом у – прямая, высокая (по коэффициенту корреляции).