МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
РОССИЙСКОЙ ФЕДЕРАЦИИ
РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
``````````````````````````````````````````````````````````````````````````````````````````````````````````
СБОРНИК ЗАДАЧ ПО ФИЗИКЕ
(для студентов педагогической специальности физических факультетов университетов)
Механика, часть IV

Ростов - на - Дону
Печатается по решению учебно-методической комиссии физического факультета
Протокол № от 2003 г.
Сборник задач по физике (для студентов педагогической специальности физических
факультетов университетов)., Л.М. Монастырский, В.И. Махно. - Ростов н/Д,
2003 г., стр. –15.
Сборник задач представляет собой четвертую часть задачника по курсу общей физики для студентов педагогической специальности физических факультетов университетов. Задачи подобраны с целью плавного перехода от курса физики, изучаемого в средней школе, к курсу общей физики.
Л.М. Монастырский
В.И. Махно

МОМЕНТ СИЛЫ
12.1.На тонкий прямоугольный брусок АВСД массы 10 кг действует вертикально направленная сила F, равная 20 Н (рис. 41). Определить векторы моментов силы F и силы тяжести относительно точек А и С. АВ=20 см, ВС=30 см.
 у
у
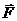
 В С
В С
 А Д
А Д
х
Рис. 41
12.2.Брусок А и сила F находятся в одной плоскости. Определить момент силы F относительно точки А (рис. 42). Чему равен момент силы F относительно осей x, y, z?
 у
у

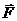
300


 А
А  х
х
Рис. 42
12.3.На плоский диск радиуса 50 см, лежащий на горизонтальной поверхности, действуют две силы F1=400 Н и F2=300 Н, направленные по касательной к диску в горизонтальной плоскости (рис. 43). Определить результирующую силу, действующую на диск, и результирующий момент сил относительно центра диска.
 |
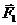
 Z
Z
 |

 |
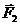
Рис. 43
12.4.Как изменится ответ в задаче № 11.3, если F1=F2? Найти величину перемещения диска за 10 с, если его масса 100 кг, а сила трения равна нулю.
12.5.Радиус блока 10 см, масса груза m= 5 кг, трением в оси блока пренебречь (рис. 44). Груз спускается с ускорением 2 м/с2. Найти: 1. Момент силы тяжести относительно оси блока. 2. Момент силы, вращающий блок, относительно оси блока.
 |

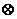 Z
Z
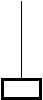 |
Рис. 44
12.6.Снаряд массы m начинает движение со скоростью v0, направленной под углом  к горизонту. Найти зависимость момента силы тяжести снаряда относительно точки выстрела от времени. Определить эту величину для моментов нахождения снаряда в высшей и наиболее удаленной точке траектории, если vо=40 м/с,
к горизонту. Найти зависимость момента силы тяжести снаряда относительно точки выстрела от времени. Определить эту величину для моментов нахождения снаряда в высшей и наиболее удаленной точке траектории, если vо=40 м/с,  =300.
=300.
12.7.Через блок радиуса R переброшен канат, на который действуют две силы F2 > F1, расположенные в плоскости, перпендикулярной оси блока (рис. 45). Определить вращающий момент и направление вращения блока.
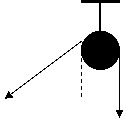 |


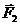
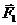
Рис. 45
12.8.Небольшое тело массы m находится посередине наклонной плоскости АВ ( = 300, АВ=L). Найти моменты сил, действующих на тело, относительно точки А, прямой АВ, оси Z (рис 46).
= 300, АВ=L). Найти моменты сил, действующих на тело, относительно точки А, прямой АВ, оси Z (рис 46).
 В
В

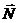

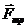
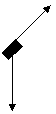


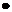 Z
Z
А 

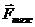


Рис. 46
12.9.К точкам 1 и 2 некоторого тела приложены две силы 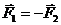 (пара сил). Найти результирующий момент относительно точек 1, 2, а также относительно произвольной точки 3 (рис. 47).
(пара сил). Найти результирующий момент относительно точек 1, 2, а также относительно произвольной точки 3 (рис. 47).

 1
1 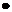
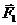
d

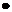 2
2
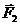
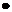 3
3
Рис. 47
12.10.Чему равен момент силы тяжести, действующей на космическую станцию “Мир”, относительно центра Земли. Какой вывод можно сделать из полученного результата?
12.11.Сила с компонентами (3, 4, 5) (Н) приложена к точке с координатами (4, 2, 3,) (м). Найти: а) момент силы 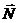 относительно начала координат; б) модуль вектора
относительно начала координат; б) модуль вектора 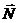 ; в) момент силы Nz относительно оси z.
; в) момент силы Nz относительно оси z.
12.12.Сила, приложенная к частице, имеет вид 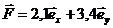 (Н). Чему равен момент этой силы относительно оси z, если точка приложения силы имеет координаты (4,2,6,8, 0).
(Н). Чему равен момент этой силы относительно оси z, если точка приложения силы имеет координаты (4,2,6,8, 0).
12.13.К точке, радиус-вектор которой относительно начала координат 0 равен 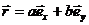 приложена сила
приложена сила 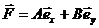 . Найти момент силы и плечо силы относительно
. Найти момент силы и плечо силы относительно
точки 0.
12.14.Математический маятник массы m, длины L колеблется в вертикальной плоскости. Максимальное отклонение от положения равновесия равно Lо. Как изменяется момент силы тяжести маятника относительно точки подвеса в процессе движения? Нарисовать график зависимости момента силы тяжести маятника относительно точки подвеса от величины угла  .
.
МОМЕНТ ИМПУЛЬСА
13.1.Определить относительно наблюдателя в точке 0 вектор момента импульса ракеты массы m, взлетающей вертикально со скоростью vо (рис. 48).

 |


 А
А
 Z
Z
0 
Рис. 48
13.2.Определить относительно точки выстрела момент импульса снаряда массы m в верхней точке траектории. Начальная скорость снаряда vо направлена под углом  к горизонту.
к горизонту.
13.3.Материальная точка массы m вращается в горизонтальной плоскости с постоянной угловой скоростью  по окружности радиуса r. Определить изменение модулей импульса и момента импульса точки относительно центра окружности за время, равное 0,25 периода вращения и 0,5 периода вращения..
по окружности радиуса r. Определить изменение модулей импульса и момента импульса точки относительно центра окружности за время, равное 0,25 периода вращения и 0,5 периода вращения..
13.4.Самолет летит на высоте Н параллельно поверхности Земли, его импульс равен р. Как при таком движении изменяется момент импульса самолета относительно наблюдателя, находящегося на поверхности Земли?
13.5.Математический маятник массы m, длина подвеса которого L, отвели на 900 относительно положения равновесия и отпустили, Найти зависимость момента импульса маятника относительно оси Z, проходящей через точку подвеса от угла  . Нарисовать график этой зависимости.
. Нарисовать график этой зависимости.
13.6.Тело массы m, радиус-вектор которого 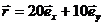 , движется со скоростью
, движется со скоростью 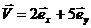 . Найти момент импульса тела относительно начала координат, относительно осей х, у, z.
. Найти момент импульса тела относительно начала координат, относительно осей х, у, z.
13.7.Тело массы 1кг, брошенное из точки с координатами (0, 2, 0) с начальной скоростью (0,0,10) возвращается в исходную точку. Найти: а) момент импульса тела как функцию времени относительно начала координат; б) изменение момента импульса за время полета относительно начала координат.
13.8.Небольшое тело массы m начинает скользить без трения с вершины наклонной плоскости (рис. 49). Найти относительно точки 0 выражения для: 1.Момента импульса тела в зависимости от времени. 2. Момента результирующей силы, действующей на тело.
 |
Н  Z
Z
0 


Рис. 49
13.9.Материальная точка массы m брошена под углом  к горизонту с начальной скоростью
к горизонту с начальной скоростью  .Найти относительно начала координат зависимость от времени: 1.Момента импульса частицы.2. Момента силы, действующей на частицу.
.Найти относительно начала координат зависимость от времени: 1.Момента импульса частицы.2. Момента силы, действующей на частицу.
13.10.Две частицы движутся равномерно в противоположных направлениях вдоль параллельных траекторий, расстояние между которыми равно L (рис. 50). Найти: 1.Суммарный импульс частиц. 2.Значение суммарных моментов импульса частиц относительно точек 01 и 02. Рассмотреть два случая: импульсы частиц различны по модулю и импульсы частиц одинаковы.


 Z
Z
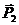

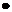
О1 b1 b2 О2

 |

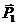
L
Рис. 50
13.11.Тело массы 100 г брошено с некоторой высоты в горизонтальном направлении со скоростью 20 м/с. Найти приращение моментов импульса тела относительно точки бросания за 5 с.
13.12.Момент импульса частицы относительно некоторой точки А зависит от времени по закону 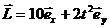 . Найти относительно точки А момент силы, действующий на частицу. Чему равен момент силы М, когда угол между
. Найти относительно точки А момент силы, действующий на частицу. Чему равен момент силы М, когда угол между 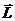 и
и 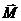 равен 600?
равен 600?
13.13.Частица массы m движется по окружности радиуса R так, что величина нормального ускорения зависит от времени по закону an=  t4. Определить: 1.Момент импульса частицы и момент силы, действующей на нее, относительно точки О.2.Момент импульса и силы относительно осей x,y,z.3.Представить графики зависимостей моментов импульса и силы от времени.
t4. Определить: 1.Момент импульса частицы и момент силы, действующей на нее, относительно точки О.2.Момент импульса и силы относительно осей x,y,z.3.Представить графики зависимостей моментов импульса и силы от времени.
13.14 Частица, положение которой относительно начала отсчета декартовой системы координат (точка 0) дается радиус-вектором 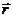 (-2, 1, -5) (м), имеет импульс
(-2, 1, -5) (м), имеет импульс 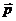 (1, 2, 3) (кгм/с). Определить: а) момент импульса частицы относительно точки 0; б) моменты импульса относительно осей x, y и z.
(1, 2, 3) (кгм/с). Определить: а) момент импульса частицы относительно точки 0; б) моменты импульса относительно осей x, y и z.
РАСЧЕТ МОМЕНТА ИНЕРЦИИ ТЕЛ ПРАВИЛЬНОЙ ФОРМЫ
14.1.Найти момент инерции математическго маятника относительно точки подвеса.
14.2.Найти момент инерции тонкого однородного стержня массы М и длины L относительно оси, перпендикулярной стержню и проходящей: 1.через один из его концов; 2.через середину стержня; 3. Через точку А, лежащую на продолжении стержня на расстоянии L от одного из его концов.
14.3.Найти момент инерции тонкого обода радиуса 0,2 м и массы 3 кг относительно оси, перпендикулярной плоскости обода и проходящей: 1.через центр тяжести обода; 2.через конец диаметра.
14.4.Определить момент инерции диска массы m, радиуса R относительно оси, перпендикулярной плоскости диска и проходящей через край диска.
14.5.Определить момент инерции сплошного шара радиуса R и массы m относительно оси, проходящей: 1.через центр тяжести; 2.по касательной к шару.
14.6.Определить момент инерции полого шара массы m относительно оси, проходящей через центр тяжести. Внешний радиус шара R, внутренний – r.
14.7.Определить момент инерции тонкого кольца радиуса R и массы m относительно оси, проходящей через центр тяжести и лежащей в плоскости обода.
14.8.Определить момент инерции шайбы, радиусы которой r и R, относительно оси, перпендикулярной плоскости шайбы и проходящей через ее центр масс.
14.9.Определить момент инерции сплошного цилиндра радиуса R, массы m относительно оси цилиндра.
14.10.Определить момент инерции полого цилиндра массы m, внутренний радиус которого r, внешний R.
14.11.Определить момент инерции фигур, изготовленных из тонких стержней массы m, длины L относительно осей, перпендикулярных плоскости рисунка и проходящих через указанные точки (рис. 51).
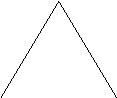 |





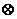
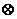
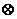



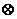
а) б) в)
Рис. 51
14.12.Определить момент инерции тонкой прямоугольной пластинки (масса m, стороны 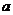 и
и 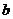 ) относительно оси, проходящей через центр тяжести параллельно одной из сторон.
) относительно оси, проходящей через центр тяжести параллельно одной из сторон.
14.13. Определить момент инерции тонкой прямоугольной пластинки (масса m, стороны 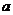 и b) относительно оси, проходящей через центр тяжести перпендикулярно плоскости пластинки.
и b) относительно оси, проходящей через центр тяжести перпендикулярно плоскости пластинки.
14.14.В тонком диске массой m и радиусом R вырезают n круглых отверстий радиуса r на равных расстояниях a от центра диска. Определить момент инерции диска относительно оси, проходящей через его центр масс.
14.15.Цилиндр массы 3 кг, диаметр которого 12 см, лежит на горизонтальной плоскости. Определить момент инерции цилиндра относительно оси, проходящей по линии контакта его боковой поверхности с плоскостью.
14.16.Кинолента наматывается на бобину со скоростью V. Момент инерции бобины без ленты Iо, радиус rо. Определить зависимость момента инерции катушки с лентой от времени. Ширина ленты 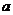 , плотность
, плотность 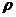 , толщина b.
, толщина b.
14.17.Две частицы с одинаковой массой m соединены жестким однородным стержнем длины L и массы m1. Найти момент инерции этой системы относительно оси, перпендикулярной стержню и проходящей через: 1.центр масс системы; 2.одну из частиц.
14.18.Поверхностная плотность тонкого диска радиуса R изменяется по закону 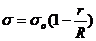 . Найти момент инерции диска относительно оси, проходящей через центр диска перпендикулярно его плоскости.
. Найти момент инерции диска относительно оси, проходящей через центр диска перпендикулярно его плоскости.
14.19.Прямой круглый однородный конус имеет массы m и радиус основания R. Найти момент инерции конуса относительно его оси.
14.20.Найти момент инерции однородного куба относительно оси, проходящей через центры противолежащий граней. Масса куба m, длина ребра L.
14.21.Вычислить момент инерции однородного круглого прямого цилиндра относительно оси, перпендикулярной к оси симметрии цилиндра и проходящей через его центр. Масса цилиндра m, радиус R, высота h. Рассмотреть предельные случаи: R << h, h << R.
14.22.Найти момент инерции однородной пирамиды, основанием которой является квадрат со стороной 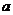 , относительно оси, проходящей через вершину и центр основания. Масса пирамиды равна m.
, относительно оси, проходящей через вершину и центр основания. Масса пирамиды равна m.
15.ДИНАМИКА ТВЕРДОГО ТЕЛА, ВРАЩАЮЩЕГОСЯ ВОКРУГ
НЕПОДВИЖНОЙ ОСИ
15.1. Найти ускорение грузов и натяжение нитей на машине, изображенной на рис. 52, учитывая момент инерции I блока, при условии, что нить не скользит по блоку. Определить натяжение подвеса А.
 |
А
 |

 I, r
I, r
 |
 m2
m2
m1
Рис. 52
15.2. На однородный сплошной цилиндр массы М и радиуса R плотно намотана легкая нить, к концу которой прикреплен груз массы m (рис. 54). В момент времени t=0 система пришла в движение. Пренебрегая трением в оси цилиндра, найти:1. Зависимость угловой скорости от времени; 2. Направление векторов 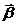 и
и 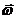 ; 3. Ускорение груза; 4. Силу натяжения нити; 5. Для системы блок-груз зависимость от времени момента импульса относительно оси блока и кинетической энергии; 6. Углы поворота блока в зависимости от времени.
; 3. Ускорение груза; 4. Силу натяжения нити; 5. Для системы блок-груз зависимость от времени момента импульса относительно оси блока и кинетической энергии; 6. Углы поворота блока в зависимости от времени.
 |
 М
М
 |
m
Рис. 54
15.3.Через блок радиуса 10 см, масса которого m=100 г, перекинута тонкая гибкая нерастяжимая нить, к концам которой подвешены два груза массами m1=200 г и m2=300 г (рис. 55). Определить: 1. Ускорения грузов; 2. Угловое ускорение; 3. Силы натяжения нитей.
 |
 m2
m2
 |
m1
Рис. 55
15.4. Однородный цилиндр массы М и радиуса R вращается вокруг горизонтальной оси, проходящей через его центр масс, под действием грузов весом Р каждый. Найти силу натяжения нити на участках 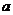 и
и 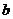 (рис. 56).
(рис. 56).
 |
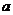
 Р
Р
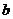
 Р
Р
Рис. 56
15.5. На ступенчатый блок намотаны в противоположных направлениях две нити (рис 57). На конец одной нити действуют постоянной силой F, а к концу другой нити прикреплен груз массы m. Известны радиусы R1 и R2 блока и его момент инерции I относительно оси вращения. Найти угловое ускорение блока.
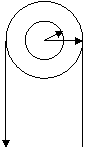 |

Рис. 57
15.6. На горизонтальном столе лежат два тела, которые могут скользить по столу без трения. Тела связаны невесомой нерастяжимой нитью (рис. 58). Такая же нить, переброшенная через блок, связывает тело 2 с грузом массы m=0,5 кг. Блок представляет собой однородный сплошной цилиндр. Масса тел и блока одинакова и равна М=1 кг. Считая, что блок вращается без трения, а нить не проскальзывает по блоку, найти ускорение тел, натяжение F12 нити, связывающей оба тела, натяжение нити F2 на участке от тела 2 до блока, натяжение нити Fm на участке от блока до груза m.
1 2

 М F1 М F2 М
М F1 М F2 М
 |
Fm

m
Рис. 58
15.7. Однородный сплошной цилиндр массы m=1 кг висит в горизонтальном положении на двух намотанных на него невесомых нитях (рис. 59). Цилиндр опускается без толчка. А). За сколько времени t цилиндр опустится на расстояние h=50 см? б) Какое натяжение F испытывает при этом каждая из нитей?

Рис. 59
15.8. Система, состоящая из цилиндрического катка радиуса R и гири, связанных нитью, перекинутой через блок (рис. 60) под действием силы тяжести приходит в движение из состояния покоя. Определить ускорение a центра масс катка и силу натяжения нити. Какую скорость приобретет гиря, если она опускается с высоты h? Масса цилиндра М, масса гири m, массой блока пренебречь. Каток катится без скольжения.
 |

 М
М
 | |||
 | |||
 m
m
Рис. 60
15.9. Из колодца с помощью ворота поднималось ведро с водой массы m. В момент, когда ведро находилось на высоте h от поверхности воды, рукоятка освободилась, и ведро стало двигаться вниз. Определить линейную скорость рукоятки в момент удара ведро о поверхность воды в колодце, если радиус рукоятки R, радиус вала ворота r, его масса m1. Трением и весом торса пренебречь.
15.10. К концу тонкой нерастяжимой нити, намотанной на цилиндрический сплошной блок массой m1=200 г, прикреплено тело массой m2=500 г, которое находится на наклонной плоскости с углом наклона 450 (рис. 61). Нить, удерживающая тело, параллельна наклонной плоскости. Какой путь пройдет тело по наклонной плоскости за t=1 с, если коэффициент трения скольжения по наклонной плоскости равен k=0,1?
 |

 m1
m1
 |
 m2
m2


Рис. 61
15.11. По наклонной плоскости, образующей угол  с горизонтом, скатывается без скольжения сплошной однородный диск. Найти линейное ускорение
с горизонтом, скатывается без скольжения сплошной однородный диск. Найти линейное ускорение 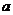 центра диска.
центра диска.
15.12. Какой путь пройдет катящийся без скольжения диск, поднимаясь вверх по наклонной плоскости с углом наклона 300,если ему сообщена начальная скорость 7 м/с, параллельная наклонной плоскости.
15.13. Найти ускорение центра однородного шара, скатывающегося по наклонной плоскости, образующей угол  с горизонтом. Чему равна сила трения шара о плоскость?
с горизонтом. Чему равна сила трения шара о плоскость?
15.14. Шар скатывается по наклонной плоскости с углом наклона 300. Какую скорость будет иметь центр шара относительно наклонной плоскости через 1,5 с, если его начальная скорость была равна нулю?
15.15. По наклонной плоскости, составляющей с горизонтом угол 300, скатывается без скольжения сплошной цилиндр, масса которого равна 300 г. Найти величину силы трения цилиндра о плоскость.
15.16. С одного уровня наклонной плоскости одновременно начинают скатываться сплошной цилиндр и шар одинаковых радиусов. 1)Какое тело будет иметь 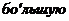 скорость на данном уровне? 2)Во сколько раз? 3)Во сколько раз скорость одного будет больше скорости другого в данный момент времени?
скорость на данном уровне? 2)Во сколько раз? 3)Во сколько раз скорость одного будет больше скорости другого в данный момент времени?