1) Уравнение плоской бегущей волны
y = A cos  (t – x/
(t – x/  ),
),
где y – смещение любой из точек среды с координатой x в момент t;  – скорость распространения колебаний в среде.
– скорость распространения колебаний в среде.
2) Связь разности фаз Dj колебаний с расстоянием между точками среды, отсчитанным в направлении распространения колебаний:
 = (2
= (2  /
/  )
)  x,
x,
где l – длина волны.
3) Фазовая скорость распространения электромагнитных волн в среде
 ,
,
где с – скорость электромагнитных волн в вакууме, с =  108 м/c.
108 м/c.
4) Связь длины электромагнитной волны с периодом Т и частотой  колебаний
колебаний
 или
или  .
.
5) В плоской электромагнитной волне
E  =
= 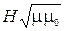 .
.
6) Вектор Пойнтинга
П = [  ].
].
Модуль вектора Пойнтинга равен плотности потока энергии электромагнитной волны.
Примеры решения задач
Задача 1
Плоская волна распространяется в упругой среде со скоростью 100 м/с. Наименьшее расстояние между точками среды, фазы колебаний которых противоположны, равно 1м. Определить период колебаний и частоту.
Дано:
 = 1м = 1м
 = 100м/с = 100м/с
| Решение: Точки, находящиеся друг от друга на расстоянии, равном длине волны, колеблются с разностью фаз, равной 2p. Точки, находящиеся друг от друга на любом расстоянии, колеблются с разностью фаз, равной |
Т =? 
|
 (1)
(1)
Решая это равенство относительно l, получаем
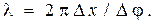 (2)
(2)
По условию задачи Dj = p. Подставляя значения величин, входящих в выражение (2), получим:
 м.
м.
Скорость  распространения волны связана с l и Т отношением
распространения волны связана с l и Т отношением
 , (3)
, (3)
где  – частота колебаний.
– частота колебаний.
Из выражения (3) получаем  .
.
Произведем вычисления:
 = (100 / 2) = 50 Гц, Т = 1/50 с = 0,02 с.
= (100 / 2) = 50 Гц, Т = 1/50 с = 0,02 с.
5.2.6. Интерференция света
1) Скорость света в среде
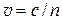 ,
,
где с – скорость света в вакууме; n – показатель преломления среды.
2) Оптическая длина пути световой волны
L = nl,
где l – геометрическая длина пути световой волны в среде с показателем преломления n.
3) Оптическая разность хода двух световых волн
 = L 1 – L 2.
= L 1 – L 2.
4) Связь разности фаз колебаний  с оптической разностью хода
с оптической разностью хода
 ,
,
где l – длина световой волны в вакууме.
5) Условие максимального усиления света при интерференции
 =
=  , к = 0, 1, 2…
, к = 0, 1, 2…
Условие максимального ослабления света при интерференции
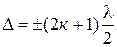 .
.
6) Оптическая разность хода световых волн, возникающая при отражении монохроматического света от тонкой пленки:
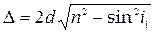 -
-  =
=  ,
,
где d – толщина пленки; n – показатель преломления пленки; i 1 – угол падения; i 2 – угол преломления света в пленке.
Разность хода – l/2 возникает при отражении света от оптически более плотной среды.
7) Радиус светлых колец Ньютона в отраженном свете
r  , к = 1, 2, 3…,
, к = 1, 2, 3…,
где к – номер кольца; R – радиус кривизны; n – показатель преломления среды, находящейся между линзой и стеклянной пластинкой.
Радиус темных колец Ньютона в отраженном свете
r  , к = 0, 1, 2…
, к = 0, 1, 2…
Примеры решения задач
 |
Задача 1
Расстояние между двумя когерентными источниками равно 0,9 мм. Источники, испускающие монохроматический свет с длиной волны 640 нм, расположены на расстоянии 3,5 м от экрана. Определить число светлых полос, которые наблюдаются на 1 см длины экрана.
Дано:
λ = 640 нм = 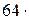 10-8 м
d = 0,9 мм = 10-8 м
d = 0,9 мм =  10-4 м
L = 3,5 м 10-4 м
L = 3,5 м
| Решение: В точке О на экране (рис. 2) будет максимальная освещенность: точка О равноудалена от обоих источников SI и SII, поэтому разность хода волн SIО и SIIО равна нулю. В произвольной точке экрана Ок максимум освещенности будет наблюдаться, если оптическая разность хода когерентных волн равна целому числу длин волн: |
 ? ?
|
D = S 2 – S 1 = к l, (1)
где S 2, S 1 – оптические пути интерферирующих волн;l – длина волны падающего света; к – номер светлой полосы (центральная светлая полоса принята за нулевую). Оптическая разность хода волн D = xd/L, где x – расстояние от центральной светлой полосы до к -й светлой полосы.



 Ок
Ок
S1
SI О1 O1
О
d S2
SII O2
L
Рис. 10
Учитывая выражение (1), получим:
 . (2)
. (2)
Из выражения (2) определяем искомую величину  – число светлых интерференционных полос на 1 см длины:
– число светлых интерференционных полос на 1 см длины:
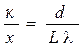 .
.
Подставим в это выражение числовые значения и получим:
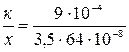 = 400 м-1 ,
= 400 м-1 ,
откуда  на 1 см равно 4.
на 1 см равно 4.
Пример 2
Для устранения отражения света от поверхности линзы на нее наносится тонкая пленка вещества с показателем преломления(n = 1,26), меньшим, чем у стекла (просветление оптики). При какой наименьшей толщине пленки отражение света с длиной волны 0,55 мкм не будет наблюдаться, если угол падения лучей 30о?
| Дано: n = 1,26 λ = 0,55 мкм =5,5∙10-7 м i 1 = 30о | Решение:
 Рис. 3 Рис. 3
|
 ? ?
|
Оптическая разность хода лучей, отраженных от верхней и нижней поверхностей пленки (рис. 3), равна
D = 2 d  , (1)
, (1)
где d – толщина пленки; n – показатель преломления пленки; i 1 – угол падения лучей.
В выражении (1) учтено, что отражение лучей на верхней и нижней поверхностях пленки происходит от оптически более плотной среды и поэтому потери полуволны в обоих случаях компенсируют друг друга.
Условие интерференционного минимума
 . (2)
. (2)
Из (1) и (2) находим
 . (3)
. (3)
Полагая к = 0, 1, 2, 3...., получим ряд возможных значений толщины пленки. Минимальная толщина пленки будет при к = 0.
Подставим в расчетную формулу (3) числовые значения входящих величин: n = 1,26; l = 0,55 мкм = 5,5  -7 м; i1 = 30о; к = 0.
-7 м; i1 = 30о; к = 0.
Произведем вычисления:
 мкм.
мкм.
5.2.7. Дифракция света
1) Радиус к -й зоны Френеля:
- для сферической волны
r  ,
,
где a – расстояние между диафрагмой с круглым отверстием и точечным источником света; b – расстояние между диафрагмой и экраном, на котором ведется наблюдение дифракционной картины; к – номер зоны Френеля; l – длина волны.
- для плоской волны
r  .
.
2) Дифракция света на одной щели при нормальном падении света (дифракция Фраунгофера).
Угол j отклонения лучей, соответствующих минимуму интенсивности света, определяется из условия
a sin  , к = 0, 1, 2 …,
, к = 0, 1, 2 …,
где a – ширина щели; к – порядковый номер минимума; l – длина волны.
Угол j отклонения лучей, соответствующий максимуму интенсивности света, определяется из условия
a sin  , к = 0, 1, 2 …,
, к = 0, 1, 2 …,
где j – приближенное значение угла дифракции.
3) Дифракция света на дифракционной решетке при нормальном падении лучей.
Условие главных максимумов интенсивности
d sin 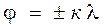 , к = 0, 1, 2 …,
, к = 0, 1, 2 …,
где d – период (постоянная решетки); к – номер главного дифракционного максимума в случае монохроматического света или порядок спектра в случае белого света; j – угол отклонения лучей, соответствующий максимуму интенсивности.
4) Разрешающая способность дифракционной решетки
R =  = к N,
= к N,
где Dl – наименьшая разность длин волн двух соседних спектральных линий (l и l + Dl), при которой эти линии могут быть видны раздельно в спектре, полученном посредством данной решетки; N – число щелей решетки.
5) Формула Вульфа-Брэггов:
2 d sin  ,
,
где q – угол скольжения (угол между направлением параллельного пучка рентгеновского излучения, падающего на кристалл, и атомной плоскостью в кристалле); d – расстояние между атомными плоскостями кристалла.
Примеры решения задач
Пример 1
На дифракционную решетку длиной 10 мм, имеющую 400 штрихов на 1 мм, падает нормально свет от разрядной трубки. Помещенная вблизи решетки линза проецирует дифракционную картину (рис. 4) на плоский экран Э, удаленный от линзы на расстояние 1м. Определить: 1) ширину спектра первого порядка, если границы видимого спектра составляют 780 нм (красный край спектра) и 400 нм (фиолетовый край спектра); 2) число спектральных линий красного цвета, которые теоретически можно наблюдать с помощью данной дифракционной решетки; 3) в спектре какого порядка эта решетка может разрешить две линии с длиной волны, равной 500 нм и 500,1 нм?
Дано:
l 0 = 10 мм = 10-2 м
n = 400 мм-1= 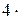 105 м-1
L = 1 м 105 м-1
L = 1 м
 кр = 780 нм = кр = 780 нм = 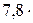 10-7 м 10-7 м
 ф = 400 нм = ф = 400 нм = 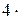 10-7 м 10-7 м
 1 = 500 нм = 1 = 500 нм =  10-7 м 10-7 м
 2 = 500,1 нм = 2 = 500,1 нм =  10-7 м 10-7 м
| Решение:
Угол j отклонения лучей, соответствующий максимуму фиолетового цвета при дифракции света на решетке, определяется из условия
d sin  1 = к 1 = к 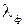 (к = 1), (1)
следовательно,
sin (к = 1), (1)
следовательно,
sin  = =  (2) (2)
|
| l 1 =? к кр =? к =? |
Аналогично для дифракционного максимума красного цвета получим:
sin 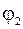 =
=  . (3)
. (3)
Из рис. 4 следует, что расстояние от центра дифракционной картины до фиолетовой спектральной линии равно
l 1 = L tg  (4)
(4)
соответственно для красной спектральной линии
l 2 = L tg 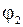 . (5)
. (5)
l0
 |
линза

 L
L
Э
l1
l2
Рис. 4
Ширина спектра первого порядка будет Δ l = l 2 – l 1 или с учетом формул (4) и (5)
Δ l = L (tg 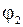 –tg
–tg  ). (6)
). (6)
В случае малых углов 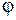 , что имеет место для спектра первого порядка
, что имеет место для спектра первого порядка
tg 
 sin
sin  .
.
Поэтому, подставив выражения (2) и (3) в формулу (6), получим:
 (7)
(7)
Зная число штрихов n на 1 мм решетки, найдем период решетки:
d =  . (8)
. (8)
Подставляя (8) в формулу (7), получим:
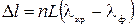 . (9)
. (9)
Произведем вычисления
 м = 15,2 см.
м = 15,2 см.
Для определений числа спектральных линий красного цвета найдем максимальное значение кmах, исходя из того, что максимальный угол отклонения лучей не может превышать 90° (sin 90° = 1). Из формулы (1) напишем:
к =  ,
,
следовательно, кmax  . С учетом (8) получим:
. С учетом (8) получим:
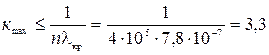 .
.
Так как число кmах должно быть обязательно целым, то кmах = 3. Влево и вправо от центра картины будет наблюдаться одинаковое число спектральных линий, равное 2 кmах. Таким образом, общее число спектральных линий равно 2 кmах = 6.
Так как разрешающая способность дифракционной решетки
R =  = кN,(10)
= кN,(10)
то минимальная разница длин волн двух спектральных линий, разрешаемых решеткой,
 . (11)
. (11)
Две спектральные линии разрешены, если
 . (12)
. (12)
Полагая l = l1, получаем
 . (13)
. (13)
Из выражения (13) следует, что спектральные линии разрешены в спектрах с порядком
 . (14)
. (14)
Число щелей решетки определяется выражением 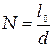 , или с учетом формулы (8)
, или с учетом формулы (8)
N =  n. (15)
n. (15)
Подставляя (15) в (14), получим:
 . (16)
. (16)
Произведем вычисления
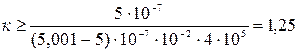 .
.
Так как к – целое число, то к  2.
2.
5.2.8. Поляризация света
1) Закон Брюстера
tg  = n 21,
= n 21,
где i 1 – угол падения, при котором отразившийся от диэлектрика луч полностью поляризован; n 21 = n 2 /n 1 – относительный показатель преломления второй среды относительно первой.
2) Закон Малюса
I = In cos 2  ,
,
где In – интенсивность плоскополяризованного света, падающего на анализатор; I – интенсивность этого света после анализатора; a – угол между направлением колебаний светового вектора волны, падающей на анализатор и плоскостью пропускания анализатора (плоскостью поляризации).
3) Угол поворота плоскости поляризации монохроматического света при прохождении через оптически активное вещество:
- в твердых телах

где a – постоянная вращения; d – длина пути, пройденного светом в оптически активном веществе;
- в растворах

где a0 – удельное вращение;  – массовая концентрация оптически активного вещества в растворе.
– массовая концентрация оптически активного вещества в растворе.
Примеры решения задач
Пример 1
Во сколько раз уменьшится интенсивность естественного света при прохождении через две призмы Николя, угол между плоскостями поляризации которых равен 60o. Потери света в каждой призме составляют 10 % (рис. 5).
 A I 1
A I 1
I 0 I 2
 |
N 1 B N 2
Рис. 5
Дано:
 = 60о
к = 0,1 = 60о
к = 0,1
| Решение: В результате двойного лучепреломления естественный луч света, попадая на первую призму Николя (поляризатор), раздваивается на обыкновенный “о” и необыкновенный “е” лучи. Оба луча поляризованы вовзаимноперпендикулярных плоскостях. |
 =? =?
|
Обыкновенный луч, подчиняясь закону преломления, преломляется и, подойдя к слою канадского бальзама в призме (граница АВ), испытывает полное отражение и поглощается зачерненной боковой гранью призмы. Необыкновенный луч проходит через призму. Таким образом, на выходе поляризатора получается плоскополяризованный свет, интенсивность которого с учетом потерь на отражение и поглощение света поляризатором равна
 ,(1)
,(1)
где I 0 – интенсивность естественного света, падающего на поляризатор; к – коэффициент, учитывающий потери на отражение и поглощение.
Плоскополяризованный луч света, падая на вторую призму Николя (анализатор), также расщепляется на обыкновенный и необыкновенный лучи. Обыкновенный луч полностью поглощается призмой. Необыкновенный луч проходит через призму. После прохождения анализатора интенсивность света уменьшается как за счет отражения и поглощения света анализатором, так и из-за несовпадения плоскости поляризации света с плоскостью пропускания анализатора. В соответствии с законом Малюса и с учетом потерь на отражение и преломление света интенсивность равна
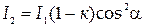 , (2)
, (2)
 |
где a – угол между плоскостями поляризации поляризатора и анализатора. Подставляя выражение (1) в (2), имеем
 . (3)
. (3)
Относительное уменьшение интенсивности света при прохождении света через 2 призмы Николя равно
 . (4)
. (4)
Подставив в расчетную формулу (4) значение к = 0,1; α = 60о, получим:  = 9,88.
= 9,88.