Пример 4:
Даны комплексные числа  ,
,  . Найти частное
. Найти частное 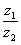 .
.
Составим частное:

Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение.
Вспоминаем формулу 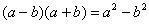 и смотрим на наш знаменатель:
и смотрим на наш знаменатель: 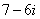 . В знаменателе уже есть
. В знаменателе уже есть 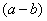 , поэтому сопряженным выражением в данном случае является
, поэтому сопряженным выражением в данном случае является 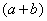 , то есть
, то есть 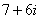
Согласно правилу, знаменатель нужно умножить на 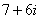 , и, чтобы ничего не изменилось, домножить числитель на то же самое число
, и, чтобы ничего не изменилось, домножить числитель на то же самое число 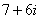 :
:

Далее в числителе нужно раскрыть скобки (перемножить два числа по правилу, рассмотренному в предыдущем пункте). А в знаменателе воспользоваться формулой 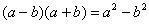 (помним, что
(помним, что 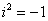 и не путаемся в знаках!!!).
и не путаемся в знаках!!!).
Распишу подробно:
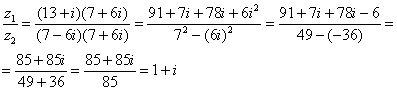
Пример подобран «хороший», если взять два произвольных числа, то в результате деления почти всегда получатся дроби, что-нибудь вроде  .
.
Примеры решения задач
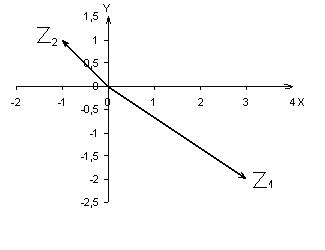
1) Построить на координатной плоскости числа Z1, Z2, где Z1=3-2i, Z2=-1+i.
Решение
На координатной плоскости изобразим точки (3; -2), (-1; 1) и соединим их с началом
координат, получив векторы, конечными точками которых являются заданные точки.
2) Выполнить действия сложения, вычитания, умножения, деления над комплексными числами в алгебраической форме.
Z1=3+4i, Z2=2i18-5i15
Решение
Предварительно преобразуем второе число, используя значения степеней мнимой единицы. i18=i16+2=i16i2=1i2=-1, i15=i12+3=i12i3=i3=-i, Z2=-2+5i
Выполним действия над числами:
Z1+Z2=(3+4i)+(-2+5i)=3+4i-2+5i=(3-2)+(4i+5i)=1+9i
Z1-Z2=(3+4i)-(-2+5i)=3+4i+2-5i=(3+2)+(4i-5i)=5-I
Z1 .Z2=(3+4i) . (-2+5i)=-6+15i – 8i +20i2=-6+7i – 20= - 26 + 7i

3) Представить число в тригонометрической форме Z= 
Найдем модуль и аргумент комплексного числа

Раздел 4. Элементы теории вероятностей и математической статистики
Изучить по учебной литературе вопросы:
1. Случайные события, их виды. Вероятность случайного события, способы ее получения.
2. Комбинаторика. Применение элементов комбинаторики к вычислению вероятности.
3. Действия над случайными событиями, вычисление вероятностей результатов действий.
4. Случайные величины, их виды. Закон распределения случайной величины
5. Ряд и функция распределения дискретной случайной величины.
6. Математическое ожидание дискретной случайной величины.
7. Дисперсия дискретной случайной величины.
Случайные события и их вероятности.
Математическая статистика.
Применение комбинаторики к подсчету вероятности.
Пример 1:
В партии из N деталей имеется n бракованных. Какова вероятность того, что среди наудачу отобранных k деталей окажется s бракованных?
Решение.
Количество всех элементарных исходов равно  . Для подсчета числа благоприятных случаев рассуждаем так: из n бракованных можно выбрать s деталей
. Для подсчета числа благоприятных случаев рассуждаем так: из n бракованных можно выбрать s деталей  способами, а из N – n небракованных можно выбрать
способами, а из N – n небракованных можно выбрать
k – s небракованных деталей  способами; по правилу произведения число благоприятных случаев равно
способами; по правилу произведения число благоприятных случаев равно 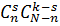 . Искомая вероятность равна:
. Искомая вероятность равна:
p = 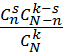 (1)
(1)
Замечание:
Всякое k-членное подмножество n-членного множества называется сочетанием из n элементов по k.
Число различных сочетаний из n элементов по k обозначается 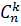 .
.
Справедлива формула
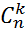 =
= 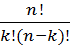 , (2)
, (2)
n! =1 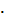 2
2 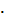 3
3  4
4  …
…  n
n
Пример 2:
В партии из 12 деталей имеется 7 стандартных. Найти вероятность того, что среди шести взятых наугад деталей 4 стандартных.
Решение.
Искомую вероятность найдем по формуле (1) для случая
N =12, n =7, k = 6, s = 4.
p = 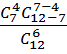 =
= 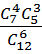 =
= 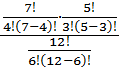 =
= 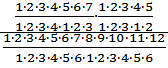
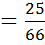 .
.
Пример 3:
Имеется набор разноцветных шариков, среди которых 5 синих, 3 красных и 2 зеленых. Наугад извлекают 4 шарика. Найти вероятность того, что среди извлеченных шариков 2 синих, 1 красный и 1 зеленый.
Решение
Для определения вероятности случайного события будем использовать классическую формулу 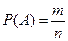 , в которой n – число всех возможных исходов, m- число исходов, благоприятных появлению события. В задаче значения этих величин следует находить при помощи сочетаний.
, в которой n – число всех возможных исходов, m- число исходов, благоприятных появлению события. В задаче значения этих величин следует находить при помощи сочетаний. 
Пример 4:
Из карточек разрезной азбуки составлено слово «панорама». Карточки перемешали и наудачу по одной извлекают 5 карточек, выкладывая их в порядке извлечения. Найти вероятность того, что окажется составленным слово «роман».
Решение
В этой задаче можно воспользоваться произведением зависимых случайных событий
А – получение слова «роман»; В1 – извлечение первой карточки с буквой «р»;
В2 – извлечение второй карточки с буквой «о»; и т.д. Тогда А=В1 . В2 . В3 . В4 . В5
Р(А)=Р(В1) . Р(В2) . Р(В3) . Р(В4) . Р(В5)= 
Пример 5:
В трех ящиках имеется по 6 одинаковых изделий, среди которых соответственно 2,
1, 3 бракованных. Наугад из каждого ящика извлекают по одному изделию. Найти вероятность того, что среди них окажутся два качественных и одно бракованное изделия.
Решение
Для решения задачи рассмотрим события: А – извлечение двух качественных и одного бракованного изделий, В1 – извлечение качественного изделия из первого ящика;
В2 – извлечение качественного изделия из второго ящика; В3– извлечение качественного изделия из третьего ящика; извлечение бракованного изделия для каждого ящика является событиями 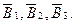 Составим событие А и вычислим его вероятность
Составим событие А и вычислим его вероятность
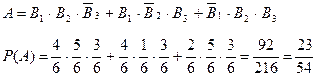
Пример 6:
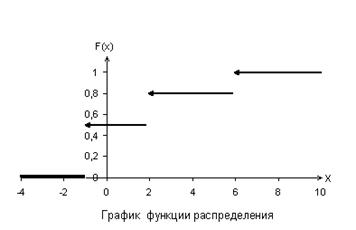
Вычислить математическое ожидание и дисперсию случайной величины, составить функцию распределения, начертить многоугольник распределения и график функции распределения. Имеется заданный ряд распределения дискретной случайной величины
| хi | -1 | ||
| pi | 0,5 | 0,3 | 0,2 |
Для вычисления математического ожидания воспользуемся формулой 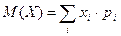
Получим M(X)=(-1).0,5+2.0,3+6.0,2=1,3
Для вычисления дисперсии воспользуемся двумя соотношениями, одно из которых соответствует определению дисперсии, другое – ее свойству.
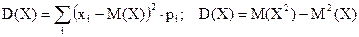
В примере получим: D(X)=(-1-1,3)2 . 0,5+(2-1,3)2 . 0,3+(6-1,3)2 . 0,2=7,21
M(X2)=(-1)2 . 0,5+22 . 0,3+62 . 0,2=8,9
D(X)= 8,9 – 1,32 =7,21 (значения должны совпадать)
Для построения многоугольника распределения нужно на координатной плоскости построить точки (xi;pi) и последовательно их соединить отрезками.
Для построения функции распределения воспользуемся схемой:
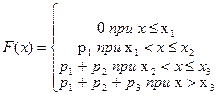
В примере получим 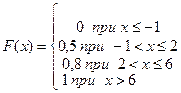
Используя значения заданного примера получим графики: