Эскиз магнитной системы и размещения на ней обмоток.

Расчет магнитной цепи,

Параметров холостого хода

И короткого замыкания трансформаторов.

 

 

Выполнил:
Группа:
Проверил:

 

 

Москва 2017

Таблица исходных данных.

 

Вариант
Общие данные
Мощность	S = 100 кВА
Схема и группа соединений	Y/ Y -0
Частота	f=50
Номинальные напряжения	Высокое напряжение	UномВН=3300В
Низкое напряжение	UномНН=230В
Число витков	Высокое напряжение	WBH=605
Низкое напряжение	WHH=42
Сечение витка	Высокое напряжение	SBH = 10,9 мм2
Низкое напряжение	SHH = 192,5 мм2
Внутренний диаметр	D1= 12.4 см
Радиальные размеры	Высокое напряжение	а2 = 3.15 см
Низкое напряжение	a1 = 2,2 см
Канал между обмотками ВН и НН	a12=l.1 см
Высота обмотки	l1 =l2 =49,5 см
Магнитная система
Диаметр стержня	d= 11.5см
Активное сечение	Стержень	Пс=90,2см2
Ярмо	Пя =107.9 см2
Высота	Стержень	hc =53,5 см
Ярмо	hя =11.5 см
Расстояние между осями С	С = 26,0 см
Бак
Масса масла	mмасла =210 кг
Масса бака	mбака =150 кг
Контрольные данные
Потери при КЗ	Рк= 1970 Вт
Потери при XX	Рх=365Вт
Напряжение КЗ	UK=4,5 %
Ток XX	I0 = 2,6 %
Напряжение нулевой последовательности	Uнп. = 50%

Обмотка трансформатора алюминиевая. Магнитная система собрана впереплет, с косыми стыками над крайними стержнями и прямым над средним стержнем, из холоднокатаной стали марки 3404 - 0,35 мм по ГОСТ 21427-83. Напряжение нулевой последовательности в процентах от номинального фазного отнесено к току нулевой последовательности, равному номинальному току. Обмотка НН соединена по схеме звезда с нулевым выводом.

1. Определить:

- фазные значения номинального напряжения, а так же номинальный ток и его фазные значения на сторонах ВН и НН, и коэффициент трансформации (для средней ступени напряжения ВН).

Фазное значение высокого напряжения трехфазного трансформатора (при соединении обмоток в «звезду»):

Фазное значение низкого напряжения трехфазного трансформатора (при соединении обмоток в «звезду»):

Номинальный линейный и фазный ток обмотки ВН (при соединении обмоток в «звезду»):

Номинальный линейный и фазный ток обмотки НН (при соединении обмоток в «звезду»):

Линейный и фазный коэффициент трансформации трансформатора при соединении Y/ Y -0:

Эскиз магнитной системы и размещения на ней обмоток.

Рисунок 1 – Эскиз магнитной системы трансформатора:

1 - Обмотка НН 2- Обмотка ВН.

Вычерчивается схема соединения обмоток, обеспечивающая получение заданной группы соединения.

Рисунок 2 – Схема соединения обмоток трансформатора (а)

и векторная диаграмма линейных ЭДС (б).

3. Определить:

а) массы стали стержней и ярм, потери холостого хода Рх, среднее значение тока холостого хода i₀ и его активной составляющей i_0а и реактивной i_0p составляющих, а также cosφ₀ - все величины для номинального значения напряжения Uном при частоте f=50 Гц. Плотность холоднокатаной стали .

Объем стержня и ярма:

Масса стали стержня и ярма:

Общая масса стали стержней и ярм:

Потери холостого хода:

где К_П=1,8 - коэффициент учитывающий добавочные потери, возникающие вследствие несовпадения направления вектора магнитной индукции с направлением прокатки стали.

Электромагнитная индукция с стержне и ярме:

Для известных значений индукции и марки стали 3404 в сердечниках и ярмах имеем удельные потери р и удельные намагничивающие мощности q.

По таблице 8.10 (2) определяются:

- удельные потери в стержне: ;

- удельные потери в ярме: .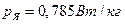

Общая намагничивающая мощность магнитной системы:

где К_Т - коэффициент, учитывающий увеличение намагничивающей мощности, который принимается Кт =10.

По таблице 8.17 (2) определяются:

- удельные намагничивающие мощности в стержне: ;

- удельные намагничивающие мощности в стержне: .

Активная составляющая тока ХХ:

Реактивная составляющая тока ХХ:

Полный ток XX:

Реальный ток XX.

Активная составляющая тока ХХ:

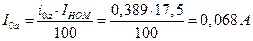
Реактивная составляющая тока ХХ:

Полный ток XX:

 

Коэффициент мощности:

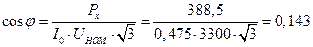
Погрешность расчета потерь XX трансформатора:

Погрешность расчета тока XX трансформатора:

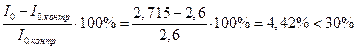
б) параметры схемы замещения г₀ и х₀ и z₀ в омах при U= U_H0M, приведенные к первичной обмотке.

Рисунок 3 – Схема замещения трансформатора в режиме ХХ.

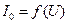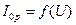в) рассчитывается и строится характеристика холостого хода: ; и , а также графики и для диапазона значений U от 50 до 110% от U_НОМ.

U, В	0,5UВН	0,7UВН	0,9UВН	1,0UВН	1,1UВН
Bc, Тл	0,8	1,1	1,42	1,57	1,73
Bя, Тл	0,66	0,92	1,18	1,31	1,45
рс, Вт/кг	0,32	0,475	0,964	1,207	1,672
ря, Вт/кг	0,19	0,675	0,697	0,785	0,998
qс, ВА/кг	0,375	0,782	1,114	1,575	5,56
qя, ВА/кг	0,234	0,752	0,811	0,932	1,168
Рх, Вт	99,605	221,98	323,57	388,5	521,4
Qх, ВА	660,36	1653,8	2083,1	2686,7	7379,0
i0a, %	0,0996	0,222	0,3236	0,389	0,5214
i0р, %	0,6604	1,6538	2,0831	2,687	2,7203
i0, %	0,6678	1,6686	2,1081	2,715	7,3974
cosφ0	0,522	0,3325	0,2984	0,143	0,112

 

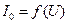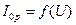Таблица 1 – Данные вычислений характеристик холостого хода: ; и , а также графиков и для диапазона значений U от 50 до 110% от U_НОМ.

Рисунок 4 - Графики зависимосте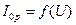й , и .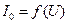

 

Рисунок 5 - Графики зависимостей и .

 

г) потери ХХ трансформатора, при включении в сеть с частотой 40 и 60Гц.

Для известных значений индукции и марки стали 3404 в сердечниках и ярмах имеем удельные потери р и удельные намагничивающие мощности q. По таблице 8.10 (2) определяются:

- удельные потери в стержне: ;

- удельные потери в ярме: ; .

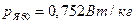4. Определить:

а) Потери КЗ Рк.

Плотность металла обмоток алюминия .

Масса металла каждой из обмоток находится по формуле:

где с — число активных стержней;

Dcp - средний диаметр обмотки;

w — число витков обмотки;

S - сечение витка.

Средний диаметр:

- обмотки ВН:

- обмотки НН:

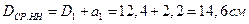
Массы обмоток ВН и НН:

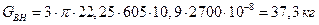
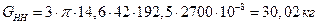
Основные потери в обмотках:

где J - плотность тока в обмотке.

Плотность тока в обмотках ВН и НН:

;

Потери короткого замыкания:

Находим потери при КЗ:

Погрешность расчета потерь КЗ:

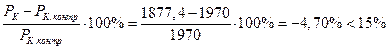
б) сопротивления короткого замыкания r_K, х_К, z_K в омах, приведенные к первичной обмотке; составляющие напряжения короткого замыкания u_а и u_р, напряжение короткого замыкания u_к в процентах и cosφ.

Активная составляющая напряжения короткого замыкания:

или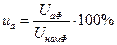

Реактивная составляющая напряжения короткого замыкания:

или

Сопротивление Z_K:

;

Активные составляющие:

;

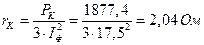
Коэффициент Роговского:

 

Реактивные составляющие:

Находим реактивные составляющие:

;

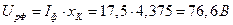Напряжение КЗ:

Погрешность расчетов напряжения КЗ:

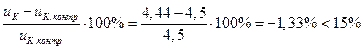
Сопротивление Z_K:

; ;

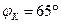
в) рассчитать и построить график изменения вторичного напряжения трансформатора Δu=f(cosφ₂) при номинальном токе.

Определить cosφ₂, при котором Δu принимает максимально значение. Построить на одной диаграмме внешнюю характеристику U2=f(I₂) и график Δu =f(I₂) при cosφ₂=1 и cosφ₂=0,7.

;

	1,874	3,270	3,633	4,168	4,4193	4,436	4,432	4,285	4,021

Таблица 2 – Расчет зависимости Δu=f(cosφ₂).

Рисунок 6 - График изменения вторичного напряжения

трансформатора Δu=f(cosφ₂).

Зависимость U₂=f(I₂) и график Δu =f(I₂) при cosφ₂=1 и cosφ₂=0,7.

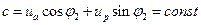
при ;

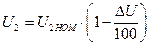
при и cosφ2=0,7, RL-нагрузка
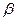
	0,2	0,4	0,6	0,8	1,0
	0,833	1,667	2,50	3,333	4,167
	228,083	226,167	224,25	222,333	220,417
	50,2	100,4	150,6	200,8	251,0

Таблица 3 – Расчет зависимости при и cosφ₂=0,7,

активно-индуктивная нагрузка.

при и cosφ2=1, активная нагрузка.
	0,2	0,4	0,6	0,8	1,0
	0,375	0,75	1,124	1,499	1,874
	229,138	228,276	227,414	226,552	225,69
	50,2	100,4	150,6	200,8	251,0

Таблица 4 – Расчет зависимости при и cosφ₂=1

активная нагрузка.

при и cosφ2=0,7, RС-нагрузка
	0,2	0,4	0,6	0,8	1,0
	-0,309	-0,617	-0,926	-1,234	-1,543
	230,71	231,42	232,129	232,839	233,549
	50,2	100,4	150,6	200,8	251,0

Таблица 5 – Расчет зависимости при и cosφ₂=1

активно-емкостная нагрузка.

По рассчитанным данным строятся зависимости при различных нагрузках, в одних координатных осях.

Рисунок 7 - Зависимости при различных нагрузках.

 

5. Построить в масштабе приведенную векторную диаграмму для одной фазы трансформатора при нагрузке номинальным током и cosφ₂=0,8.

Так как при приведении вторичной обмотки трансформатора к первичной принимается допущение, то, приведенная вторичная обмотка устроена совершенно так же как первичная, поэтому можно считать, что и сопротивления их равны.

Рисунок 8 – Схема замещения трансформатора.

Таким образом:

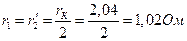
Приведенный вторичный ток:

Рисунок 9 - Векторная диаграмма трансформатора при активно-индуктивной нагрузке (сosφ = 0,8).

 

Приведенное вторичное напряжение:

Падение напряжения в активном сопротивлении вторичной обмотки , приведенное к первичной цепи:

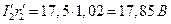
Падение напряжения в индуктивном сопротивлении вторичной обмотки 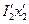, приведенное к первичной цепи;

Падение напряжения в активном сопротивлении первичной обмотки :

Падение напряжения в индуктивном сопротивлении первичной обмотки :

 

6. Рассчитать и построить зависимость КПД от нагрузки η=f(P2) при cosφ₂=1 и cosφ₂=0,7. Определить P₂, при котором η приобретает максимальное значение.

; при

; при

 

 

.

 

 

 

Рисунок 10 - Зависимость КПД от нагрузки η=f(P2)

при cosφ₂=1 и cosφ₂=0,7.

 

Список литературы.

1. В.Б. Баль, С.И. Копылов, М.В. Панихин. РАСЧЕТ ТРАНСФОРМАТОРОВ. Учебное пособие по курсам «Электрические машины», «Проектирование электрических машин», для студентов, обучающихся по направлению «Электротехника и электроэнергетика». Москва., Издательство МЭИ., 2016.,

2. Тихомиров П.М. Расчет трансформаторов. М., "ЭНЕРГОАТОМИЗДАТ", 1986. – 528 с.:ил.

3. Сапожников А.В. Конструирование трансформаторов. К., Госэнергоиздат, 1959.

4. Сапожников А.В. Силовые трансформаторы /учебные таблицы/, М., Госэнергоиздат, 1955.