Глава 37. Параметры. Линейные методы.
A. Теорема Виета. Теорема Безу.
№У37.2) Если многочлен 
можно представить в виде 
, то сумма 
равна…
№У37.3) Известно, что один из корней уравнения 
равен 
. Найдите все возможные значения 
.
№37.4) Известно, что один из корней уравнения 
равен 
. Найдите все возможные значения 
.
№С37.5) Известно, что один из корней уравнения 
равен 
. Найдите все возможные значения .
№37.6) Известно, что один из корней уравнения 
равен 
. Найдите все возможные значения .
№У37.7) Числа 
и таковы, что система 
имеет единственное решение х=1, у=1. Найти числа и .
Ответы к главе 37.
№37.2) 4; №37.3) -8; -3; №37.4) -5; 0,5; №37.5) -8; -2,5; №37.6) -10; -4; №37.7) 
;
B. ОДЗ.
№У37.8) Квадратное уравнение, корни которого на одну единицу меньше корней уравнения 
, имеет вид 
. Найдите 
.
№У37.9) Решить уравнение с параметром: 
.
№С37.10) Решить уравнение с параметром: 
.
№У37.11) Решить уравнение с параметром: 
.
№37.12) Решить уравнение с параметром: 
.
№У37.13) Решить уравнение с параметром: 
.
№С37.14) Решить уравнение с параметром: 
.
№С37.15) Решить уравнение с параметром: 
.
№С37.16) Решить уравнение с параметром: 
.
№У37.17) Решить уравнение с параметром: 
.
№У37.19) Найдите наименьшее целое значение , при котором абсцисса всех общих точек графиков функций 
и 
отрицательна.
№У37.20) При каком значении уравнение 
имеет одно решение.
№С37.21) При каком значении уравнение 
не имеет решения?
№У37.22) Числа , и таковы, что система 
имеет бесконечно много решений, причем х=1, у=3 одно из этих решений. Найти числа , и .
Ответы к главе 37.
№37.8) -8; №37.9) 
; №37.10) 
; №37.11) 
; №37.12) 
; №37.13) 
; №37.14) 
; №37.15) 
;
№37.16) 
; №37.17)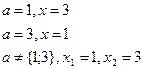 
;
№37.19) 
; №37.20) 
; №37.21) 
; №37.22) 
.
C. Замена переменной.
№У37.23) Определить все действительные значения параметра , при каждом из которых уравнение 
имеет решения и найти все эти решения.
№С37.24) Определить все действительные значения параметра , при каждом из которых уравнение 
имеет решения и найти все эти решения.
Ответы к главе 37.
№37.23) 
, 
; №37.24) 
, 
;
Глава 38. Параметры. Использование свойств функций.
B
№У38.1) При каких значениях параметра область определения функции 
совпадает с множеством всех действительных чисел?
№С38.2) При каких значениях параметра область определения функции 
совпадает с множеством всех действительных чисел?
№У38.3) Найти все значения параметра , при каждом из которых система неравенств 
имеет единственное решение.
Ответы к главе 38.
№38.1) 
; №38.2) 
; №38.3) 
.
C
№У38.4) Определите, при каких отрицательных значениях параметра в решении неравенства 
содержатся все натуральные числа?
№У38.5) Найдите все значения параметра , при которых уравнение 
имеет ровно два корня на отрезке 
.
№У38.6) При каких значениях параметра уравнение 
имеет единственное решение? В ответе запишите наименьшее целое значение параметра .
№У38.7) Найдите все значения параметра , при которых неравенство 
выполняется для всех 
, таких, что 
.
№У38.8) Найдите все значения , при которых неравенство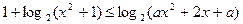 
выполняется для любого значения .
№У38.9) Найдите все положительные значения , для каждого из которых неравенство 
выполняется для любого .
№У38.10) Найти все значения параметра , при каждом из которых один из корней уравнения 
меньше, чем -2, а второй корень не меньше, чем 1.
№С38.11) Найти все значения параметра , при каждом из которых один из корней уравнения 
меньше, чем -1, а второй корень не меньше, чем 3.
№У38.12) При каких значениях параметра уравнение 
имеет более одного решения?
№У38.13) При каких значениях параметра уравнение 
имеет только целые корни?
Ответы к главе 38.
№38.4) 
; №38.5) 
; №38.6) 
; №38.7)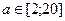 
; №38.8) 
; №38.9) 
; №38.10) 
; №38.11) 
; №38.12) 
; №38.13) 
.
D
№У38.14) Найти все значения , при каждом из которых уравнение 
имеет корни как большие -3, так и меньшие -3.
№У38.15) Найдите все значения параметра , при каждом из которых множество решений неравенства 
содержит хотя бы одно целое число.
№У38.16) Найдите все неотрицательные значения параметра , при каждом из которых неравенство 
выполняется для всех значений .
Ответы к главе 38.
№38.14) 
; №38.15) 
; №38.16) 
.