Справочные материалы к экзамену по математике за 2 семестр
| Определения степени | Свойства степеней | |
 (n множителей) (n множителей)
| 1. 
| 6. Если 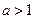 и и  , то , то 
|
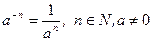
| 2. 
| 7. Если  и и  , то , то  . .
|
 . . 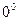 не определено не определено
| 3. 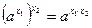
| 8. Если  и и 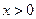 , то , то 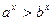 . .
|
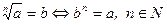
| 4. 
| 9. Если  и и 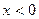 , то , то  . .
|

| 5. 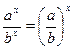
| 10. Если  то то 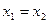 . .
|
Значения степени 
| n a | ||||||||||
Логарифмы
Определение логарифма. Пусть 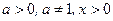 .
. 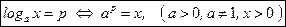
Замечание.  – десятичный логарифм x;
– десятичный логарифм x;  – натуральный логарифм x.
– натуральный логарифм x.
 ,
,  .
.
Свойства логарифмов
1. 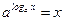
| 3. 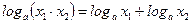
| 5. 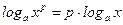
| 7. 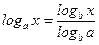
|
2. 
| 4. 
| 6. 
| 8. 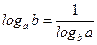
|
Табличные значения тригонометрических функций
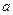
| 
| 
| 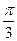
| 
| 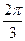
| 
| 
| 
| |

| 
| 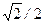
| 
| 
| 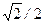
| 
| |||

| 
| 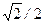
| 
| 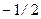
| 
| 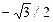
| 
| ||
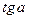
| 
| 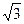
| Не опр. | 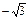
| 
| 
| |||
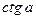
| Не опр. | 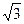
| 
| 
| 
| 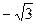
| Не опр. |
Табличные значения обратных тригонометрических функций
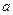
| 
| 
| 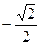
| 
| 
| 
| 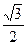
| 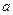
| 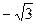
| 
| 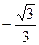
| 
| 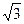
| |||||
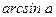
| 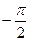
| 
| 
| 
| 
| 
| 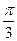
| 
| 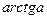
| 
| 
| 
| 
| 
| 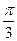
| |||

| 
| 
| 
| 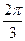
| 
| 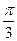
| 
| 
| 
| 
| 
| 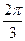
| 
| 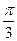
| 
| 
|
Формулы корней тригонометрических уравнений
| Общие формулы | ||
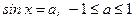  
  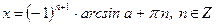
| ||
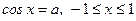  
| ||
  
| ||
   или или 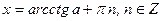
| ||
| Частные формулы | ||
  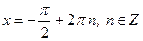
|   
|   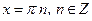
|
  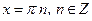
| 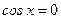  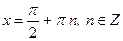
| 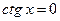 
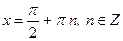
|
  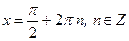
|   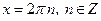
|
Производные и первообразные некоторых элементарных функций
Данная функция 
| Производная 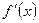
| Первообразная

| Данная функция 
| Производная 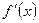
| Первообразная

| |

| 
| 
| 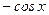
| |||
 , ,

| 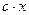
| 
| 
| 
| ||
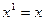
| 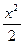
| 
| 
| 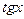
| ||
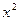
| 
| 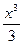
| 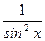
| 
| 
| |

| 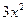
| 
| 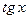
| 
| 
| |
 , , 
| 
| 
| 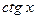
| 
| 
| |

| 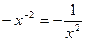
| 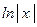
| 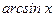
| 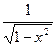
| 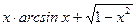
| |
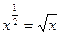
| 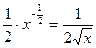
| 
| 
| 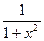
| 
| |

| 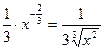
| 
| 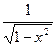
| 
| 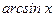
| |
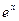
| 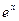
| 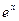
| 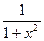
| 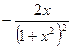
| 
| |
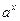 , ,
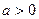 , , 
| 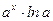
| 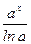
| 
| 
| 
| |

| 
| 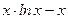
| 
| 
| 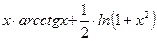
|
Площади поверхностей и объемы геометрических тел


Правильные многогранники
| Тип правильного многогранника | Количество и тип граней | Площадь поверхности | Объем | Радиус вписанной сферы | Радиус описанной сферы |
Правильный тетраэдр

| правильных треугольника | 
| 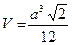
| 
| 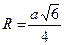
|
Правильный октаэдр

| правильных треугольников | 
| 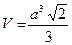
| 
| 
|
Правильный икосаэдр

| правильных треугольников | 
| 
| 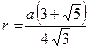
| 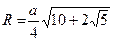
|
Правильный гексаэдр

| квадратов | 
| 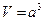
| 
| 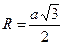
|
Правильный додекаэдр

| правильных пяти-угольников | 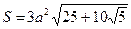
| 
| 
| 
|
Формулы для вычисления площадей некоторых фигур
1. Площадь треугольника можно найти по следующим формулам:
 ;
;  ;
;
 , где
, где  .
.
2. Площадь правильного (равностороннего) треугольника со стороной 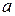 можно найти по формуле
можно найти по формуле  .
.
3. Площадь параллелограмма равна произведению его основания на высоту:  . Площадь параллелограмма со сторонами a и b и углом
. Площадь параллелограмма со сторонами a и b и углом  между ними можно найти по формуле:
между ними можно найти по формуле: 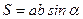 .
.
4. Площадь ромба равна половине произведения его диагоналей: 
5. Площадь трапеции с основаниями a и b и высотой h можно найти по формуле 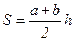 .
.
6. Площадь правильного n- угольника со стороной a можно найти по формуле 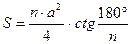 .
.
7. Площадь любого n- угольника можно найти, разбив его диагоналями на треугольники и вычислив площадь каждого треугольника по подходящей формуле.
8. Площадь круга радиуса  вычисляется по формуле
вычисляется по формуле 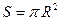 ,
,
длина окружности радиуса  вычисляется по формуле
вычисляется по формуле 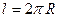 .
.
Метрические соотношения в прямоугольном треугольнике
 Синусом острого у гла в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе:
Синусом острого у гла в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе: 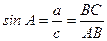
Косинусом острого у гла в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе: 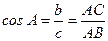
Тангенсом острого у гла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему: 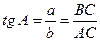 .
.
Котангенсом острого у гла в прямоугольном треугольнике называется отношение прилежащего катета к противолежащему: 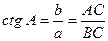 .
.
Сумма острых углов прямоугольного треугольника равна 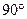 :
:  .
.
Если  – высота треугольника, проведенная к гипотенузе, то площадь треугольника
– высота треугольника, проведенная к гипотенузе, то площадь треугольника  и
и 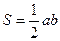 , откуда
, откуда 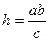 .
.
Так как треугольники ABC, ACD и CBD попарно подобны, то справедливы соотношения: 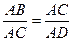 ,
,  ,
, 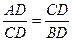 .
.
Метрические соотношения в произвольном треугольнике
Теорема синусов. Длины сторон треугольника пропорциональны синусам противоположных углов:  , где
, где  – радиус окружности, описанной около треугольника.
– радиус окружности, описанной около треугольника.
Теорема косинусов: квадрат стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними: 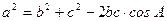 ,
, 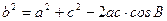 ,
,  .
.
Если a, b, c – длины сторон треугольника, S – его площадь, то радиус окружности, описанной около треугольника, можно вычислить по формуле  , а радиус окружности, вписанной в треугольник, по формуле
, а радиус окружности, вписанной в треугольник, по формуле  .
.