Интервальное оценивание
Доверительным интервалом для параметра q называется интервал 
, накрывающий истинное значение q с заданной вероятностью g = 1 - a, то есть
.
Число g = 1 - a называется доверительной вероятностью, а значение a - уровнем значимости. Статистики 
и 
,определяемые по выборке 
из генеральной совокупности с неизвестным параметром q, называются нижней и верхней границами доверительного интервала (или левой и правой границами).
Чтобы найти доверительный интервал для параметра q, необходимо знать закон распределения статистики 
, значение которой является оценкой параметра q.
Один из методов построения доверительного интервала состоит в следующем. Пусть существует статистика 
такая, что:
а) закон распределения Y известен и не зависит от q,
б) функция 
непрерывна и строго монотонна по q.
Пусть g = 1 - a - заданная доверительная вероятность, а 
и 
- квантили статистики Y порядков 
и 
соответственно. Тогда с вероятностью g = 1 - a выполняется неравенство:
.
Решая неравенство относительно q, найдем границы 
и 
доверительного интервала для q.
Распределение некоторых статистик
Для основных статистик, вычисляемых на основе выборки объема n из нормально распределенной 
генеральной совокупности имеют место следующие результаты.
1. Выборочное среднее 
имеет нормальное распределение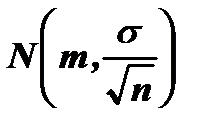 
.
2. Выборочная дисперсия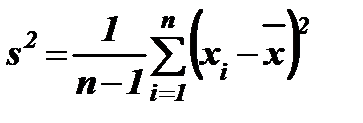 
связана со случайной величиной 
соотношением:
.
3. Статистика 
является случайной величиной, имеющей распределение Стьюдента с (n – 1) степенью свободы Т (n – 1).
4. Пусть 
и 
- выборочные дисперсии, вычисленные по независимым выборкам объема n1 и n1 из двух нормально распределенных генеральных совокупностей с дисперсиями 
и 
, тогда отношение 
имеет распределение Фишера с (n1 – 1) и (n2 – 1) степенями свободы 
.
Доверительный интервал для среднего
Пусть 
- выборка n наблюдений случайной величины X ~ N (m,s). В качестве оценки математического ожидания m возьмем выборочное среднее 
.
1. Пусть дисперсия генеральной совокупности 
известна. Рассмотрим статистику 
~ N (0,1). Найдем квантили 
и 
стандартного нормального распределения N (0,1). Вероятность события 
будет равна заданной доверительной вероятности g = 1 - a, то есть 
.
Решая неравенство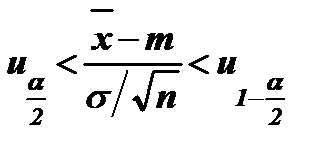 
относительно m, получим, что с вероятностью g выполняется условие 
. Учитывая, что для квантилей стандартного (нормированного) нормального распределения 
= - 
, доверительный интервал для математического ожидания m примет вид:
.
2. Пусть дисперсия генеральной совокупности неизвестна. Тогда по выборке наблюдений определим оценку дисперсии 
. Доверительный интервал для среднего в этом случае находят, используя статистику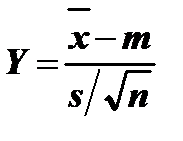 
~ Т (n-1), имеющую распределение Стьюдента с n – 1 степенью свободы. По заданной доверительной вероятности g = 1 - a находим квантили 
и 
распределения Стьюдента с (n-1) степенью свободы. Решая неравенство 
относительно m и используя соотношение для квантилей Стьюдента
= - 
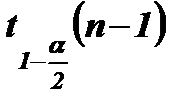, получим, что доверительный интервал для среднего при неизвестной дисперсии равен
.
Доверительный интервал для дисперсии
Пусть среднее генеральной совокупности неизвестно. В качестве оценки дисперсии используют выборочную дисперсию 
. Статистика 
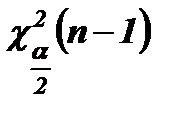имеет распределение c2 (n-1). Определим квантили 
и 
, удовлетворяющие условию 
.
Решая неравенство 
относительно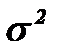 
, получим доверительный интервал для дисперсии:
.