Численное интегрирование
Отрезок (a,b) разобьем на ряд под отрезков:  . Тогда
. Тогда  по всем i. По нескольким точкам можно построить интерполяционный многочлен не высокой степени.
по всем i. По нескольким точкам можно построить интерполяционный многочлен не высокой степени.
Выбирая j=i+1, i+2 получают интерполяционные многочлены 2-й степени, которые позволяют получить значение интеграла с удовлетворительной для практических целей точностью.
Формулы прямоугольников
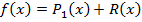
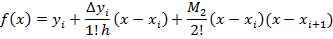
Для упрощения в методе прямоугольников. На единичном отрезке строится интерполяционный многочлен нулевой степени, т е 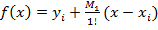 тогда
тогда  , Q-погрешность численного интегрирования
, Q-погрешность численного интегрирования 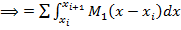 или
или 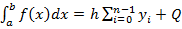 -(1)ф-ла левых прямоугольников.
-(1)ф-ла левых прямоугольников.  -(2)ф-ла правых.
-(2)ф-ла правых.
1) Под интегральную ф-ю необход затабулировать.
2) Если в интерполяционном многочлене использовать 2-ю ф-лу Ньютона, то будет получена ф-ла правых прямоугольников. При этом погрешность нахождения интеграла Q не превосходит величины  , n-число отрезков.
, n-число отрезков.
Формула погрешности позволяет решить не только прямую задачу ЧИ но и обратную.
Прямая задача: вычислить опред-й интеграл и оценить погрешность найденного значения.
Обратная задача: вычислить значение интеграла с точностью не превосходящей Q.
Формула трапеций
Используя на единичном отрезке интерполяционный многочлен 1-й степени
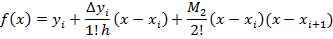
Можно получить соотношение: 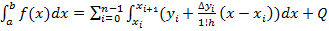
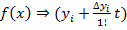 то
то 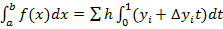
 (по определению). Вычисление дает след ф-лу трапеций:
(по определению). Вычисление дает след ф-лу трапеций: 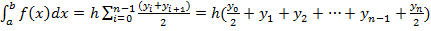 . Оценка погрешности дает:
. Оценка погрешности дает: 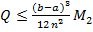 . Ф-ла трапеций дает значение равное среднему арифметическому значений полученных по ф-ам левых и правых прямоугольников.
. Ф-ла трапеций дает значение равное среднему арифметическому значений полученных по ф-ам левых и правых прямоугольников.
Формула сипсона.
Интервал интегрирования (a,b) разбивается на четное число под интервалов. 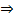 необходимо рассмотреть под интервалы состоящие из 3-х точек:
необходимо рассмотреть под интервалы состоящие из 3-х точек: 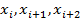 .
.



n -число двойных интегралов.
| x | f(x) |
a= 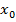
| 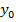
|

| 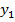
|
Формула симпсона в большинстве практических задач обеспечивает удовлетвор точность нахождения интеграла. При необходимости с помощью рассмотренного выше алгоритма можно найти ф-лы более и более высокой точности.
Численное решение дифур.
Обыкновенные дыфуры 1-го порядка.
Пусть диф ур-е вырожено в явном виде: 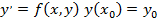 .
.
Найти 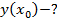 , где х-произвол точка.
, где х-произвол точка.
-аналитическое решение;
-приближенное(численное и графическое).
интервал (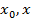 ) разбиваем на ряд под интегралов:
) разбиваем на ряд под интегралов: 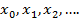 Затем производную заменяем конечно разностным отношением:
Затем производную заменяем конечно разностным отношением:  при этом ф-ю f(x,y)-заменяем значением ф-ии в узлах(дискретизация).
при этом ф-ю f(x,y)-заменяем значением ф-ии в узлах(дискретизация). 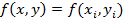 . Тогда
. Тогда 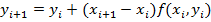 . На практике чаще всего используется равномерная дискретизация тогда получаем ф-лу Эйлера:
. На практике чаще всего используется равномерная дискретизация тогда получаем ф-лу Эйлера: 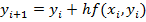 .
.
Метод Эйлера обладает очень низкой точностью, и иначе наз методом касательных.
Предположим что знаем точное значение y(x). Рассмотрим точку  . Значит
. Значит  -точное.
-точное.
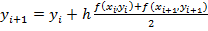 .(1). Если рассматривать как вектора, то получим min погрешность. Полученная рекуррентная ф-ла явл не явной, т к искомая величина
.(1). Если рассматривать как вектора, то получим min погрешность. Полученная рекуррентная ф-ла явл не явной, т к искомая величина  находится и в левом и в правом соотношении. Для нахождения
находится и в левом и в правом соотношении. Для нахождения  необходимо решить нелинейное уравнение относительно
необходимо решить нелинейное уравнение относительно  . Т к в общем случае задача оказывается достаточно сложной. Эйлер предложил решать задачу в два этапа:
. Т к в общем случае задача оказывается достаточно сложной. Эйлер предложил решать задачу в два этапа:
I этап: по обычной схеме Эйлера находится приближенное значение:  . Затем производится уточнение найденного значения по ф-ле (1), где вместо
. Затем производится уточнение найденного значения по ф-ле (1), где вместо 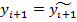 .
.
II этап: подставляем в 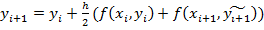 .
.
Рунгк и кутта предложили: 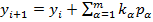 ,
,  -значение f(x,y) в точке
-значение f(x,y) в точке 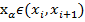 .
.  -нормировочные коэф-ы значения которых подбираются. Значения
-нормировочные коэф-ы значения которых подбираются. Значения  можно найти в виде разложения ф-й f(x,y) в ряд Тейлора в близи точки
можно найти в виде разложения ф-й f(x,y) в ряд Тейлора в близи точки  и сравнение полученного разложения с разложением в ряд ф-ии y(x).
и сравнение полученного разложения с разложением в ряд ф-ии y(x).
Число точек m наз порядком схемы Рунге-кутты.
Для m=1, расчетная ф-а приобретает вид: 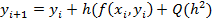 при этом показывается что на каждом шаге будет допускаться погрешность метода порядка
при этом показывается что на каждом шаге будет допускаться погрешность метода порядка 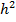 .
.
Поскольку полное решение задачи потребует n-шагов (n 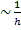 ), то полная погрешность будет иметь порядок h.
), то полная погрешность будет иметь порядок h. 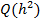 - оценочная погрешность метода.
- оценочная погрешность метода.
m=2: 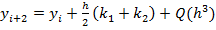 , где
, где 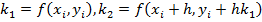 . Схема Рунге-Кутты 2-го порядка эквивалентна методу Эйлера с пересчетом.
. Схема Рунге-Кутты 2-го порядка эквивалентна методу Эйлера с пересчетом.
На практике наиболее часто используют схему Рунге-Кутты 4-го порядка, т е m=4: 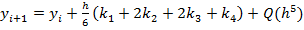 ,
,  ,
,  ,
, 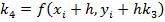 .
.
Для оценки общей погрешности решения задачи, можно использовать правила Рунге:  . Погрешность интегр-я ОДУ = отношению модуля разности решений в заданной точке полученных с шагом h и h/2, к (
. Погрешность интегр-я ОДУ = отношению модуля разности решений в заданной точке полученных с шагом h и h/2, к (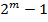 ), где m-это порядок используемой схемы Рунге-Кутты.
), где m-это порядок используемой схемы Рунге-Кутты.
Это же ф-ла может использоваться и для определения погрешности нахождения интеграла.
Метод Пикара.
Пусть дано диф ур-е: 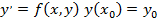 . Пикар записал его в виде:
. Пикар записал его в виде: 
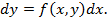 Затем данное ур-е интегрируется:
Затем данное ур-е интегрируется:  . Полученная ф-ла явл неявным отношением искомой ф-ии y. Пикар предложил использовать интерационную схему последовательного уточнения искомой ф-ии y(x).
. Полученная ф-ла явл неявным отношением искомой ф-ии y. Пикар предложил использовать интерационную схему последовательного уточнения искомой ф-ии y(x).
 при этом
при этом 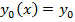
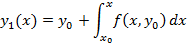
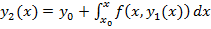 . Повторив данную процедуру большое число раз, можно определить функциональную зависимость y(x). Оценка погрешности найденного решения может быть найдена по теореме Пикара.
. Повторив данную процедуру большое число раз, можно определить функциональную зависимость y(x). Оценка погрешности найденного решения может быть найдена по теореме Пикара.