Геометрическое представление комплексных чисел

Уже в XVI столетии в математических работах появляются квадратные корни из отрицательных чисел в формулах, дающих решения квадратных уравнений. Но в те времена математики затруднились бы объяснить точный смысл этих выражений, к которым относились почти с суеверным трепетом. Сам термин "мнимый" до сих пор напоминает нам о том, что эти выражения рассматривались как нечто искусственное, лишенное реального значения. И только в начале XIX в., когда уже выяснилась роль комплексных чисел в различных областях математики, было дано очень простое геометрическое истолкование комплексных чисел и операций с ними, и этим был положен конец сомнениям в возможности их законного употребления. Конечно, с современной точки зрения формальные операции с комплексными числами полностью оправдываются на основе формальных определений, так что геометрическое представление логически не является необходимым. Но такое представление, предложенное почти одновременно Весселем (1745- 1818), Арганом (1768-1822) и Гауссом, позволило рассматривать комплексные числа и действия с ними как нечто вполне естественное с интуитивной точки зрения и, кроме того, имеющее чрезвычайно большое значение в приложениях комплексных чисел как в самой математике, так и в математической физике.

Геометрическая интерпретация комплексных чисел заключается в том, что комплексному числу z = х + yi сопоставляется точка на плоскости с координатами х, у. Именно действительная часть числа мыслится как х-координата, а мнимая - как y-координата. Таким образом устанавливается взаимно однозначное соответствие между комплексными числами и точками "числовой плоскости", подобно тому как нами было установлено раньше (см. § 2) соответствие между действительными числами и точками "числовой оси". Точкам на оси х в числовой плоскости соответствуют действительные числа х = x + 0i, а точкам на оси у - чисто мнимые числа z = 0 + yi. Если

z = х + yi

есть какое-то комплексное число, то число

z = х - yi

мы называем сопряженным с числом z. В числовой плоскости точка 7 получается из точки z посредством зеркального отражения относительно оси х. Если мы условимся расстояние точки z от начала обозначать через р, то на основании теоремы Пифагора

р² = x² + у² = (x + yi)(x - yi) = z*z.

Действительное число 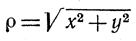называется модулем z и обозначается

ρ = |z|.

Если z лежит на действительной оси, то модуль совпадает с абсолютной величиной z. Комплексные числа с модулем 1 изображаются точками, лежащими на "единичной окружности" с центром в начале и радиусом 1.

Если |z| = 0, то z = 0. Это следует из определения |z| как расстояния точки z от начала. Далее, модуль произведения двух комплексных чисел равен произведению модулей

|z₁*z₂| = |z₁|*|z₂|.

Это вытекает как следствие из более общей теоремы, которая будет доказана на стр. 124.

Упражнения. 1) Доказать последнюю теорему, исходя непосредственно из определения умножения двух комплексных чисел z₁ = х₁ + у₁i и z₂ = х₂ + у₂i

2) Пользуясь тем обстоятельством, что произведение двух действительных чисел равно нулю в том и только в том случае, если один из множителей равен нулю, доказать соответствующую теорему для комплексных чисел. (Указание. Основывайтесь при доказательстве на двух последних теоремах.)

Согласно определению сложения двух комплексных чисел z₁ = x₁ + y₁i и z₂ = х₂ + y₂i мы имеем:

z₁ + z₂ = (x₁ + x₂) + (y₁ + y₂)i.

Таким образом, точка z₁ + z₂ изображается в числовой плоскости четвертой вершиной параллелограмма, у которого тремя первыми вершинами являются точки 0, z₁, z₂. Этот простой способ построения суммы двух комплексных чисел ведет ко многим важным следствиям. Из него мы заключаем, что модуль суммы двух комплексных чисел не превышает суммы модулей (ср. стр. 83):

|z₁ + z₂|≤|z₁| + |z₂|.

Достаточно сослаться на то, что длина стороны треугольника не превышает суммы длин двух других сторон.

Упражнение. В каких случаях имеет место равенство |z₁ + z₂| = |z₁| + |z₂|?

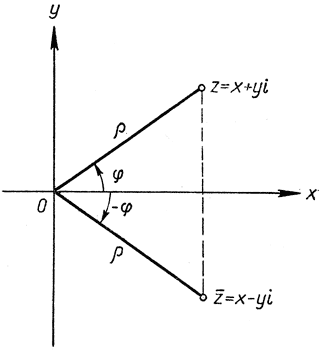
Рис. 22. Геометрическое представление комплексных чисел. Точка z имеет прямоугольные координаты х, y

Угол между положительным направлением оси х и отрезком Oz называется аргументом z и обозначается буквой φ (см. рис. 22). Числа 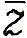и z имеют один и тот же модуль

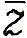| | = |z|,

но их аргументы противоположны по знаку:

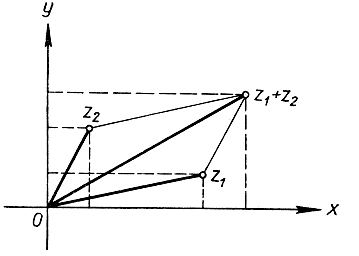
Рис. 23. Сложение комплексных чисел по правилу параллелограмма

Конечно, аргумент z определяется не однозначно, так как к нему можно прибавлять или из него вычитать любой угол, кратный 360°, не изменяя направления отрезка Oz. Итак, углы

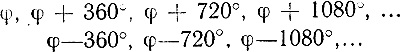
графически дают один и тот же аргумент.

Так как, согласно определению синуса и косинуса,

х = ρcosφ, y = ρsinφ,

то любое комплексное число z выражается через его модуль и аргумент следующим образом:

z = х + yi = ρ (соs φ + i sinφ). (8)

Например,

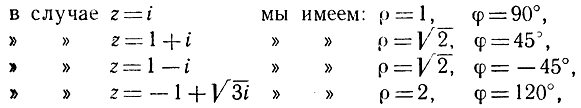
так что

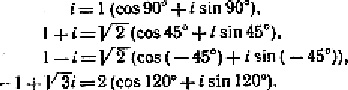
Читатель может проверить эти утверждения посредством подстановки числовых значений тригонометрических функций.

Тригонометрическим представлением (8) очень полезно воспользоваться, чтобы уяснить себе геометрический смысл умножения двух комплексных чисел. Если

z = ρ (cos φ + i sin φ)

и

z' = ρ' (cos φ' + i sin φ'),

то zz' = ρρ' {(cos φ cos φ' - sin φ - sin φ') + (cos φ sin φ' + sin φ соs φ')i}.

Нов силу основных теорем сложения для синуса и косинуса

cos φ cos φ' - sin φ sin φ' = cos' (φ + φ'),

cos φ sin φ' + sin φ соs φ' = sin (φ + φ').

Итак,

zz' = ρρ' {cos (φ + φ') + sin (φ + φ'}. (9)

В правой части последнего равенства мы видим написанное в тригонометрической форме комплексное число с модулем ρρ' и аргументом φ + φ'. Значит, мы можем отсюда заключить, что при умножении двух комплексных чисел их модули перемножаются, а аргументы складываются (рис. 24). Таким образом, мы видим, что умножение комплексных чисел как-то связано с вращением.

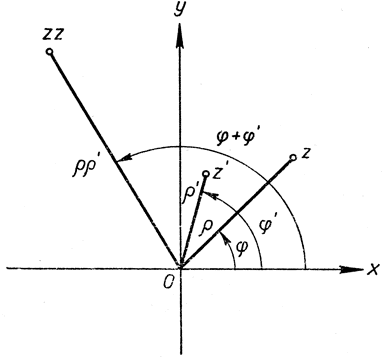
Рис. 24. Умножение комплексных чисел: аргументы складываются, модули перемножаются

Установим точнее, в чем тут дело. Назовем направленный отрезок, идущий из начала в точку z, вектором точки z; тогда модуль ρ = |z| есть его длина. Пусть z' - какая-нибудь точка единичной окружности, так что ρ' = 1. В таком случае умножение z на z' просто поворачивает вектор z на угол φ'. Если же ρ'&$8800;1, то, помимо вращения, длина вектора должна быть умножена на ρ'. Рекомендуем читателю самостоятельно проиллюстрировать эти факты, умножая различные комплексные числа на z₁ = i (вращение на 90°); z₂ = -i (то же вращение на 90°, но в обратном направлении); z₃ = 1 + i и z₄ = 1 - i.

Формула (9) в особенности представляет интерес, если z = z'; в этом случае имеем:

z² = ρ² (cis 2φ + i sin 2φ).

Умножая снова на z, будем иметь:

z³ = ρ³ (cos 3φ + i sin 3φ);

и, вообще, для любого z, повторяя операцию, получим:

zⁿ = ρⁿ (cos nφ + i sin nφ). (10)

В частности, если точка z находится на единичной окружности, так что ρ = 1, мы приходим к формуле, открытой французским математиком А. де-Муавром (1667-1754):

(соs φ + i sin φ)ⁿ = cos nφ + i sin nφ. (11)

Эта формула - одно из самых замечательных и полезных соотношений в элементарной математике. Поясним это примером. Возьмем n = 3 и разложим левую часть по формуле бинома

(u + v)³ = u³ + 3u²v + 3uv² + v³.

Тогда получим:

cos 3φ + i sin 3φ = cos³φ - 3 cos φ sin² φ + i (3 cos² φ sin φ - sin³ φ).

Одно такое комплексное равенство равносильно двум равенствам, связывающим действительные числа. В самом деле, если два комплексных числа равны, то в отдельности равны их действительные части и их мнимые части. Итак, можно написать

cos 3φ = cos³ φ - 3 cos φ sin² φ, sin 3φ = 3 cos² φ sin φ - sin³ φ.

Пользуясь затем соотношением

cos² φ + sin² φ = 1,

получим окончательно:

cos 3φ = cos³ φ - 3 cos φ (1 - cos² φ = 4 cos² φ - 3 cos φ.

sin 3φ = - 4 sin³ φ + 3sin φ.

Подобного рода формулы, выражающие sin nφ и cos nφ соответственно через sin φ и cos φ, легко получить при каком угодно целом значении n.

Упражнения.

1. Написать аналогичные формулы для sin 4φ и cos 4φ.

2. Предполагая, что точка z находится на единичной окружности, z = cos φ + i sin φ, показать, что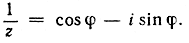

3. Без вычислении установить, что модуль числа 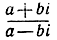равен единице.

4. Доказать: если z₁ и z₂ - два комплексных числа, то аргумент z₁ - z² равен углу между положительным направлением действительной оси и вектором, идущим от z₂ к z₁.

5. Дан треугольник с вершинами z₁, z₂, z₃; установить геометрический смысл аргумента числа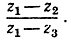

6. Доказать, что отношение двух комплексных чисел с одинаковым аргументом есть действительное число.

7. Доказать, что если аргументы чисел 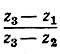и 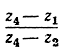равны между собой, то четыре точки z₁, z₂, z₃, z₄ лежат на окружности или на прямой линии, и обратно.

8. Доказать: четыре точки z₁, z₂, z₃, z₄ лежат на окружности или на прямой линии в том и только в том случае, если число

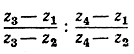
действительное.