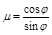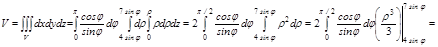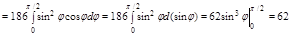Двойные интегралы
Вычисление двойных интегралов
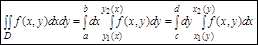
Задача. Вычислить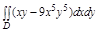 
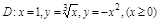
1. Область D правильная в направлении оси Oy в пределах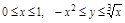 
2. 
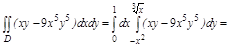
Замечание. Во внутреннем интеграле переменная, нестоящая под знаком дифференциала полагается константой
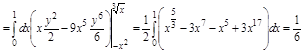
Задача. Вычислить двойной интеграл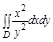 
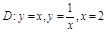
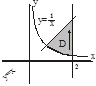1. Область D правильная в направлении Oy в пределах 
, 
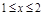2. 
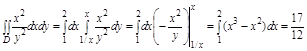
Задача. Вычислить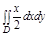 
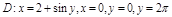
1. Область D правильная в направлении Oх в пределах 
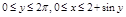
2. 
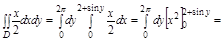
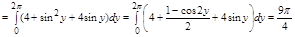
Изменение пределов интегрирования
Задача. Изменить порядок интегрирования в повторном интеграле.
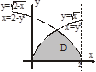
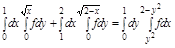
Задача. Изменить порядок интегрирования в повторном интеграле.
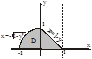
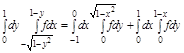
Задача. Изменить порядок интегрирования.
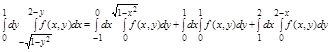
Вычисление площадей и объемов с помощью двойного интеграла
1. 
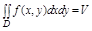цилиндра, ограниченного поверхностью z=f(x,y)
2. Если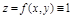 
, то 
области D
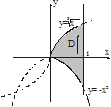
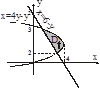Задача. Вычислить площадь плоской фигуры, ограниченной линиями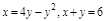 
1. Область D правильная в направлении Ох в пределах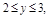 
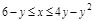
2. 
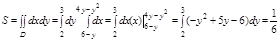
Задача. Найти площадь плоской фигуры, ограниченной линиями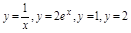 
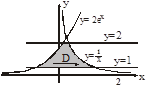1. Область D правильная в направлении Ох в пределах 
, 
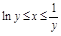
2. 
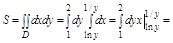
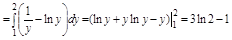
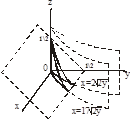Задача. Найти объём тела ограниченного поверхностями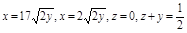 
1. Область D правильная в направлении Ох в пределах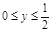 
, 
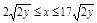
2. Цилиндр ограничен сверху поверхностью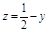 
, а снизу плоскостью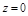 
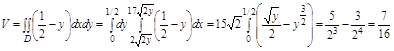
Задача. Найти объем тела, ограниченного поверхностями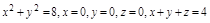 
1. Область D правильная во всех направлениях установим пределы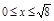 
, 
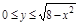
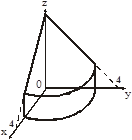2. Цилиндр ограничен сверху поверхностью 
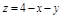, а снизу плоскостью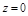
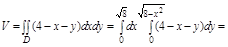
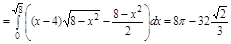
Замена переменных в двойном интеграл
Задача. Вычислить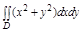 
, 
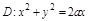
1. Перейдем в полярную систему координат
, 
, 
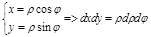
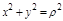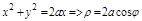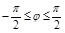
2. 
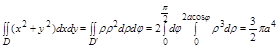
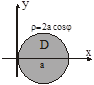
Задача. Вычислить площадь фигуры ограниченной линиями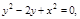 
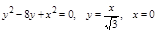
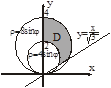Как и в предыдущем случае для достижения правильности области D нам придется рассекать её на три части.
|
|
Перейдем к полярной системе координат
, 
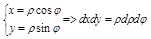
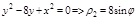
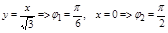
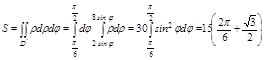
Тройной интеграл
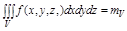
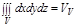
Задача. Вычислить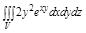 
, где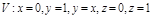 
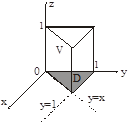1. Область V правильная в направлении оси Oz, а область D правильная во всех направлениях
Замечание. Если направление интегрирование области не имеет значения, надо выбрать то, которое упростит процесс непосредственного вычисление интегралов
а.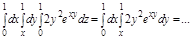 
б.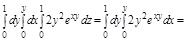 
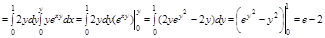
Задача. Вычислить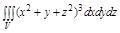 
, где 
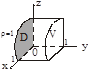1. Данная область V правильная в направлении оси Oz, поэтому спроектируем её в плоскость xOz
2. Перейдем в цилиндрическую систему координат
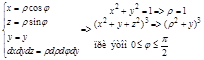
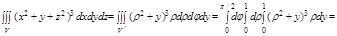
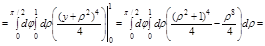
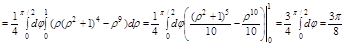
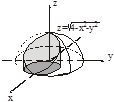Задача. Вычислить объем тела, ограниченного поверхностями , 
, 
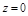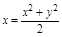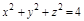
1. Область V в правильная в направлении оси Oz, а область D неправильная во всех направлениях.
2. Перейдем в цилиндрическую систему координат
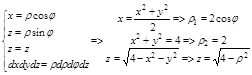
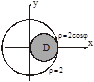
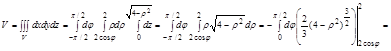
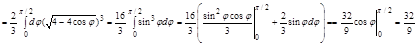
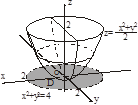Задача. Вычислить тройной интеграл 
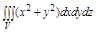, где V: ограничена плоскостью z=2 и параболоидом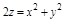 
1. Область V правильная в направлении оси Oz в пределах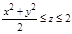 
2. Область D, проекция тела V в плоскости xOy, правильная во всех направлениях и представляет окружность, для удобства вычисления перейдем к цилиндрической системе координат:
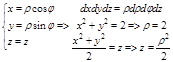Þ D: 
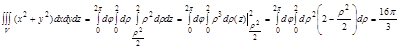
Примечание: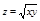 
- конус.
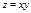- гиперболический параболоид (повернутый)
Приложение тройного интеграла.
Переход к цилиндрическим координатам.
Задача. Вычислить объем тела ограниченного сферой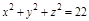 
и поверхностью параболоида 
.
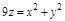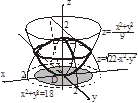1. Тело V правильное в направлении оси Oz в пределах:
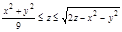
2. Область D проекция тела в область xOy правильно во всех направлениях и представляет окружность
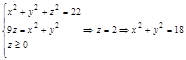
3. Для удобства вычисления перейдем к цилиндрической системе координат:
|
|
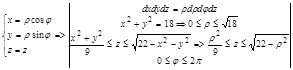
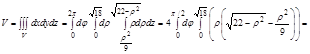
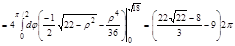
Задача. Найти массу тела заданного ограничивающими его поверхностями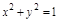 
, 
, 
, 
, 
(
, 
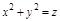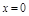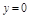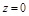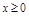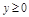) с плотностью 
.
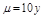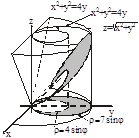Задача. Найти массу тела заданного ограничивающими его поверхностями 
, 
, 
, 
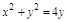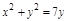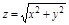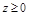с плотностью 
.
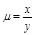1. а.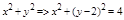 
– цилиндр R=2, центр (0;2)
б.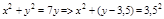 
– цилиндр R =3,5, центр (0;3,5)
в.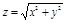 
– конус
2. Для удобства вычисления перейдем в цилиндрическую систему координат
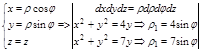
3. V’: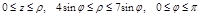 
, 
