Исходя из энергетической теории прочности подберем толщину пластинки h.

ВАРИАНТ 9

Числовые значения:

Функция прогибов:

Уравнение поперечной нагрузки:

Схема пластинки:

A B x

D a C

Рис. 1. Расчётная схема пластинки.

Условие задания:

1. Установить граничные условия, которым удовлетворяет функция прогибов w(x, y).

2. Проверить, удовлетворяет ли функция w(x, y) уравнению Софи Жермен , и если это не так, то использовать уравнение Бубнова-Галеркина: .

Из этих уравнений определить постоянную C и вычислить W_MAX (максимальный прогиб).

3. По формулам для M_X, M_Y, M_XY, Q_X, Q_Y составить их выражения.

4. В опасных сечениях пластинки построить эпюры M_X, M_XY, Q_X в сечении перпендикулярном оси x и эпюры M_Y, M_XY, Q_Y в сечении перпендикулярном оси y.

5. В этих же сечениях пластинки построить эпюры напряжений s_X, s_Y, t_XY, t_ZX, t_ZY по ее толщине.

6. Исходя из энергетической теории прочности подобрать толщину пластинки h.

— погонный изгибающий момент в сечении с нормалью x;

— погонный изгибающий момент в сечении с нормалью y;

— погонные крутящие моменты в тех же сечениях;

— погонная перерезывающая (поперечная) сила в сечении с нормалью x;

— погонная перерезывающая (поперечная) сила в сечении с нормалью y;

Определим граничные условия пластинки.

Возьмем производные функции прогибов w:

Дифференцируем по x:

Дифференцируем по y:

a) При x=0;

При x=a;

b) При y=0;

При y=b;

Из пунктов a и b следует, что пластина не имеет свободного края.

c) При x=0:

Сторона AD — не защемлена.,

d) x=а:

Сторона ВC — не защемлена.

e) y=0:

Сторона AВ — не защемлена.

f) y=b:

Сторона CD — не защемлена.

Проверим шарнирное опирание:

;

при ;

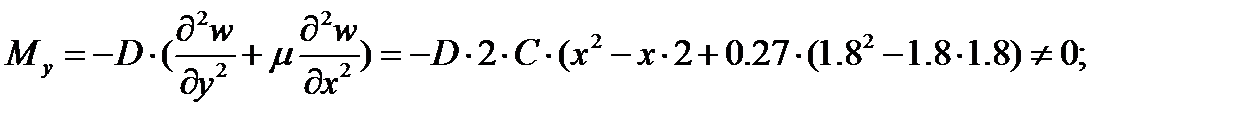
Рис. 2. Схема закрепления пластинки.

2. Проверим, удовлетворяется ли уравнение Софи Жермен. Для этого вычислим производные:

Подставим значения производных и q(x, y) в уравнение :

Равенство не выполняется, т. к. слева стоит постоянная величина 8С, а справа – переменная.

Применим метод Бубнова-Галеркина.

Постоянную C берем из распечатки — С=0,066/D.

Анализируя пластинку определяем координаты максимального прогиба (x=a/2м, y=b/2м) и находим максимальный прогиб:

3. По формулам для M_X, M_Y, M_XY, Q_X, Q_Y составим их выражения.

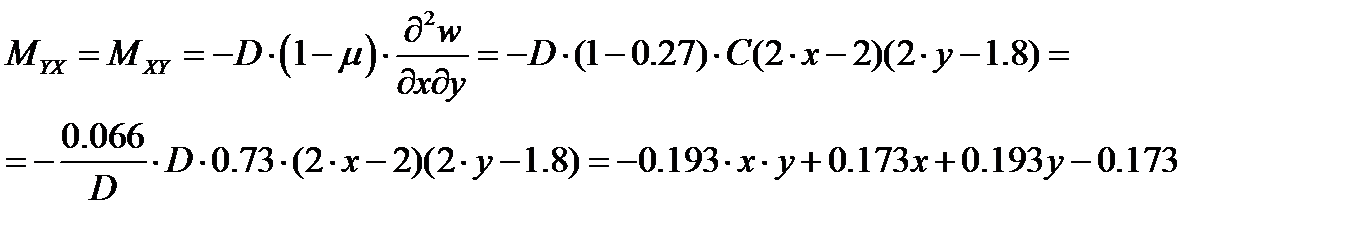
4. В опасных сечениях пластинки построим эпюры M_X, M_XY, Q_X в сечении перпендикулярном оси x и эпюры M_Y, M_XY, Q_Y в сечении перпендикулярном оси y.

5. В опасных сечениях пластинки построим эпюры напряжений s_X, s_Y, так как в этих сечениях M_yx=M_xy=Q_x=Q_y=0, то напряжения t_xy, t_zy, t_zx в них отсутствуют

Построим эпюры в сечении х=0м, у=0м.

§ При z=0

§ При z=h/2

Исходя из энергетической теории прочности подберем толщину пластинки h.

Условие прочности имеет вид:

Главные напряжения определяем как корни кубического уравнения:

где: I₁, I₂, I₃ — инварианты напряженного состояния.

Напряжением s_Z пренебрегают. Кроме того, в нашем случае

Поэтому инварианты имеют вид:

Кубическое уравнение принимает вид: , откуда s₃=0

Окончательно принимаем h = 6см

Найдём численное значение максимального прогиба:

НОМЕР ВАРИАНТА 9

Размеpы пластинки Ax = 2.00 м By = 1.80 м Нагpузка Qo = 2.30 MПa

Значение коэффициента С = .066/D

Значения моментов Mx [10^3 кН*м/м]

.000 .013 .023 .030 .034 .035 .034 .030 .023 .013 .000

.038 .051 .061 .068 .072 .074 .072 .068 .061 .051 .038

.068 .081 .091 .098 .102 .103 .102 .098 .091 .081 .068

.089 .102 .112 .119 .123 .125 .123 .119 .112 .102 .089

.102 .115 .125 .132 .136 .137 .136 .132 .125 .115 .102

.106 .119 .129 .136 .140 .142 .140 .136 .129 .119 .106

.102 .115 .125 .132 .136 .137 .136 .132 .125 .115 .102

.089 .102 .112 .119 .123 .125 .123 .119 .112 .102 .089

.068 .081 .091 .098 .102 .103 .102 .098 .091 .081 .068

.038 .051 .061 .068 .072 .074 .072 .068 .061 .051 .038

.000 .013 .023 .030 .034 .035 .034 .030 .023 .013 .000

Значения моментов My [10^3 кН*м/м]

.000 .047 .084 .110 .126 .131 .126 .110 .084 .047 .000

.010 .058 .094 .120 .136 .141 .136 .120 .094 .058 .010

.018 .066 .102 .128 .144 .149 .144 .128 .102 .066 .018

.024 .071 .108 .134 .150 .155 .150 .134 .108 .071 .024

.028 .075 .111 .138 .153 .159 .153 .138 .111 .075 .028

.029 .076 .113 .139 .154 .160 .154 .139 .113 .076 .029

.028 .075 .111 .138 .153 .159 .153 .138 .111 .075 .028

.024 .071 .108 .134 .150 .155 .150 .134 .108 .071 .024

.018 .066 .102 .128 .144 .149 .144 .128 .102 .066 .018

.010 .058 .094 .120 .136 .141 .136 .120 .094 .058 .010

.000 .047 .084 .110 .126 .131 .126 .110 .084 .047 .000

Значения моментов Mxy=Myx [10^3 кН*м/м]

-.172 -.138 -.103 -.069 -.034 .000 .034 .069 .103 .138 .172

-.138 -.110 -.083 -.055 -.028 .000 .028 .055 .083 .110 .138

-.103 -.083 -.062 -.041 -.021 .000 .021 .041 .062 .083 .103

-.069 -.055 -.041 -.028 -.014 .000 .014 .028 .041 .055 .069

-.034 -.028 -.021 -.014 -.007 .000 .007 .014 .021 .028 .034

.000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000

.034 .028 .021 .014 .007 .000 -.007 -.014 -.021 -.028 -.034

.069 .055 .041 .028 .014 .000 -.014 -.028 -.041 -.055 -.069

.103 .083 .062 .041 .021 .000 -.021 -.041 -.062 -.083 -.103

.138 .110 .083 .055 .028 .000 -.028 -.055 -.083 -.110 -.138

.172 .138 .103 .069 .034 .000 -.034 -.069 -.103 -.138 -.172

Значения попеpечных сил Qx [10^3 кН/м]

.262 .210 .157 .105 .052 .000 -.052 -.105 -.157 -.210 -.262

Значения попеpечных сил Qy [10^3 кН/м]

.236 .236 .236 .236 .236 .236 .236 .236 .236 .236 .236

.189 .189 .189 .189 .189 .189 .189 .189 .189 .189 .189

.142 .142 .142 .142 .142 .142 .142 .142 .142 .142 .142

.094 .094 .094 .094 .094 .094 .094 .094 .094 .094 .094

.047 .047 .047 .047 .047 .047 .047 .047 .047 .047 .047

.000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000

-.047 -.047 -.047 -.047 -.047 -.047 -.047 -.047 -.047 -.047 -.047

-.094 -.094 -.094 -.094 -.094 -.094 -.094 -.094 -.094 -.094 -.094

-.142 -.142 -.142 -.142 -.142 -.142 -.142 -.142 -.142 -.142 -.142

-.189 -.189 -.189 -.189 -.189 -.189 -.189 -.189 -.189 -.189 -.189

-.236 -.236 -.236 -.236 -.236 -.236 -.236 -.236 -.236 -.236 -.236

Исходя из энергетической теории прочности подберем толщину пластинки h.

Поиск по сайту