ТЕОРИЯ ГРАФОВ - это область дискретной математики, особенностью которой является геометрический подход к изучению объектов. Обычно её относят к топологии (потому что во многих случаях рассматриваются лишь топологические свойства графов), однако она пересекается со многими разделами теории множеств, комбинаторной математики, алгебры, геометрии, теории матриц, теории игр, математической логики и многих других математических дисциплин. Основной объект теории графов- граф и его обобщения.
Одним из первых результатов в теории графов явился критерий существования обхода всех ребер графа без повторений, полученный Л. Эйлером при решении задачи о Кенигсбергских мостах. Вот пересказ отрывка из письма Эйлера от 13 марта 1736 году: ” Мне была предложена задача об острове, расположенном в городе Кенигсберге и окруженном рекой, через которую перекинуто 7 мостов. Спрашивается, может ли кто-нибудь непрерывно обойти их, проходя только однажды через каждый мост. И тут же мне было сообщено, что никто еще до сих пор не смог это проделать, но никто и не доказал, что это невозможно. Вопрос этот, хотя и банальный, показался мне, однако, достойным внимания тем, что для его решения недостаточны ни геометрия, ни алгебра, ни комбинаторное искусство. После долгих размышлений я нашел лёгкое правило, основанное на вполне убедительном доказательстве, с помощью которого можно во всех задачах такого рода тотчас же определить, может ли быть совершен такой обход через какое угодно число и как угодно расположенных мостов или не может“. Кенигсбергские мосты схематически можно изобразить так:
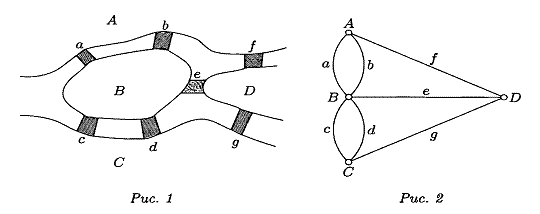
Город Кенигсберг (сейчас Калининград) располагался на обоих берегах реки Прегель и на двух островах, которые соединялись семью мостами. План расположения мостов приведен на рис.1. Задача, о корой говорится в письме, состоит в том, чтобы во время прогулки пройти каждый мост по одному разу и вернуться в исходную точку.
Так как нас интересуют только переходы по мостам, то план города можно заменить схемой (рис.2). На схеме земельные участки, разделенные рукавами реки, как бы сжаты в точки A,B,C,D (вершины), а мосты вытянуты в линии a,b,c,d,e,f,g (ребра). Нетрудно проверить (например, перебрав все возможные варианты), что изображенную фигуру нельзя обвести карандашом, не отрывая его от бумаги и проходя по каждой дуге ровно один раз.
Исследуя ситуацию с кенигсбергскими мостами, Эйлер решил значительно более общую задачу. Для того чтобы лучше понять полученный им результат, введем некоторые определения.

Фигура, состоящая из точек (вершин) и соединяющих их линий (ребер), называется графом (рис. 3). Маршрутом, или путем, соединяющим вершины A и B графа, называется такая последовательность его ребер, в которой каждые два ребра имеют общую концевую точку, причем первое ребро выходит из вершины A, а последнее входит в вершину B (рис. 4). В этом случае вершины A и B называются связанными. Граф называется связным, если любая пара его вершин связана (рис. 5). Граф на рис. 6 несвязен.

Маршрут называется цепью, если каждое ребро графа встречается в нем не более одного раза (вершины в цепи могут повторятся и несколько раз) (рис.7). Цепь, начальная и конечная вершины которой совпадают, называется циклом (рис. 8).

Вершина называется четной, если в ней сходится четное число ребер, и нечетной, если число сходящихся в ней ребер нечетно. Вершина Aна рис. 9 четна – в ней сходится 6 ребер, а вершина B нечетна – в ней сходится 5 ребер. Число ребер, сходящихся в вершине графа, называют степенью (порядком) этой вершины.

Наконец, граф называется конечным, если множество его ребер конечно. Примером бесконечного графа может служить прямоугольная сетка, заданная на всей плоскости.
Теорема (Эйлер). В любом конечном связном графе, все вершины которого четны, существует цикл, в котором каждое ребро графа участвует ровно один раз.
Такой граф называется эйлеровым циклом, а граф, все вершины которого четны (и, значит, существует эйлеров цикл), - эйлерововым графом.
Обратившись к графу в задаче о кенигсбергских мостах, замечаем, что все четыре его вершины являются нечетными – в вершинах A,C,D сходятся по три ребра, а в вершине B – пять ребер. Значит, этот граф не эйлеров.
Важный класс графов составляют так называемые деревья. Деревом называется связный граф, который не имеет циклов (рис. 10).
Число В вершин дерева и число Р его ребер различаются на единицу: В=Р+1.

Рис. 10.
Сети
В приложениях граф обычно интерпретируется как сеть, а его вершины называют узлами.
Дерево решений
Для принятия важных решений для выбора наилучшего направления действий из имеющихся вариантов используется так называемое дерево решений, представляющее собой схематическое описание проблемы принятия решений.
Применение дерева решений подразумевает понимание (хотя бы интуитивное) таких понятий, как «вероятность» и «ожидаемое значение (математическое ожидание) случайной величины». Подробно эти вопросы будут изучены далее.
Пример. По настоянию родителей выпускник американской школы должен продолжить учебу. Свободный в своем выборе, он хочет оценить возможности получения диплома в области инжиниринга или в области бизнеса в одном из двух университетов – в университете родного города Йорка и в университете штата, понимая, что вероятность успеха зависит от выбора как университета, так и будущей специальности.
1. Если он останавливает свой выбор на университете штата и бизнесе, то вероятность успеха (получение диплома) считается равной 0,6.
2. Если он останавливает свой выбор на университете штата и инжиниринге, то вероятность успеха считается равной 0,7.
3. Если он останавливает свой выбор на университете города и бизнесе, то вероятность успеха считается равной 0,9.
4. Если он останавливает свой выбор на университете города и инжиниринге, то вероятность успеха считается равной 0,95.
5. Средний доход за год в течение первых 5 лет выпускника бизнес-школы университета штата при условии полной занятости составляет 35 тыс.долл.
6. Средний доход за год в течение первых 5 лет у окончившего школу инжиниринга университета штата при условии полной занятости составляет 30 тыс.долл.
7. Средний доход за год в течение первых 5 лет выпускника бизнес-школы университета города при условии полной занятости составляет 24 тыс.долл.
8. Средний доход за год в течение первых 5 лет у окончившего школу инжиниринга университета города при условии полной занятости составляет 25 тыс.долл.
9. Если по каким-либо причинам выпускник не поступает ни в один из этих университетов, то его средний доход в течение тех же 5 лет при условии полной занятости будет равен 18 тыс.долл.
Предположим, что единственным критерием при принятии окончательного решения является величина ожидаемого среднего дохода в первые 5 лет трудовой деятельности. Сделав это предположение, попробуем решить проблему выпускника, используя дерево решений.

Рис. 11.
Поясним обозначения на рисунке:
S1 – окончание бизнес-школы университета штата,
S2 – либо неудача при поступлении в бизнес-школу университета штата, либо невозможность завершения обучения,
S3 – окончание школы инжиниринга университета штата,
S4 – либо неудача при поступлении в школу инжиниринга университета штата, либо невозможность завершения обучения,
S5 – окончание бизнес-школы университета города,
S6 – либо неудача при поступлении в бизнес-школу университета города, либо невозможность завершения обучения,
S7 – окончание школы инжиниринга университета города,
S8 – либо неудача при поступлении в школу инжиниринга университета города, либо невозможность завершения обучения,
d1 – выбор университета штата,
d2 – выбор университета города,
d3 – предпочтение отдано бизнесу,
d4 – предпочтение отдано инжинирингу.
Узлы дерева, в которых делается выбор, обозначены квадратиками; узлы дерева, которые принимающий решение не контролирует, – кружками.
Эти два типа узлов рассчитываются по-разному.
При расчете узлов 4-7 определяются ожидаемые значения:
значение в узле 7 N7=0,95*25000+0,05*18000=24650 долл.,
значение в узле 6 N6=0,9*24000+0,1*18000=23400 долл.,
значение в узле 5 N5=0,7*30000+0,3*18000=26400 долл.,
значение в узле 4 N4=0,6*35000+0,4*18000=28200 долл.
Значение N3 в узле 3 определяется так:
Вследствие того что N7 > N6,полагаем N3 = N7 и считаем, что выбор d4 предпочтительнее выбора d3. Тогда N3=24650 долл.
Значение N2 в узле 2 определяется так:
Вследствие того что N4 > N5,полагаем N2 = N4 и считаем, что выбор d3 предпочтительнее выбора d4. Тогда N2=28200 долл.
Значение N1 в узле 1 определяется так:
Вследствие того что N2 > N3,полагаем N1 = N2 и считаем, что выбор d1 предпочтительнее выбора d2. Тогда N1=28200 долл.
Наносим результаты расчетов на рис. 11 и принимаем окончательное решение (рис. 12).

Рис. 12.