Лекция 7. Взаимосвязь силовых и
Энергетических характеристик
Магнитного поля
План лекции
7.1. Циркуляция вектора магнитной индукции для магнитного поля в вакууме.
7.2. Действие магнитного поля на проводники с током и движущиеся заряды.
7.3. Поток вектора магнитной индукции. Теорема Гаусса для магнитного поля.
Работа по перемещению проводника с током и контура с током в магнитном поле.
Циркуляция вектора магнитной индукции для магнитного поля в вакууме
Аналогично циркуляции вектора напряженности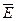 
электрического поля вводится понятие - циркуляция вектора магнитной индукции. Циркуляцией вектора 
по заданному замкнутому контуру называется интеграл
, (7.1)
где 
- вектор элемента длины контура; 
- угол между векторами и ; 
- проекция на направление .
В теоретической электродинамике доказывается теорема о циркуляции вектора (закон полного тока для магнитного поля в вакууме): циркуляция вектора по произвольному замкнутому контуру равна произведению магнитной постоянной на алгебраическую сумму токов, охватываемых этим контуром
. (7.2)
Здесь n - число проводников с токами, охватываемых контуром L. В дифференциальной форме для данной точки поля 
, где 
- плотность тока в этой точке. Поэтому магнитное поле является вихревым в отличие от потенциального электростатического поля. Каждый ток учитывается столько раз, сколько он охватывается контуром. Положительным считается ток, направление которого связано с произвольно выбранным направлением обхода по контуру правилом правого винта. Ток противоположного направления считается отрицательным. Закон полного тока позволяет рассчитывать магнитные поля разной конфигурации, гораздо проще, чем с помощью закона Био-Савара-Лапласа в сочетании с принципом суперпозиции магнитных полей.
Проиллюстрируем это выводом формулы магнитного поля прямого тока (тока, текущего по тонкому прямому проводу бесконечной длины), перпендикулярного плоскости чертежа и направленного к нам (рис. 7.1). Возьмем в качестве произвольного замкнутого контура L окружность радиуса R. В каждой точке этого контура вектор одинаков по модулю и направлен по касательной к контуру L (окружность, которая одновременно и является линией магнитной индукции, то есть 
). Циркуляция вектора (по закону полного тока) равна (7.2) 
, откуда окончательно получаем
. (7.3)
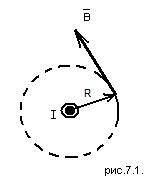
Рис. 7.1
Сравнивая выражение (2.3) и (7.2) для циркуляции векторов 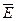и можно увидеть принципиальную разницу. Циркуляция вектора 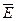электростатического поля всегда равна нулю, то есть электростатическое поле является потенциальным. Циркуляция же вектора магнитного поля не равна нулю. Такое поле называется вихревым. Таким образом теорема о циркуляции вектора имеет в учении о магнетизме такое же значение, как теорема Гаусса в электростатике, так как позволяет находить магнитную индукцию поля без использования закона Био-Савара-Лапласа.
Действие магнитного поля на проводники с током и движущиеся заряды
Из ориентирующего действия магнитного поля на рамку с током следует, что на стороны рамки (проводники с током) действует сила со стороны магнитного поля. Ампером было установлено, что эти силы определяются следующим соотношением (законом Ампера):
(7.4)
или соответственно
(7.5)
где 
- сила, действующая со стороны магнитного поля на элемент проводника 
, по которому течет ток J; - угол между векторами 
и 
.
Из (7.4) следует, что вектор 
направлен как векторное произведение векторов и , откуда и формируется вспомогательное правило левой руки: если ладонь левой руки расположить так, что бы в неё входил вектор , а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы Ампера. Закон Ампера позволяет выяснить физический смысл модуля вектора магнитной индукции: «основной силовой характеристики магнитного поля». Из (7.5) следует, что
. (7.6)
При J = 1 А, l = l м, sin α = 1 из (7.6) вытекает, что B = F A, то есть модуль вектора магнитной индукции равен силе Ампера, действующей на проводник с током единичной длины, по которому течет единичный ток и который перпендикулярен направлению поля. В «СИ» единица магнитной индукции - 1 Тесла [Тл = Н/(А·м)].
Из закона Ампера следует, что воздействие одного тока на другой должно носить характер взаимодействия (рис. 7.2). Каждый из двух бесконечных прямолинейных токов J 1 и J 2 (расстояние между которыми R) создают магнитное поле, которое действует на другой проводник с током.
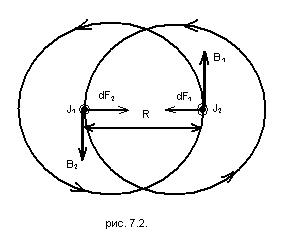
Рис. 7.2
Ток J 1 создает магнитное поле, направление которого 
задается правилом правого винта (см. рис. 7.2), а его модуль, согласно (7.3) равен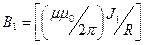 
. Направление силы 
, с которой поле действует на участок второго тока, определяется по правилу левой руки (см. рис. 7.2). Модуль в соответствии с (7.3) равен 
и далее
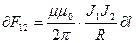. (7.7)
Рассуждая аналогично можно показать, что сила 
, с которой магнитное поле 
действует на элемент первого проводника с током 
направлена в противоположную сторону и равна по модулю
, (7.8)
то есть два параллельных тока одинакового направления притягиваются друг к другу силой
. (7.9)
Соответственно между токами противоположного направления действует сила отталкивания, определяемая выражением (7.9).
Так как магнитное поле действует на проводники с током, в которых движутся заряды, то оно должно действовать и на один электрический заряд Q, движущийся в магнитном поле со скоростью 
. Такая сила получила название сила Лоренца и выражается формулой 
или
, (7.10)
где - угол между векторами и . Направление силы Лоренца определяется с помощью модифицированного правила левой руки: если ладонь левой руки расположить так, что бы в нее входил вектор , а четыре вытянутых пальца направить вдоль вектора для Q > 0 (и против вектора для Q < 0), то отогнутый большой палец покажет направление силы Лоренца.
Согласно (7.10) 
, то есть сила Лоренца работы не совершает, и кинетическая энергия заряженной частицы не меняется. Таким образом, при движении заряженной частицы в магнитном поле её скорость не меняется по величине, а меняется только по направлению. Соотношение (7.10) позволяет проанализировать возможные варианты движения заряженных частиц в однородном магнитном поле. Рассмотрим простейшие частные случаи и общий случай этого движения.
Если заряженная частица движется со скоростью вдоль линий магнитной индукции (угол между векторами и равен нулю или 
), то по формуле (7.10) сила Лоренца равна нулю. И согласно первому закону Ньютона частица движется прямолинейно и равномерно. Если заряженная частица влетает в магнитное поле со скоростью , перпендикулярной вектору , то сила Лоренца (7.10) 
- постоянна по модулю, то есть согласно второму закону Ньютона эта сила создает центростремительное ускорение: 
, откуда
(7.11)
- радиус окружности, по которой равномерно вращается частица в плоскости, перпендикулярной полю в этом случае.
Если скорость заряженной частицы (например, электрона Q < 0) направлена под углом к вектору (рис. 7.3), то её движение можно представить в виде суперпозиции двух движений: 1) равномерного прямолинейного движения вдоль поля со скоростью 
; 2) равномерного вращения со скоростью 
по окружности в плоскости, перпендикулярной полю. Радиус окружности согласно (7.11) равен
. (7.12)
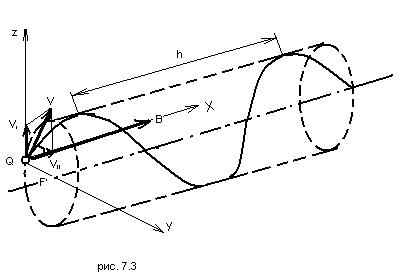
Рис. 7.3
В результате сложения обоих движений частица начинает двигаться по спирали (ось которой параллельна ). Период вращения частицы по спирали (время одного оборота) 
и с учётом (7.12) получим 
. Шаг винтовой линии (путь, проходимый частицей вдоль поля за один оборот)
. (7.13)
Если скорость заряженной частицы составляет угол с направлением неоднородного магнитного поля, индукция которого возрастает в направлении движения частицы, то и r и h спирали уменьшаются с ростом В. На этом эффекте основана фокусировка заряженных частиц в магнитном поле.