ОБРАБОТКА РЕЗУЛЬТАТОВ ТАХЕОМЕТРИЧЕСКОЙ
СЪЕМКИ И ПОСТРОЕНИЕ ПЛАНА УЧАСТКА МЕСТНОСТИ
Вариант Р6
Исходные данные:
αА-I = 59º12.5';
αIV-В = 209º42.5';
хI = 5217.90м;
yI = 3324.43м;
xIV = 4918.13м;
yIV = 3330.60м;
H1 = 44.37м.
Рис. 1 Схема теодолитно-высотного хода
Ход решения:
Вычисляем суммуизмеренных углов хода в соответствии со схемой (рис. 1), получаем 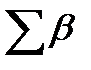 изм = 569°30.7’.
изм = 569°30.7’.
Вычисляем теоретическую сумму углов по формуле:
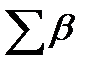 т =
т = 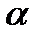 нач -
нач - 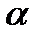 кон +1800· n,
кон +1800· n,
где n – число точек хода.
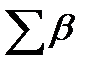 т =59º12.5'–209º42.5' + 180° · 4 = 569°30′.
т =59º12.5'–209º42.5' + 180° · 4 = 569°30′.
Вычисляем угловую невязку f 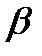 по формуле
по формуле
f 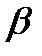 =
=  изм -
изм - 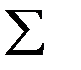
 т.
т.
f 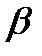 = 569°30.7’ – 569°30′ = +0°00.7’
= 569°30.7’ – 569°30′ = +0°00.7’
Вычислить допустимую угловую невязку по формуле
f 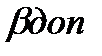 = 1’·
= 1’· 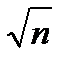 ;
;
f 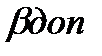 = 1′
= 1′  = 2′.
= 2′.
Так как фактическая невязка получилась меньше допустимой (0.7’ < 2’), то полученную невязку распределяем с обратным знаком поровну на все углы хода с округлением до десятых долей минуты: νβ 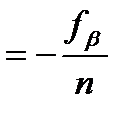 . В нашем случае поправка в три угла составляет 0.2’, и в один угол 0.1′. Контроль введения поправок выполняется
. В нашем случае поправка в три угла составляет 0.2’, и в один угол 0.1′. Контроль введения поправок выполняется 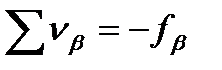 .
.
Вычислить уравненные значения углов βур по формуле:
βур = βизм + νβ.
Результаты вычислений занесены в колонку исправленных углов.
В результате введения поправок сумма уравненных углов стала равна теоретической сумме (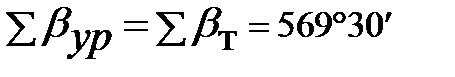 ).
).
Вычисление дирекционных углов сторон хода и приращений координат
Вычисляем дирекционные углы линий в соответствии с формулой:
αn = αn-1 + 180° - βn.
Например, вычислим дирекционный угол стороны I-II
αI-II = 59º12.5' + 180° − 99°59.9′ = 139°12.6′
Результаты вычислений сведены в колонку дирекционных угловтаблицы 2. Вычисленное значение конечного дирекционного угла αIV-Bравняется исходному значению, следовательно, дирекционные углы вычислены верно.
Вычисление горизонтальных проложений сторон хода и приращений координат.
Горизонтальные проложения линий находим по формуле:
d=D · cos ν.
Приведем пример:
dI-II = 120.65·cos2º50' = 120.50м;
dII-III = 136.18·cos2º55' + 50.41·cos6º20' = 186.10мит.д.
Результаты вычислений сведены в таблицы 1 и 2.
Таблица 1
Вычисление горизонтальных проложений
| Линия | Длина линии | Угол наклона | Горизонтальное проложение |
| I-II | 120.65 | 2°50¢ | 120.50 |
| II - III | 136.18 50.41 | 2°55¢ 6°20¢ | 136.00 + 50.10 186.10 |
| III - IV | 104.12 46.43 | 2°45¢ 5°40¢ | 104.00 + 46.20 150.20 |
Вычисляем приращения координат между пунктами хода по формулам:
Δ x = S · cosα;
Δ y = S · sinα.
Например, приращения координат между пунктами I и II будут равны:
Δx = 120.50 · cos139º12.6' = -91.23м;
Δy = 120.50 · sin139º12.6' = +78.72м.
Результаты вычислений приращений координат сведены в одноименные колонки таблицы 2.
Вычисление абсолютной и относительной линейных невязок хода. Уравнение приращений координат
Вычисляем невязки ƒ x и ƒ y в приращениях координат по осям х и у по формулам:
ƒx = ΣΔ xвыч − ΣΔ xт;
ƒу = ΣΔ увыч − ΣΔ ут.
где
ΣΔ xт = хкон − хнач;
ΣΔ ут = укон − унач.
Для нашего хода получаем:
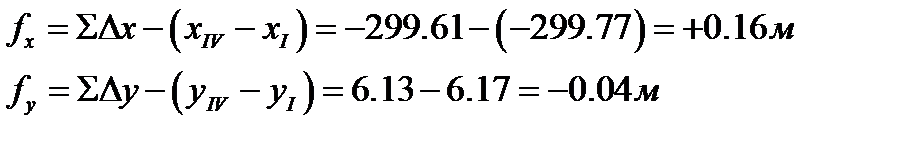
Вычисляем абсолютную линейную невязку ƒр хода по формуле:
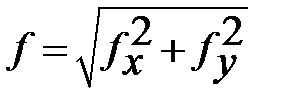 .
.

Вычисляем относительную линейную невязку хода поформуле:
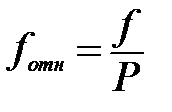
где Р - сумма длин сторон хода.
Подставив числовые значения, получаем:
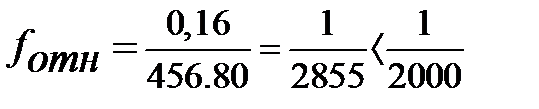 .
.
Распределяем невязки ƒх и ƒу, вводя поправки νx и νy в вычисленные значения приращений координат пропорционально длинам сторон в соответствии с формулами:
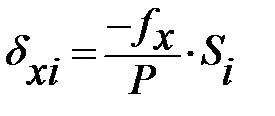 ;
; 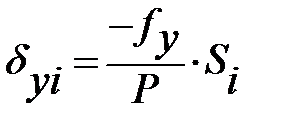 ,
,
где Si – длина стороны хода, для которой вычисляется поправка в приращении Δxi Δyi.
В качестве примера приведем вычисление поправок в приращения координат стороны хода I-II:
 ;
; 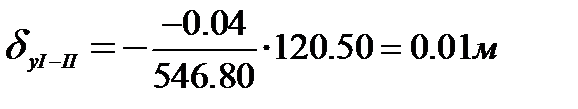 .
.
Вычисленные поправки в приращения координат сведены в Таблицу 2и надписаны над соответствующими вычисленными приращениями.
Контроль выполнен: суммы поправок равны соответствующим линейным невязкам с противоположным знаком (−ƒx = Σ δxi = -0.16 м и −ƒу = Σ δуi = +0.04м).
Вычисляем уравненные значения Δxур и Δуур по формулам:
Δ xур = Δ xвыч + δх;
Δ уур = Δ увыч + δу;
Так уравненные приращения координат стороны хода I-II будут равны:
Δ xурI-II = -91.23м– 0,04м = -91.27м;
Δ уурI-II = 78.72м+ 0,01м = +78.73м.
Аналогично вычисляются уравненные приращения остальных сторон хода. Уравненные приращения координат записываем в Таблицу 2 в соответствующую колонку.
В результате введения поправок сумма уравненных приращений координат стала равна теоретической сумме приращений (ΣΔ xур = ΣΔ xт = -299.776м и ΣΔ уур = ΣΔ ут = 6.17м), что подтверждает верность выполненных вычислений.
Вычисление координат точек хода
Вычисляемкоординаты точек хода путем последовательного алгебраического сложения координат предыдущих точек с соответствующими уравненными приращениями по формулам:
xn = xn-1 + Δxn;
yn = yn-1 + yxn.
Так координаты точки II будут вычисляться следующим образом:
хII = xI + ΔxI-II = 5217.90–91.27 = 5126.63 м;
уII = уI + ΔуI-II = 3324.43+78.73 = 3403.16 м и т.д.
Результаты вычислений координат сведены в Таблицу 2. Полученные в конце вычислений координаты IV равны исходным данным, следовательно, уравнивание теодолитного хода и вычисление координат станций выполнено верно.
Таблица 2
Ведомость вычисления координат разомкнутого теодолитного хода
| №№ точек | Углы измеренные | Углы исправленные | Дирекционные углы | Горизонтальные проложения d, м | Приращения координат (вычисленные) | Приращения координат (уравненные) | Координаты | №№ точек | ||||||
| ° | ' | ° | ' | ° | ' | ΔХ | ΔУ | ΔХ | ΔУ | Х | У | |||
| А | А | |||||||||||||
| -0.2 | 12.5 | |||||||||||||
| I | 0.1 | 59.9 | -0.04 | +0.01 | 5217.90 | 3324.43 | I | |||||||
| -0.2 | 12.6 | 120.50 | -91.23 | 78.72 | -91.27 | 78.73 | ||||||||
| II | 17.3 | 17.1 | -0.07 | +0.02 | 5126.63 | 3403.16 | II | |||||||
| -0.2 | 55.5 | 186.10 | -171.21 | 72.94 | -171.28 | 72.96 | ||||||||
| III | 15.3 | 15.1 | -0.05 | +0.01 | 4955.35 | 3476.12 | III | |||||||
| -0.1 | 40.4 | 150.20 | -37.17 | -145.53 | -37.22 | -145.52 | ||||||||
| IV | 57.9 | 4918.13 | 3330.60 | IV | ||||||||||
| 42.5 | ΣΔx= -299.61 | ΣΔу= 6.13 | ||||||||||||
| B | Р=Σd=456.80 | B |
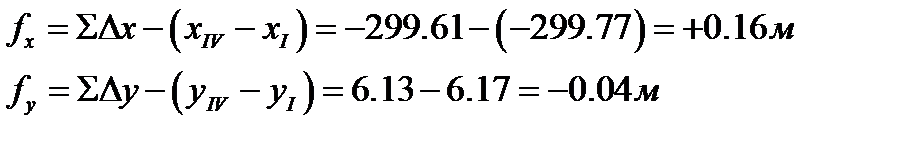 fабс=
fабс= 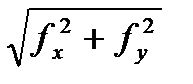 = = 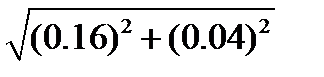 =0.16
fотн= =0.16
fотн= 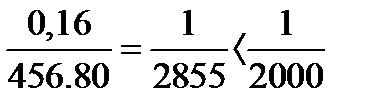
|
Σβтеор= αнач – αкон +180°· n =569°30'
fβ= Σβизм – Σβтеор=0.7'
fβдоп = ±1’ 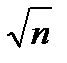 =±2.0'
=±2.0'
Вычисление высот точек хода и съемочных пикетов
Вычисляем отметки точек хода по формуле:
Нi+1 = Hi + h
Приведем пример
Н2 = 44.37 + 4.80 = 49.17м и т.д.
Вычисленные отметки точек хода сведены в Таблицу 3.
Таблица 3
Вычисление отметок точек теодолитно-высотного хода
| № точки | Превышение h, м | Отметки точек Н, м |
| I | 44.37 | |
| +4.80 | ||
| II | 49.17 | |
| -1.20 | ||
| III | 47.97 | |
| -0.30 | ||
| IV | 47.67 |
Вычисляем отметки съемочных пикетов в журнале тахеометрической съемки по формуле:
Нi = Нст + hi,
где Нст –отметка съемочной точки, с которой определена отметка съемочного пикета;
hi – превышение между отметкой съемочного пикета и отметкой съемочной точки.
Результаты вычислений сведены в Таблицу 4.
Таблица 4