Усилия трещинообразования для элементов без предварительного напряжения
Изгибающий момент Мcrc при образовании нормальных трещин производят с учетом неупругих деформаций растянутого бетона согласно следующим положениям: а) сечения после деформирования остаются плоскими; б) эпюру напряжений в сжатой зоне бетона принимают треугольной формы, как для упругого тела; в) эпюру напряжений в растянутой зоне бетона принимают трапециевидной формы с напряжениями, не превышающими расчетных значений сопротивления бетона растяжению Rbt,ser; г) относительную деформацию крайнего растянутого волокна бетона принимают равной ее предельному значению 
при кратковременном действии нагрузки, а при двухзначной эпюре деформаций в сечении элемента 
; д) напряжения в арматуре принимают в зависимости от относительных деформаций как для упругого тела.
Допускается момент образования трещин определять без учета неупругих деформаций растянутого бетона. Момент образования трещин без учета неупругих деформаций растянутого бетона определяют как для сплошного упругого тела по формуле
, (7.1)
где W - момент сопротивления сечения для крайнего растянутого волокна бетона, определяемый по формуле 
ея - расстояние от точки приложения продольной силы N (расположенной в центре тяжести приведенного сечения элемента) до ядровой точки, наиболее удаленной от растянутой зоны, трещинообразование которой проверяется, 
; I red - момент инерции приведенного поперечного сечения относительно его центра тяжести, 
A red - площадь сечения приведенного поперечного сечения элемента,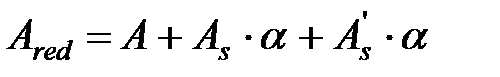 
; a - коэффициент приведения арматуры к бетону, 
; 
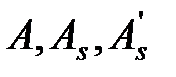- площади поперечного сечения соответственно бетона, растянутой и сжатой арматуры; y t - расстояние от наиболее растянутого волокна бетона до центра тяжести приведенного поперечного сечения элемента, 
; S t,red - статический момент площади приведенного поперечного сечения элемента относительно наиболее растянутого волокна бетона.
|
|
В формуле (7.1) знак “плюс” принимают при сжимающей продольной силе N, “минус” - при растягивающей силе.
Усилие N crc при образовании трещин в центрально растянутых элементах определяют по формуле
(7.2)
Усилия трещинообразования для предварительно напряженных элементов
Момент образования трещин предварительно напряженных изгибаемых элементов без учета неупругих деформаций растянутого бетона определяют как для сплошного упругого тела по формуле
Mcrc Rbt,ser W+P eяр, (7.3)
где eяр = е0р + r - расстояние от точки приложения усилия предварительного обжатия Р до ядровой точки, наиболее удаленной от растянутой зоны, трещинообразование которой проверяется; е0р - то же, до центра тяжести приведенного сечения; r - расстояние от центра тяжести приведенного сечения до ядровой точки.
Усилие Ncrc при образовании трещин в центрально растянутых элементах определяют по формуле
Ncrc = Ared Rbt,ser + Р. (7.4)
7.1.3. Расчет по раскрытию нормальных трещин
Ширину раскрытия нормальных трещин определяют по формуле
, (7.5)
где σs - напряжение в продольной растянутой арматуре в нормальном сечении с трещиной от соответствующей внешней нагрузки, определяемое согласно формуле
; (7.6)
где l s - базовое (без учета влияния вида поверхности арматуры) расстояние между смежными нормальными трещинами, 
, принимаемое не менее 10 ds и 10 см и не более 40 ds и 40 см (для элементов с рабочей высотой поперечного сечения не более 1 м); Аbt - площадь сечения растянутого бетона (в любом случае значение Аbt принимают равным площади сечения при ее высоте в пределах не менее 2а и не более 0,5 h); As - площадь сечения растянутой арматуры; ds - номинальный диаметр арматуры; ψs - коэффициент, учитывающий неравномерное распределение относительных деформаций растянутой арматуры между трещинами, 
; σs,crc - напряжение в продольной растянутой арматуре в сечении с трещиной сразу после образования нормальных трещин, определяемое при М=Мсrс; σs - то же, при действии рассматриваемой нагрузки; φ1 - коэффициент, учитывающий продолжительность действия нагрузки, принимаемый равным: 1,0 - при непродолжительном действии нагрузки; 1,4 - при продолжительном действии нагрузки; φ2 - коэффициент, учитывающий профиль продольной арматуры, принимаемый равным: 0,5 - для арматуры периодического профиля и канатной; 0,8 - для гладкой арматуры (класса А240); φ3 - коэффициент, учитывающий характер нагружения, принимаемый равным: 1,0 - для элементов изгибаемых и внецентренно сжатых; 1,2 - для растянутых элементов. Здесь yc - расстояние от наиболее сжатого волокна до центра тяжести приведенного сечения, определяемые с учетом площади сечения только сжатой зоны бетона, площадей сечения растянутой и сжатой арматуры, принимая в соответствующих формулах значения коэффициента приведения арматуры к бетону αs2=αs1; Np=Р - усилие предварительного обжатия; Мp - изгибающий момент от внешней нагрузки и усилия предварительного обжатия, определяемый по формуле
|
|
Mp=M±Npe0p, (7.7)
|
|
где е0p - расстояние от точки приложения усилия предварительного обжатия Np до центра тяжести приведенного сечения. Знак «- » в формуле (7.7) принимают, когда направления вращений моментов М и Npе0p не совпадают, и «+ » - когда совпадают.
Значение коэффициента приведения арматуры к бетону αsl определяют по формуле
, (7.8)
где Eb,red - приведенный модуль деформации сжатого бетона, учитывающий неупругие деформации сжатого бетона и определяемый по формуле
. (7.9)
Относительную деформацию бетона εb1,red принимают равной 0,0015. Допускается напряжение σs определять по формуле
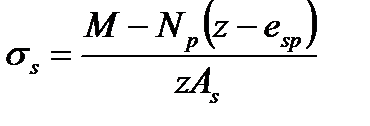, (7.10)
где z - расстояние от центра тяжести арматуры, расположенной в растянутой зоне сечения, до точки приложения равнодействующей усилий в сжатой зоне элемента; еsp - расстояние от центра тяжести той же арматуры до точки приложения усилия Np; напряжения σs не должны превышать (Rs,ser - σsp).
Для элементов прямоугольного поперечного сечения при отсутствии (или без учета) сжатой арматуры значение z определяют по формуле
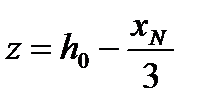, (7.11)
где xN - высота сжатой зоны, определяемая с учетом влияния усилия предварительного обжатия Np;для элементов прямоугольного, таврового (с полкой в сжатой зоне) и двутаврового поперечного сечения допускается значение z принимать равным 0,7 h0.
Для изгибаемых предварительно напряженных элементов положение нейтральной оси определяют из уравнения
, (7.12)
где yN - расстояние от нейтральной оси до точки приложения усилия предварительного обжатия Np; точку приложения усилия Np определяют как для внецентренного сжатия с учетом изгибающего момента М от внешней нагрузки (см. рис. 6.5); Ib0, Is0, I's0, Sb0, Ss0, S's0 - моменты инерции и статические моменты соответственно сжатой зоны бетона, растянутой и сжатой арматуры относительно нейтральной оси.
Допускается для элементов прямоугольного сечения высоту сжатой зоны определять по формуле
, (7.13)
где хM - высота сжатой зоны изгибаемого элемента без учета предварительного напряжения арматуры, определяемая согласно СП 52-101; Ired, Ared - момент инерции и площадь приведенного поперечного сечения, определяемые для полного сечения (без учета трещин); Mp - момент относительно центра тяжести полного приведенного сечения элемента от внешней нагрузки M и усилия предварительного обжатия Npе0p,
Mp=M-Npe0p; e0p - эксцентриситет усилия обжатия Np относительно центра тяжести полного приведенного сечения элемента (без учета момента М). Значения геометрических характеристик сечения элемента определяют по общим правилам расчета сечения упругих элементов.
Рис. 7.1. Приведенное поперечное сечение (а)и схема напряженно-деформированного состояния изгибаемого предварительно напряженного элемента с трещинами (б)при расчете его по деформациям; 1 - уровень центра тяжести приведенного без учета растянутой зоны бетона поперечного сечения
7.1.4. Расчет по деформациям
В общем случае для железобетонных изгибаемых предварительно напряженных элементов вычисление прогиба производят путем разбиения элемента на ряд участков, определения кривизны на границах этих участков (с учетом отсутствия или наличия трещин и знака кривизны) и перемножения эпюр моментов 
и кривизны 
по длине элемента при линейном распределении кривизны в пределах каждого участка. В этом случае прогиб в середине пролета элемента определяют по формуле
, (7.14)
где 
–кривизна элемента соответственно на левой и правой опорах; 
– кривизна элемента в симметрично расположенных сечениях i и i ' (i = i ') соответственно слева и справа от оси симметрии (середины пролета); 
– кривизна элемента в середине пролета; п –четное число равных участков, на которые разделяют пролет, принимаемое не менее 6; l – пролет элемента.
В формуле (7.14) кривизну 
определяют для участков без трещин или с трещинами. Знак величины 
принимают в соответствии с эпюрой кривизны. Для изгибаемых предварительно напряженных элементов постоянного по длине элемента сечения, не имеющих трещин, прогибы определяют по общим правилам строительной механики с использованием жесткости поперечных сечений. Для изгибаемых предварительно напряженных элементов постоянного по длине элемента сечения, имеющих трещины, на каждом участке, в пределах которого изгибающий момент не меняет знак, кривизну допускается вычислять для наиболее напряженного сечения, принимая ее для остальных сечений такого участка изменяющейся пропорционально значениям изгибающего момента. Для свободно опертых или консольных элементов максимальный прогиб определяют по формуле (6.10).
Полную кривизну изгибаемых предварительно напряженных элементов определяют по формулам:
- для участков без трещин в растянутой зоне
; (7.15)
- для участков с трещинами в растянутой зоне
. (7.16)
В формуле (7.15):
- кривизна соответственно от непродолжительного действия кратковременных нагрузок и от продолжительного действия постоянных и временных длительных нагрузок.
В формуле (7.16):
- кривизна от непродолжительного действия всей нагрузки, на которую производят расчет по деформациям; 
- кривизна от непродолжительного действия постоянных и временных длительных нагрузок; 
- кривизна от продолжительного действия постоянных и временных длительных нагрузок.
Кривизну и 
определяют с учетом усилия предварительного обжатия в качестве длительной нагрузки.
Допускается при определении кривизны учитывать влияние деформаций усадки и ползучести бетона в стадии предварительного обжатия. Кривизну изгибаемых предварительно напряженных элементов 
от действия соответствующих нагрузок определяют по формуле
, (7.17)
где М - изгибающий момент от внешней нагрузки; Np и е0p - усилие предварительного обжатия и его эксцентриситет относительно центра тяжести приведенного поперечного сечения элемента; D - изгибная жесткость приведенного поперечного сечения элемента, определяемая по формуле D=Eb1Ired; Еb1 - модуль деформации сжатого бетона, определяемый в зависимости от продолжительности действия нагрузки; Ired - момент инерции приведенного поперечного сечения относительно его центра тяжести, определяемый с учетом наличия или отсутствия трещин.
Значения модуля деформации бетона Еb1 и момента инерции приведенного сечения Ired для элементов без трещин в растянутой зоне и с трещинами определяют соответственно с указаниями определения разных видов жесткости.
7.1.5. Жесткость изгибаемого элемента на участке без трещин в растянутой зоне
Жесткость изгибаемого предварительно напряженного элемента D на участке без трещин. Момент инерции Ired приведенного поперечного сечения элемента относительно его центра тяжести определяют как для сплошного тела по общим правилам сопротивления упругих элементов с учетом всей площади сечения бетона и площадей сечения арматуры с коэффициентом приведения арматуры к бетону α.
Ired = I + Is α +I's α, (7.18)
где I - момент инерции бетонного сечения относительно центра тяжести приведенного поперечного сечения элемента; Is, Is' - момент инерции площади сечения соответственно растянутой и сжатой арматуры относительно центра тяжести приведенного поперечного сечения элемента; 
; 
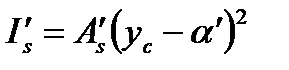; α - коэффициент приведения арматуры к бетону, 
; ус - расстояние от наиболее сжатого волокна бетона до центра тяжести приведенного поперечного сечения элемента.
Значения I и ус определяют по общим правилам расчета геометрических характеристик сечений упругих элементов. Допускается определять момент инерции Ired без учета арматуры. В этом случае для прямоугольного сечения
. (7.19)
Значения модуля деформации бетона принимают равными при непродолжительном действии нагрузки 
; при продолжительном действии нагрузки 
, где φb,cr - принимают по табл. СП.
Жесткость изгибаемого предварительно напряженного элемента на участке с трещинами в растянутой зоне.
7.1.6. Жесткость изгибаемого предварительно напряженного элемента на участках с трещинами в растянутой зоне определяют с учетом следующих положений:
- сечения после деформирования остаются плоскими;
- напряжения в бетоне сжатой зоны определяют как для условно упругого тела;
- работу растянутого бетона в сечении с нормальной трещиной не учитывают;
- работу растянутого бетона на участке между смежными нормальными трещинами учитывают посредством коэффициента ψs.
Жесткость элемента D на участках с трещинами определяют как указано в по формуле (7.17).
Значения модуля деформации сжатого бетона Eb1 принимают равными значениям приведенного модуля деформации Eb,red, определяемым по формуле 
для соответствующих нагрузок (непродолжительного и продолжительного действия), заменяя Rb на Rb,ser.
Момент инерции приведенного поперечного сечения элемента Ired относительно его центра тяжести определяют по общим правилам сопротивления упругих элементов с учетом площади сечения бетона только сжатой зоны, площадей сечения арматуры, расположенной в сжатой зоне сечения, с коэффициентом приведения арматуры к бетону αs1 и арматуры, расположенной в растянутой зоне сечения, с коэффициентом приведения арматуры к бетону αs2: 
, где Ib, Is, I's - момент инерции площади сечения соответственно сжатой зоны бетона, арматуры, расположенной в растянутой и сжатой зоне, относительно центра тяжести приведенного без учета бетона растянутой зоны поперечного сечения.
Значения Is и I's определяют по формулам (7.18), принимая значение ус, равное расстоянию от наиболее сжатого волокна бетона до центра тяжести приведенного (с коэффициентами приведения αs1 и αs2)поперечного сечения без учета бетона растянутой зоны (рис. 7.1). Значения Ib и ус определяют по общим правилам расчета геометрических характеристик сечений упругих элементов.
Значения коэффициентов приведения арматуры к бетону αsl и αs2 определяют по формулам: для сжатой арматуры 
, длярастянутой арматуры 
; Еb,red - приведенный модуль деформации сжатого бетона, определяемый по формуле при непродолжительном и продолжительном действии нагрузки с заменой Rb на Rb,ser; Es,red - приведенный модуль деформации растянутой арматуры, определяемый с учетом влияния работы растянутого бетона между трещинами по формуле 
. Значения коэффициента ψs определяют по формуле .
Положение нейтральной оси определяют из уравнения (7.12)
Допускается для элементов прямоугольного сечения высоту сжатой зоны определять по формуле (7.13)
Кривизну изгибаемых предварительно напряженных элементов допускается определять по формуле
, (7.20)
где zp - расстояние от точки приложения усилия предварительного обжатия до точки приложения равнодействующей усилий в сжатой зоне; z - расстояние от центра тяжести растянутой арматуры до точки приложения равнодействующей усилий в сжатой зоне; xN - высота сжатой зоны с учетом влияния предварительного обжатия.
Высоту сжатой зоны определяют как для изгибаемых элементов без преднапряжения согласно СП 52-101 с умножением значения μs на 
. Значения zp и z допускается определять, принимая расстояние от точки приложения равнодействующей усилий в сжатой зоне до наиболее сжатого волокна сечения равным 0,3 h0.
8.2. Изменения в определении нагрузок согласно СП 20.13330.2011
8.2.1. Нормативное значение снеговой нагрузки на горизонтальную проекцию покрытия согласно СП следует определять по формуле
, (8.9) где 
коэффициент, учитывающий снос снега с покрытий зданий под действием ветра; 
термический коэффициент; 
коэффициент, зависящий от профиля кровли; 
расчетное значение снегового покрова на уровне, принимаемое по СП взависимости от района строительства. Вес снегового покрова Sg на 1 м2 горизонтальной поверхности земли для площадок, расположенных на высоте не более 1500 м над уровнем моря, принимается в зависимости от снегового района Российской Федерации по данным таблицы 10.1. СП 20.13330.2011 (табл. 8.1).
Таблица 8.1
| Снеговые районы (принимаются по карте 1 приложения Ж СП 20.13330.2011) | I | II | III | IV | V | VI | VII | VIII |
| Sg, кПа | 0,8 | 1,2 | 1,8 | 2,4 | 3,2 | 4,0 | 4,8 | 5,6 |
Для пологих (с уклонами до 12 % или с f/l 0,05) покрытий однопролетных и многопролетных зданий без фонарей, проектируемых в районах со средней скоростью ветра за три наиболее холодных месяца V= 2 м/с (см. схемы Г.1, Г.2, Г.5 и Г.6 приложения Г СП 20.13330.2011), следует установить коэффициент сноса снега
, (8.2) где k – принимается взависимости от высоты расчетного уровня по таблице 8.2; b – ширина покрытия, принимаемая не более 100 м.
Таблица 8.2
| Высота z, м | Коэффициент k для типов местности | ||
| А | В | С | |
| 0,75 | 0,5 | 0,4 | |
| 1,0 | 0,65 | 0,4 | |
| 1,25 | 0,85 | 0,55 | |
| 1,5 | 1,1 | 0,8 | |
| 1,7 | 1,3 | 1,0 | |
| 1,85 | 1,45 | 1,15 | |
| 2,0 | 1,6 | 1,25 | |
| 2,25 | 1,9 | 1,55 | |
| 2,45 | 2,1 | 1,8 | |
| 2,65 | 2,3 | 2,0 | |
| 2,75 | 2,5 | 2,2 | |
| 2,75 | 2,75 | 2,35 | |
| 2,75 | 2,75 | 2,75 |
Для покрытий с уклонами от 12 до 20 % однопролетных и многопролетных зданий без фонарей, проектируемых в районах с V= 4 м/с (для отдельных схем покрытия по СП 20.13330.2011) следует установить коэффициент сноса ce= 0,85.
Средняя скорость ветра V за три наиболее холодных месяца принимается по карте 2 обязательного приложения Ж СП 20.13330.2011. Снижение снеговой нагрузки не распространяется: а) на покрытия зданий в районах со среднемесячной температурой воздуха в январе выше минус 50С; б) на покрытия зданий, защищенных от прямого воздействия ветра соседними более высокими зданиями, удаленными менее чем на 10 h 1, где h 1 – разность высот соседнего и проектируемого зданий. В остальных случаях следует принимать ce = 1,0.
Термический коэффициент Ct следует применять для учета понижения снеговых нагрузок на покрытия с высоким коэффициентом теплопередачи (>1 Вт/(м2∙градС) вследствие таяния, вызванного потерей тепла. При определении снеговых нагрузок для неутепленных покрытий зданий с повышенными тепловыделениями при уклонах кровли свыше 3 % и обеспечении надлежащего отвода талой воды следует вводить термический коэффициент ct= 0,8. В остальных случаях ct = 1,0.
Коэффициент надежности по снеговой нагрузке принимается γ f =1,4.
8.2.2. Нормативное значение ветровой нагрузки w следует определять как сумму средней wm и пульсационной wр составляющих
w= wm+wp. (8.3)
Нормативное значение средней составляющей ветровой нагрузки wm в зависимости от эквивалентной высоты zе над поверхностью земли следует определять по формуле
wm=w 0 k(zе)c, (8.4) где w 0 – нормативное значение ветрового давления; k(ze) – коэффициент, учитывающий изменение ветрового давления для высоты zе; c – аэродинамический коэффициент.
Эквивалентная высота zе определяется следующим образом: а) для башенных сооружений, мачт, труб и т.п. сооружений zе=z; б) для зданий: при h≤d → zе=h; при h≤ 2 d: для z≥h–d → zе=h; для 0<z< h – d → zе=d; при h> 2 d: для z≥h–d → ze=h; для d<z<h-d → ze=z; для 0 <z≤d → ze=d. Здесь z – высота от поверхности земли; d – размер здания (без учета его стилобатной части) в направлении, перпендикулярном расчетному направлению ветра (поперечный размер); h – высота здания.
Коэффициент k(ze) определяется по таблице СП для различных типов местности: А – открытые побережья морей, озер и водохранилищ, сельские местности, в том числе с постройками высотой менее 10 м, пустыни, степи, лесостепи, тундра; В – городские территории, лесные массивы и другие местности, равномерно покрытые препятствиями высотой более 10 м; С – городские районы с плотной застройкой зданиями высотой более 25 м. Сооружение считается расположенным в местности данного типа, если эта местность сохраняется с наветренной стороны сооружения на расстоянии 30 h – при высоте сооружения h до 60 м и на расстоянии 2 км – при h > 60 м. Типы местности могут быть различными для разных расчетных направлений ветра.
Нормативное значение пульсационной составляющей ветровой нагрузки wp на эквивалентной высоте zе следует определять при расчете одноэтажных производственных зданий высотой до 36 м при отношении высоты к пролету менее 1,5, размещаемых в местностях типа А и В пульсационную составляющую ветровой нагрузки допускается определять по формуле:
, (8.5)
где wm – определяется по формуле (8.4);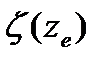 
– коэффициент пульсации давления ветра, принимаемый по таблице СП для эквивалентной высоты ze; v – коэффициент пространственной корреляции пульсаций давления ветра.
Библиографический список
1 Основная литература
1.1. Бондаренко, В.М. Железобетонные и каменные конструкции: учебник для вузов / В.М.Бондаренко [и др]; под ред.В.М.Бондаренко. – 4-е изд., доп. – М.: Высш. шк., 2007. – 887с.: ил. – Библиогр.в конце кн. – ISBN 5-06-003162-4 /в пер./: 487.90.
1.2. Заикин, А.И. Проектирование железобетонных конструкций многоэтажных промышленных зданий: (примеры расчета: учеб.пособие для вузов / А.И.Заикин. – 2-е изд.,стер. – М.: АСВ, 2005. – 200с.: ил. – Библиогр.в конце кн. – ISBN 5-93093-132-1: 125.00.
Кумпяк, О.Г. Железобетонные конструкции. Ч.1: Учебник для вузов: В 3ч. / О.Г.Кумпяк, А.М.Болдышев, Н.К.Ананьев и др.; Под ред. О.Г.Кумпяка. – М.: АСВ, 2003. – 280с.: ил. – Библиогр. в конце кн. – ISBN 5-93093-192-5 /в пер./: 120.00. – ISBN 5-93057-033-7(ч.1).
1.4. Фролов, А.К. Проектирование железобетонных, каменных и армокаменных конструкций: учеб. пособие для вузов / А.К.Фролов, [и др.]. – М.: АСВ, 2001/2002/2004. – 176с.: ил. – Библиогр. в конце кн. – ISBN 5-93093-084-8: 93.75.
1.5. Канчели, Н.В. Строительные пространственные конструкции: учеб. пособие для вузов / В.Н.Канчели. – М.: АСВ, 2003. – 112с.: ил. – Библиогр. в конце кн. – ISBN 5-93093-206-9: 125.00.
1.6. Булгаков, С.Н. Теория здания. Т.1, Здание-оболочка / С.Н. Булгаков [и др.]. – М.: АСВ, 2007. – 280с.: ил. – Библиогр. в конце гл. – ISBN 978-5-93093-518-9 /в пер./: 288.00.
2 Дополнительная литература
2.1. Алмазов, В.О. Проектирование железобетонных конструкций по евронормам / В.О.Алмазов. — М.: АСВ, 2007.— 216с.: ил. — ISBN 978-5-93093-502-8: 250.00.
Маилян, Р.Л. Строительные конструкции: учебное пособие / Р.Л.Маилян, Д.Р.Маилян, Ю.А.Веселев;под ред. Р.Л.Маиляна. – 2-е/3-е изд. – Ростов-на/Д: Феникс, 2005/2008. – 880с.: ил. – (Строительство). – Библиогр. в конце кн. – ISBN 5-222-07026-3 /в пер./: 290.00.
2.3. Бондаренко, В.М. Примеры расчета железобетонных и каменных конструкций: учеб.пособие для вузов / В.М.Бондаренко, В.И.Римшин. – 2-е изд., доп. – М.: Высш.шк., 2007. – 567с. – (Для высших учебных заведений: Строительство). – Библиогр. в конце кн. — ISBN 978-5-06-004437-9 /в пер./: 380.46.
2.4. Санжаровский, Р.С. Теория расчета строительных конструкций на устойчивость и современные нормы: Учеб. пособие для вузов / Р.С. Санжаровский, А.А.Веселов. – М.: АСВ, 2002. – 128с.: ил. – Библиогр. в конце кн. – ISBN 5-93093-146-1: 108.00.
2.5. Батищев, А.А. Современное здание. Конструкции и материалы: справочное пособие по проектированию и строительству / А.А.Батищев [и др.]. – М.-СПб.: Новое, 2004. – 704c.: ил. + 4 CD. – ISBN 5-902577-01-2 /в пер./: 1805.17. – ISBN 5-902577-02-00 (электронная версия).
2.6. СНиП II-22-81*. Каменные и армокаменные конструкции.— Взамен СНиП II-В.2-71; введ.1983-01-01.— М.: ГП ЦПП, 1996.— 40с.: ил. Интернет-ресурс.
2.7. СНиП 52-01-2003. Бетонные и железобетонные конструкции.— Взамен СНиП 2.03.01-84*; введ. 2004-03-01.— М.: ФГУП ЦПП, 2004.— 24 с.: ил. Интернет-ресурс.
Периодические издания
3.1. Бетон и железобетон. – выходит шесть раз в год.
3.2. Известия вузов. Серия Строительство. Выходит ежемесячно.
3.3. Промышленное и гражданское строительство. – выходит шесть раз в год.
3.4. Строительство и реконструкция. – выходит шесть раз в год.
3.5. Academia. Строительство и архитектура. – выходит шесть раз в год.