Задание 1 Мяч брошен с вершины скалы без начальной скорости. Найдите график зависимости модуля перемещения от времени. Сопротивлением воздуха пренебречь.

1) 1 2) 2 3) 3 4) 4
Задание 2 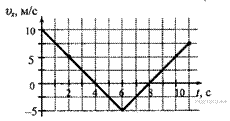 Тело движется по оси Ох. По графику зависимости проекции скорости тела vx от времени t установите, какой путь прошло тело за время от t1 = 0 до t2 = 8 с. (Ответ дайте в метрах.)
Тело движется по оси Ох. По графику зависимости проекции скорости тела vx от времени t установите, какой путь прошло тело за время от t1 = 0 до t2 = 8 с. (Ответ дайте в метрах.)
Задание 3 Тело, брошенное вертикально вверх со скоростью  , через некоторое время упало на поверхность Земли. Какой график соответствует зависимости проекции скорости на ось ОХ от времени? Ось ОХ направлена вертикально вверх.
, через некоторое время упало на поверхность Земли. Какой график соответствует зависимости проекции скорости на ось ОХ от времени? Ось ОХ направлена вертикально вверх.

1) 1 2) 2 3) 3 4) 4
Задание 4 Точечное тело движется вдоль горизонтальной оси OX. При этом его координата изменяется с течением времени t по закону x (t) = 10 + 5 t − t 2 (все величины заданы в единицах СИ). Какой из следующих графиков соответствует графику зависимости проекции скорости V этого тела на ось OX от времени?

Задание 5 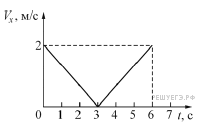 Материальная точка движется вдоль оси OX. На рисунке приведён график зависимости проекции скорости Vx этой точки на ось OX от времени t. Согласно графику, материальная точка
Материальная точка движется вдоль оси OX. На рисунке приведён график зависимости проекции скорости Vx этой точки на ось OX от времени t. Согласно графику, материальная точка
1) в момент времени t = 3 c изменила направление движения на противоположное
2) всё время двигалась в одном направлении
3) всё время имела положительную проекцию ускорения на ось OX
4) за всё время движения ни разу не останавливалась
Задание 6 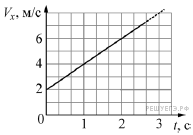 Точечное тело движется вдоль оси Оx. В начальный момент времени тело находилось в точке с координатой x = −5 м. На рисунке изображена зависимость проекции скорости Vx этого тела от времени t. Чему равна координата этого тела в момент времени t = 4 с? (Ответ дайте в метрах.)
Точечное тело движется вдоль оси Оx. В начальный момент времени тело находилось в точке с координатой x = −5 м. На рисунке изображена зависимость проекции скорости Vx этого тела от времени t. Чему равна координата этого тела в момент времени t = 4 с? (Ответ дайте в метрах.)
Задание 7 На каком из графиков изображена возможная зависимость пройденного пути от времени?
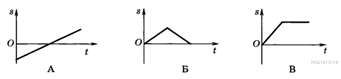
1) А 2) Б 3) В 4) Такой график отсутствует
Задание 8. Пароход движется по реке против течения со скоростью 5 м/с относительно берега. Определите скорость течения реки, если скорость парохода относительно берега при движении в обратном направлении равна 8 м/с. (Ответ дайте в метрах в секунду.)
Задание 9. 
Тела 1 и 2 двигаются вдоль оси x. На рисунке изображены графики зависимости координат движущихся тел 1 и 2 от времени t. Чему равен модуль скорости 1 относительно тела 2? (Ответ дайте в метрах в секунду.)
Задание 10  По плоскости
По плоскости  движутся четыре точечных тела —
движутся четыре точечных тела — 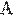 ,
,  ,
,  и
и 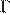 , траектории которых изображены на рисунке. Зависимости координат одного из этих тел от времени имеют вид
, траектории которых изображены на рисунке. Зависимости координат одного из этих тел от времени имеют вид  и
и 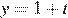 . Это тело обозначено буквой
. Это тело обозначено буквой
1) А 2) Б 3) В 4) Г
Задание 11 Два лыжника движутся по прямой лыжне: один со скоростью  , другой со скоростью
, другой со скоростью  относительно деревьев. Скорость второго лыжника относительно первого равна
относительно деревьев. Скорость второго лыжника относительно первого равна
1)  2)
2)  3)
3) 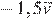 4)
4) 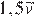
Задание 12. Тело разгоняется на прямолинейном участке пути, при этом зависимость пройденного телом пути S от времени t имеет вид:
 .
.
Чему равна скорость тела в момент времени t = 2 c при таком движении? (Ответ дайте в метрах в секунду.)
Задание 13. Тело брошено вертикально вверх. Через 0,5 с после броска его скорость 20 м/с. Какова начальная скорость тела? Сопротивлением воздуха пренебречь. (Ответ дайте в метрах в секунду.)
Задание 14. На рисунке приведен график зависимости проекции скорости тела 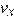 от времени.
от времени.
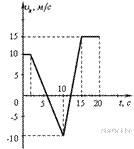
С каким из графиков совпадает график зависимости от времени проекции ускорения этого тела 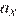 в интервале времени от 10 до 15 с?
в интервале времени от 10 до 15 с?

1) 1 2) 2 3) 3 4) 4
Задание 15. Материальная точка движется с ускорением, направление которого неизменно. Из этого следует, что скорость данной материальной точки
1) изменяется только по модулю 2) изменяется только по направлению
3) может изменяться и по модулю, и по направлению 4) не изменяется ни по модулю, ни по направлению
Задание 16 Автомобиль движется по окружности радиусом 100 м со скоростью 10 м/с. Чему равно центростремительное ускорение автомобиля? (Ответ дайте в метрах в секунду в квадрате.)
Задание 17  Бусинка может свободно скользить по неподвижной горизонтальной спице. На графике изображена зависимость ее координаты от времени. Выберите два утверждения, которые можно сделать на основании графика.
Бусинка может свободно скользить по неподвижной горизонтальной спице. На графике изображена зависимость ее координаты от времени. Выберите два утверждения, которые можно сделать на основании графика.
1) Скорость бусинки на участке 1 постоянна, а на участке 2 равна нулю.
2) Проекция ускорения бусинки на участке 1 положительна, а на участке 2 — отрицательна.
3) Участок 1 соответствует равномерному движению бусинки, а на участке 2 бусинка неподвижна.
4) Участок 1 соответствует равноускоренному движению бусинки, а на участке 2 — равномерному.
5) Проекция ускорения бусинки на участке 1 отрицательна, а на участке 2 — положительна.
Задание 18.  На рисунке приведены графики зависимости координаты от времени для двух тел: А и В, движущихся по прямой, вдоль которой направлена ось Ох. Выберите два верных утверждения о характере движения тел.
На рисунке приведены графики зависимости координаты от времени для двух тел: А и В, движущихся по прямой, вдоль которой направлена ось Ох. Выберите два верных утверждения о характере движения тел.
1) Тело А движется с постоянной скоростью, равной 5 м/с.
2) В момент времени t = 5 с скорость тела В была больше скорости тела А.
3) В течение первых пяти секунд тела двигались в одном направлении.
4) В момент времени t = 2 с тела находились на расстоянии 20 м друг от друга.
5) За первые 5 с движения тело В прошло путь 15 м.
Задание 19. Из начала декартовой системы координат в момент времени t = 0 тело (материальная точка) брошено под углом к горизонту. В таблице приведены результаты измерения координат тела x и y в зависимости от времени наблюдения. Выберите два верных утверждения на основании данных, приведённых в таблице.

1) В момент времени t = 0,4 с скорость тела равна 3 м/с.
2) Проекция скорости Vy в момент времени t = 0,2 с равна 2 м/с.
3) Тело бросили со скоростью 6 м/с.
4) Тело бросили под углом 45°.
5) Тело поднялось на максимальную высоту, равную 1,2 м.
Задание 20. На картинке приведена стробоскопическая фотография движения шарика по желобу. Промежутки времени между двумя последовательными вспышками света одинаковы. Числа на линейке обозначают длину в дециметрах. Как изменяются скорость шарика, его ускорение и сила тяжести, действующая на шарик? Начальную скорость шарика считать равной нулю.

К каждому элементу первого столбца подберите соответствующий элемент из второго и внесите в строку ответов выбранные цифры под соответствующими буквами.
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ИЗМЕНЕНИЕ ВЕЛИЧИНЫ | |
| А) Скорость шарика Б) Ускорение шарика В) Сила тяжести, действующая на шарик | 1) Увеличивается 2) Уменьшается 3) Не изменяется |
| A | Б | В |
Задание 21. Тело, брошенное с горизонтальной поверхности со скоростью  под углом
под углом 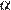 к горизонту, в течение t секунд поднимается над горизонтом, а затем снижается и падает на расстоянии S от точки броска. Сопротивление воздуха пренебрежимо мало.
к горизонту, в течение t секунд поднимается над горизонтом, а затем снижается и падает на расстоянии S от точки броска. Сопротивление воздуха пренебрежимо мало.
Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры.
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ФОРМУЛЫ | |||||
А) Время подъёма t на максимальную высоту
Б) Расстояние S от точки броска до точки падения | 1) 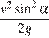 2)
2)  3)
3)  4)
4) 
|
Задание 22. Два пластилиновых шарика массами 2 m и m находятся на горизонтальном гладком столе. Первый из них движется ко второму со скоростью  , а второй покоится относительно стола. Укажите формулы, по которым можно рассчитать модули изменения скоростей шариков в результате их абсолютно неупругого удара.
, а второй покоится относительно стола. Укажите формулы, по которым можно рассчитать модули изменения скоростей шариков в результате их абсолютно неупругого удара.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ФОРМУЛЫ | |||||
А) Модуль изменения скорости первого шарика
Б) Модуль изменения скорости второго шарика | 1)  2)
2) 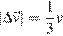 3)
3) 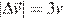 4)
4) 
|
Задание 23.  С вершины наклонной плоскости с углом наклона α = 30° горизонтально бросают точечное тело с начальной скоростью V 0 = 20 м/с.
С вершины наклонной плоскости с углом наклона α = 30° горизонтально бросают точечное тело с начальной скоростью V 0 = 20 м/с.
В системе координат, изображённой на рисунке, установите соответствие между физическими величинами, выраженными в системе единиц СИ, и их значениями. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца.
| ФИЗИЧЕСКАЯ ВЕЛИЧИНА (в СИ) | ЕЕ ЗНАЧЕНИЕ |
| А) модуль проекции ускорения на ось OY через 1 секунду после начала движения тела Б) модуль проекции скорости на ось OX через 1 секунду после начала движения тела | 1) ≈ 22,3 2) ≈ 17,3 3) ≈ 8,7 4) ≈ 10 |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| A | Б |
Задание 24.  Маленькой шайбе, покоящейся у основания гладкой наклонной плоскости, сообщают начальную скорость V 0, направленную вдоль наклонной плоскости вверх (см. рис.). Наклонная плоскость достаточно длинная. Установите соответствие между зависимостями физических величин от времени и графиками.
Маленькой шайбе, покоящейся у основания гладкой наклонной плоскости, сообщают начальную скорость V 0, направленную вдоль наклонной плоскости вверх (см. рис.). Наклонная плоскость достаточно длинная. Установите соответствие между зависимостями физических величин от времени и графиками.
| ФИЗИЧЕСКАЯ ВЕЛИЧИНА | ГРАФИК | |
| А) проекция скорости Vx Б) модуль скорости V | 
|
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Задание 25. В безветренную погоду самолет затрачивает на перелет между городами 6 часов. Если во время полета дует постоянный боковой ветер перпендикулярно линии полета, то самолет затрачивает на перелет на 9 минут больше. Найдите скорость ветра, если скорость самолета относительно воздуха постоянна и равна 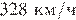 .
.
Задание 26. На рисунке представлена установка для исследования равноускоренного движения ползунка (1) массой 0,05 кг по наклонной плоскости, установленной под углом  к горизонту.
к горизонту.

В момент начала движения верхний датчик (А) включает секундомер (2), при прохождении ползунка мимо нижнего датчика (В) секундомер выключается. Числа на линейке обозначают длину в сантиметрах. Секундомер измеряет время в секундах. Скорость ползунка в любой момент времени вычисляется по формуле
1)  2)
2)  3)
3)  4)
4) 
Задание 27. Мимо остановки по прямой улице проезжает грузовик со скоростью 10 м/с. Через 5 с от остановки вдогонку грузовику отъезжает мотоциклист, движущийся с постоянным ускорением, и догоняет грузовик на расстоянии 150 м от остановки. Чему равно ускорение мотоцикла? Ответ приведите в м/с2.
Задание 28.  Тонкая палочка равномерно вращается в горизонтальной плоскости вокруг закреплённой вертикально оси OO' проходящей через точку A. Длина палочки 50 см, её угловая скорость вращения 4 рад/с, линейная скорость одного из её концов 0,5 м/с. Чему равна линейная скорость другого конца палочки? Ответ укажите в м/с с точностью до одного знака после запятой.
Тонкая палочка равномерно вращается в горизонтальной плоскости вокруг закреплённой вертикально оси OO' проходящей через точку A. Длина палочки 50 см, её угловая скорость вращения 4 рад/с, линейная скорость одного из её концов 0,5 м/с. Чему равна линейная скорость другого конца палочки? Ответ укажите в м/с с точностью до одного знака после запятой.
Задание 29. Камень, брошенный с поверхности земли почти вертикально вверх, упал со скоростью 15 м/с на крышу дома, находящуюся на высоте 20 м. Найдите время полёта камня. Сопротивление воздуха не учитывать. Ответ приведите в секундах.
Задание 30 Тело брошено под углом 60° к горизонту с плоской горизонтальной поверхности с начальной скоростью 20 м/с. Сопротивление воздуха пренебрежимо мало. На каком минимальном расстоянии от точки бросания (по горизонтали) модуль проекции скорости тела на вертикальную ось будет составлять 25% от модуля проекции скорости тела на горизонтальную ось? Ответ приведите в метрах, округлив до целого числа.