Под кинематикой жидкости понимается раздел гидромеханики, в котором изучаются кинематические характеристики движения жидкости, но не рассматриваются силы, под действием которых это движение происходит. Кинематика жидкости изучает связи между геометрическими характеристиками движения (координаты частиц, скорость, ускорение) и временем.
Жидкость представляется как сплошная легкодеформируемая среда. Ее движение представляется как движение системы неограниченного множества частиц. Причем объем каждой жидкой частицы чрезвычайно мал по сравнению с объемом жидкости, но достаточно велик по сравнению с объемом молекулы.
Установившееся и неустановившееся движение жидкости [1, С. 39], [2, С. 57–58], [3, С. 54–55]
В общем случае для потока жидкости основные характеристики потока (скорость, давление) являются функциями координат пространства и времени
 .
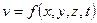| (3.1) |
Такое движение называется неустановившимся.
Примером неустановившегося движения жидкости является истечение жидкости из отверстия в резервуаре при условии, что количество воды в резервуаре не пополняется.
Если основные характеристики движения в любой точке потока не изменяются во времени, такое движение называется установившимся. Для установившегося движения можно записать
 .
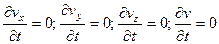| (3.2) |
Примером установившегося движения может служить истечение жидкости из отверстия в резервуаре при условии, что количество воды в резервуаре постоянно пополняется таким образом, что уровень воды в резервуаре остается постоянным.
Методы описания движения жидкости [1, С. 37–39], [2, С. 219–223], [3, С. 51–53], [4, С. 68–71]
Существует два способа математического описания движения жидкости: метод Лагранжа и метод Эйлера.
По методу Лагранжа (субстанциональный метод) рассматривается движение отдельной частицы жидкости.
Положение частицы жидкости в начальный момент времени t 0 обозначают координатами x 0, y 0, z 0. Для любой другой частицы жидкости эти координаты будут другими. При движении жидкости рассматриваемая частица перемещается, и ее координаты изменяются. Движение жидкости будет определено, если для каждой частицы будут известны координаты x, y, z как функции четырех независимых переменных: начального положения x 0, y 0, z 0 и времени t
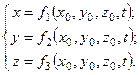
| (3.3) |
Эти уравнения характеризуют «историю» движения частиц жидкости во времени. Переменные x 0, y 0, z 0, t называются переменными Лагранжа.
Проекции скорости частицы на координатные оси определяются уравнениями
 ,
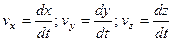| (3.4) |
а проекции ускорения
 .
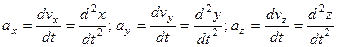| (3.5) |
Метод Лагранжа не получил в гидродинамике широкого распространения, так как он дает решение лишь для простейших случаев течения. Обычно изучение движения жидкости основывается на методе Эйлера.
Метод Эйлера (локальный метод) состоит в том, что движение всей жидкости изучается путем исследования движения в отдельных неподвижных точках, через которые протекает жидкость. Изучение движения жидкости состоит:
1) в исследовании изменений во времени векторных и скалярных величин в некоторой фиксированной точке пространства;
2) исследовании изменений этих величин при переходе от одной точки пространства к другой.
Таким образом, движение жидкости характеризуют построением поля скоростей, которое в общем случае описывается уравнениями
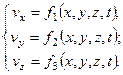
| (3.6) |
где vx, vy, vz – три взаимно-перпендикулярные составляющие полной скорости.
Таким образом, полная скорость будет равна
 .
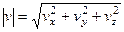| (3.7) |
Переменные x, y, z, t называются переменными Эйлера.
Для установившегося движения уравнения, описывающие поле скоростей, примут вид
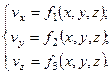
| (3.8) |
Ускорение жидкой частицы, воспользовавшись системой уравнений, описывающих поле скоростей, можно определить исходя из следующих соображений
 ,
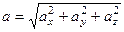| (3.9) |
где ax, ay, az – проекции ускорения на координатные оси.
Эти проекции равны
 .
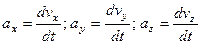| (3.10) |
В общем случае неустановившегося движения скорость является функцией координат и времени, поэтому полный дифференциал, например, скорости vx равен сумме четырех частных дифференциалов
 ,
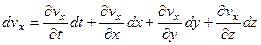| (3.11) |
а ее производная по времени
 .
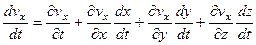| (3.12) |
Если рассматривать dx, dy, dz как проекции элементарного перемещения на оси координат, можно обозначить
| ,
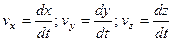| (3.13) |
Подставив эти соотношения в уравнение (3.12), и составив аналогичные выражения для производных скоростей vy и vz, можно записать систему уравнений
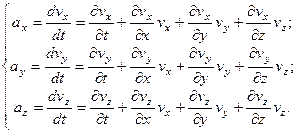
| (3.14) |
Полные производные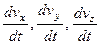 
называют проекциями субстанционального или полного ускорения. Частные производные 
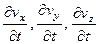называются проекциями локального (местного) ускорения. Они представляют собой интенсивность изменения составляющих скорости в данной точке (при неизменных координатах x, y, z) и обусловлены неустановившимся характером движения жидкости. При установившемся движении эти проекции равны нулю. Суммы вида 
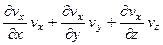и т.п. называются проекциями конвективного ускорения. Они определяют изменение той или иной составляющей скорости по координатам, т.е. при переходе из одной точки пространства в другую.
Литература.
1. Лапшев, Н.Н. Основы гидравлики и теплотехники: учебник для студ. учреждений высш. проф. образования / Н.Н. Лапшев, Ю.Н. Леонтьева. – М.: Издательский центр «Академия», 2012. – 400 с. – (Сер. Бакалавриат).
2. Гусев, А.А. Гидравлика: учебник для вузов / А.А. Гусев. – М.: Издательство Юрайт, 2013. – 285 с. – Серия: Бакалавр. Базовый курс.
3. Кудинов, В.А. Гидравлика: Учеб. пособие / В.А. Кудинов, Э.М. Карташов. – М.: Высш. шк., 2006. – 175 с.
4. Альтшуль, А.Д. Гидравлика и аэродинамика (основы механики жидкости): учебник / А.Д. Альтшуль, П.Г. Киселев. – М.: Стройиздат, 1965. – 276 с.
5. Рабинович, Е.З. Гидравлика: учеб. пособие для техникумов / Е.З. Рабинович. – 2-е изд., испр. – М.: Государственное издательство технико-теоретической литературы, 1957. – 396 с.
6. Гидравлика, пневматика и термодинамика: курс лекций / под ред. В.М. Филина. – М.: ИД «ФОРУМ»: ИНФРА-М, 2008. – 320 с. – (Профессиональное образование).
7. Кузнецов, В.А. Основы гидрогазодинамики: учебное пособие / В.А. Кузнецов. – Белгород: Изд-во БГТУ, 2012. – 108 с.