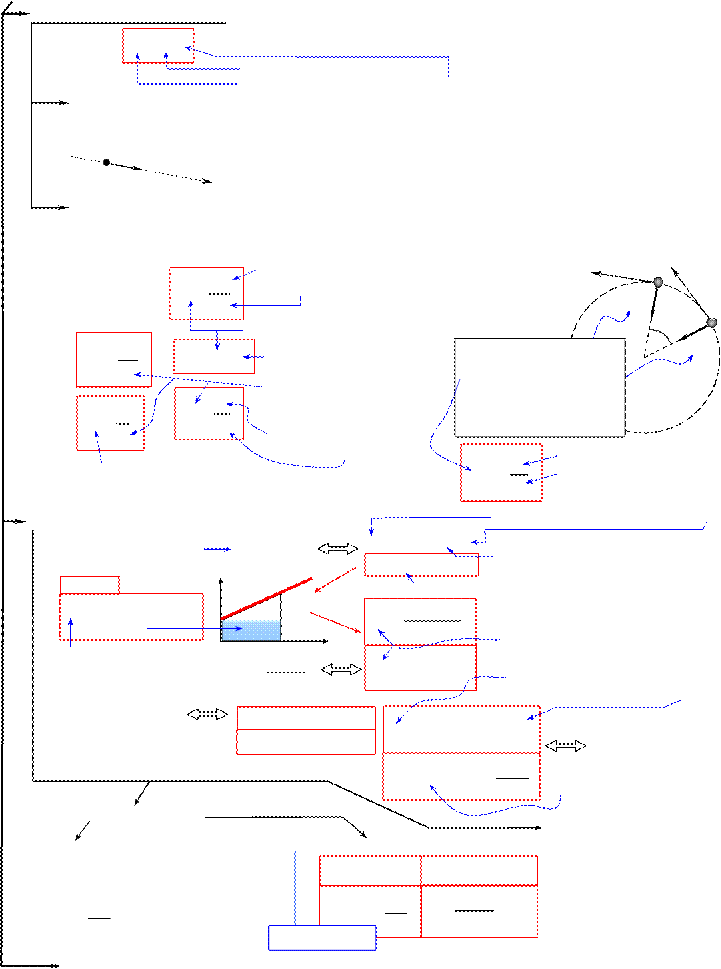
Среднее ускорение
Средний вектор скорости
(средняя скорость перемещения)
r
Средний модуль скорости
(средняя путевая скорость)
|
за время D t
v ср
=D r
D t
Вектор перемещения точки за время D t
v = s
t
Путь, пройденный за время t
t
v
2. 
Законы сложения скоростей и ускорений
t t
+ - площадь выше оси t
– - площадь ниже оси t
r r r
Скорость «подвижной» системы отсчета (ПСО) относи- r r r
vт/нсо = vт/псо + vпсо/нсо
тельно «неподвижной» (НСО) (переносная скорость)
v 1/2
= v 1
- v 2
Скорость точки (т)
относительно
«неподвижной» системы отсчета (НСО) (абсолютная скорость)
Скорость точки (т) относительно «подвижной» системы отсчета (ПСО) (относительная скорость)
Скорость первой точки относительно второй
Скорость первой точки (в «неподвижной» системе отсчета)
Скорость второй точки
(в «неподвижной»
системе отсчета)
Ускорение точки в
«неподвижной» системе отсчета (НСО) (абсолютное ускорение)
3. Нормальное и тангенциальное ускорения
Ускорение «подвижной» системы отсчета (ПСО)
относительно «неподвижной» (НСО)
(переносное ускорение)
Ускорение точки в «подвижной» системе отсчета
(ПСО)
Вектор скорости точки
|
|
составляющая полного n
ускорения, перпендикулярная вектору скорости. Это ускорение
Вектор ускорения («полное ускорение») представляют как сумму двух векторов (составляющих), один из
|
|
|
|
изменения направления вектора t r
перпендикулярен скорости:
скорости.
v 2
an =
r
|
|
Радиус кривизны траектории в той точке, где имеет место данное нормальное ускорение.
a t— тангенциальное ускорение — составляющая полного ускорения,
параллельная вектору скорости. Это ускорение характеризует быстроту изменения модуля вектора скорости:
4. Типы движений
4.1. Равномерное движение — движение, при котором точка за любые равные промежутки времени проходит
(v = const)
s = v × t
одинаковые пути (Вектор скорости не изменяется по модулю, но может меняться по
направлению)
Модуль скорости
Путь, пройденный точкой за время t
4.1.1 Равномерное прямолинейное движение — движение, при котором точка за любые равные промежутки
( v r= const )
(a = 0)
О r
v
x = x 0 + vx × t
|
времени совершает одинаковые перемещения. (Вектор скорости не меняется ни по модулю, ни по направлению)
Проекция вектора скорости на координатную ось Координата точки в начальный момент t = 0
Координата точки в момент t
4.1.2 Равномерное движение по окружности
(равномерное вращение — движение твердого тела, при котором любая его точка движется по окружности, причем, центры всех этих окружностей лежат на одной прямой перпендикулярной плоскости вращения, и за
любые равные промежутки времени тело поворачивается на одинаковые углы. ) v r
|
w=Dj
D t
Угол, на который тело поворачивается за 1 v
|
ц 1
w — Угловая скорость (измеряется в рад/с) R Djr
w=2p
T
n = 1
T
v = w × R
T = t N
R — Радиус окружности, по которой движется точка
T - Период вращения — время, за которое происходит один полный оборот.
|
|
t — время, за которое
При равномерном движении по aц
окружности точка обладает
ускорением, которое в любой момент направлено к центру этой окружности. Такое ускорение называется ЦЕНТРОСТРЕМИТЕЛЬНЫМ.
происходит N оборотов
n - частота вращения — число,
a = v
v - скорость движения точки
R – радиус окружности, по
Измеряется в герцах. 1 Гц = 1 оборот/с
которой движется точка
4.2 Движение с постоянным ускорением
vx, vy - проекции скорости в момент t
(a r= const )
D v r r r
vx = v 0 x + ax × t
При a r = const:
численно
a r =
D t
v = v 0 + at
vx
vy = v 0 y
+ ay × t
ax, ay - проекции ускорения
v 0 x, v 0 y - проекции начальной скорости
± S под = D x
граф v x (t)
D x = vx + v 0 x t
t 2
D x,
(т. е. скорости в момент t = 0)
|
+ - площадь выше оси t r r
v + v
– - площадь ниже оси t
2 a rD r r = v 2 - v 2
D r r = v + v 0 t
D y = y 0 y t
x, y – конечные координаты
(координаты в момент t)
0 2 ax ×D x = vx 2 - v x
a t 2
0 x = x 0 + v 0 x × t + x
r r r r 2
2 ay ×D y = vy 2 - v 2
2 r = r
+ v t + at
Форма траектории
при движении с постоянным ускорением:
0 y
y = y 0 + v 0 y × t +
a t 2
|
2 x 0, y 0 – начальные координаты
r r (координаты в момент t = 0)
Прямолинейная траектория (a и v
Параллельны)
Параболическая траектория
4.2.1 Равноускоренное движение a r v r
4.2.2 Равнозамедленное движение a ¯ v
v = v 0 - a × t 2 a × s = v 02 - v 2
(a rи v r не параллельны)
r
|
|
|
s = v 0 t -
= v 0/ а
at 2
s = v + v 0 t
4.3 Гармоническое движение x = A ×cos(w t + j0), vx = - A ×w×sin(w t + j0), ax = - A ×w2×cos(w t + j0)
(вдоль оси ОХ) v m = A× w a m = A× w2
x — координата колеблющегося тела (смещение от равновесного
положения); w — циклическая частота колебаний,
максимальная
скорость
максимальное ускорение
A — амплитуда колебаний (максимальное смещение)
j = w t + j0 — фаза колебаний, j0 — начальная фаза.
период колебаний (время одного полного колебания)
II. Динамика
|
m — масса материальной точки,
a — ускорение этой материальной точки,
r r r r
F 1 + F 2 + F 3 +... = F равн — сумма всех сил, действующих на эту
материальную точку (равнодействующая сила).
U U
U ИСО U — системы отсчета, относительно которых любая материальная точка, свободная от действия сил, не имеет ускорения.
Инерциальной может приближенно считаться:
· Система отсчета, связанная с поверхностью Земли (если не требуется учитывать вращение Земли и силы притяжения к Солнцу и планетам)
· Система отсчета, с центром в центре Земли, оси которой направлены на звезды (если надо учесть вращение Земли вокруг своей оси, но вращение вокруг Солнца и притяжение к Солнцу и планетам можно не учитывать).
· Система отсчета, с центром в центре Солнца, оси которой направлены на звезды (если можно не учитывать вращение солнечной системы вокруг ядра галактики и притяжение к другим звездам).
U 2. Теорема о движении центра масс
М BсистB — масса системы материальных точек (масса тела или системы тел),
|
|
U Внешние силы U — силы, действующие на тела, входящие в систему, со
r внеш
F 1
+ r внеш
+...
— сумма внешних сил,
стороны тел, не входящих в эту систему.
U 3. Третий закон Ньютона
r
действующих на эту систему.
Если одно тело (1) действует на другое тело (2) силой (F 12 ), то
второе тело (2) обязательно действует на первое (1) такой силой
r
F 21, что ®
r
F 21
"1"
"2"
r
F 12
U 4. Силы U, которые могут действовать на тело, можно разделить на две группы:
U 5. Гравитационная сила U
r r
F 21 = F 12 = F грав — сила гравитационного притяжения между двумя материальными точками или однородными шарами (сферами), массы которых m B1B и m B2B.
|
U U
g — U гравитационная постоянная U
— измеряется в специальных экспериментах, очень важная величина (фундаментальная константа)
F » F
= g M пл× m = gm
U Первая космическая скорость U —
тяж
грав.наповерхн. 2
пл
» F грав. на поверхн.
скорость спутника, который
вращается вокруг планеты по круговой орбите минимального
|
|
|
|
Вес тела — сила, с которой это тело, благодаря наличию у него массы, давит на подставку, на которой лежит, или действует на подвес, на котором висит.
Перегрузка — превышение весом величины mg. Возникает в ракетах,
лифтах и пр. при движении с ускорением, направленным вверх.
возможного радиуса r » R BплB
|
Учитывая, что r » R пB лB, получим:
v 2
m = mg Þ U
R пл
Невесомость — состояние, в котором вес равен нулю (т. е. тело не давит на подставку). Невесомость может возникать не только при отсутствии гравитационной силы, но и в лифтах, самолетах, космических кораблях и пр., движущихся с a = g.
U 6. Силы, действующие через контакт U (со стороны прикасающихся тел)
6.1. Если к телу прикасается U твердая поверхность U, то со стороны этой поверхности на тело могут действовать
две силы:
r
N - U сила
r
U Сила трения U - F тр
нормальной U
U реакции
r
N - направлена
U всегда
перпендикулярно к поверхности,
со стороны которой она действует.
Эта сила U мешает телу "пройти сквозь
r
F тр - направлена U всегда параллельно Uповерхности,
со стороны которой действует (по касательной к поверхности, если поверхность не плоская).
Эта сила U мешает телу скользить U по поверхности (иногда делает скольжение совсем невозможным).
По своей природе она является результатом взаимного притяжения молекул тела и поверхности, а также зацепления микронеровностей тела и поверхности.
Сила трения может отсутствовать: F тр
U U B B = 0, если
поверхность" U (т. е. ограничивает область
1. В задаче указано, что "поверхность гладкая".
U U
возможного движения тела).
По своей природе она является силой упругости.
Сила нормальной реакции U действует всегда U, когда между телом и поверхностью есть
2. Тело "Uне стремится скользитьU", т. е. оно не скользило бы по поверхности даже, если бы поверхность вдруг стала абсолютно гладкой и скользкой.
m - коэффициент трения m
U U
контакт.
между телом и поверхностью.
Он зависит от материала, степени шероховатости
тела и поверхности, v
а также от скорости тела
относительно поверхности v. (см. график)
6.2. 
Если к телу прикреплена U нерастяжимая натянутая нить U (трос, веревка и т. п.), то со стороны этой нити на тело действует U сила реакции нити U (сила натяжения нити)
r
T - U сила реакции нити U - направлена U всегда по нити U (или по
касательной к нити, если нить не прямолинейна).
T - сила, действующая на потолок со стороны веревки, прикрепленной к нему.
6.3. 
Если к телу прикасается
то со стороны упруго деформированного тела действует U сила упругости U (F упр) на тела, мешающие ему вернуться в недеформированное состояние. (Если мысленно рассечь деформированное тело на части, то со стороны одной части на другую тоже может действовать сила упругости.)
- длина недеформированной (свободной) пружины
l B0B
D l = l - l B0B - U удлинение U пружины
l B0B
- длина недеформированного стержня
k - коэффициент жесткости
e = =
- оU тносительное
U U
пружины
l - длина деформированной пружины
l 0 l 0
l - длина деформированного стержня
r
удлинение стержня
r
F упр
При
малых упругих деформациях
r
F 21 1 2
F 12 - сила упругости, действующая со стороны части "1" на часть "2".
сила упругости, действующая со стороны части "2" на часть "1".
S - площадь поперечного сечения
r
стержня (S ^ F упр)
s= F упр
S
- Uмеханическое
Из закона Гука:
напряжение U, возникающее в
стержне
F упр = E
S l 0
Þ F упр = D l l 0
Е - U модуль упругости U
Значит, для упругого стержня F BупрB = k ×⏐D l ⏐,
где k = ES / l B0B - коэффициент жесткости упругого стержня.
UматериалаU стержня.
III. 
|
r r r r
1. Импульс материальной точки p = m × v
2. Импульс системы материальных точек
m - масса материальной точки
r
v - скорость этой материальной точки
равен векторной сумме импульсов всех точек, входящих в эту систему.
p v
всегда!
r m
|
|
сист
p r+
p r +K+ r
Пример: импульс однородного диска, вращающегося вокруг неподвижной оси, проходящей через центр
p 3 1 r
p1
|
p диск = p 1 + p 2 + p 3 + p 4 +K+ pn = 0 m 3
3. 
|
|
|
|
- p r
p 2 m 2
- изменение импульса материальной точки.
å F - сумма всех сил, действующих на материальную точку.
r r r
Выводится из II закона Ньютона: ma = å F. Если å F = const, то a r = const и
r D v r v r - v r
D t - время действия сил.
r
F × D t - импульс силы.
a = = 2 1
D t D t
Подставив в уравнение и, домножив обе части на D t, получим …
4. Теорема об изменении импульса системы материальных точек
r r r r r
r r r r
Из п. 2: D p сист = D p 1 +D p 2 +K+D pn =å F D t;
r
å F = å F
внеш
+ å F
внутр
= å F
+ 0
внеш
kå F — сумма всех сил, действующих на все мат. точки системы
r r r r r
Из п.3: D p 1 = å F 1D t, D p 2 = å F 2D t, …
å F внеш — сумма внешних сил, действующих на все мат. точки системы
r
å F внутр — сумма внутренних сил, действующих на все мат. точки системы
r r r r r r r r r r r
|
D p r
сист
r
|
å F внеш
— сумма внешних сил, действующих на все мат. точки системы
|
F = const
внеш
D t — время, в течение которого действовали силы.
r
5.
|
D p сист
— изменение импульса системы материальных точек за время D t
6. Работа силы
Единица измерения
A r — работа силы r О Х
|
|
|
1Дж = 1Н×м
А > 0, если a — острый угол. r r F
r
F
a
D r r
D r — перемещение материальной точки, на
r
которую действует сила F.
|
А < 0, если a — тупой угол. F D r
r
Чтобы найти работу не постоянной силы над точкой, которая движется по произвольной
a о r r
А = 0, если r = 90. F r
D r r
траектории, надо мысленно разбить движение на такие малые перемещения dr, dr, K,
1 2
r F 2 D r
чтобы на каждом из них с достаточной точностью можно было бы считать движение
F 1 dr r
r r r r
прямолинейным, а силу постоянной. Тогда
A = F 1 dr 1 + F 2 dr 2 +K
7. Мощность
Единица измерения мощности в СИ
Работа, совершенная за время t.
|
r
F
a v r
1 Вт = 1Дж/с
средняя мощность: мгновенная мощность:
|
|
8. Механическая энергия
N = Fd
dt
= F × v
Е мех = Е к + Е р
Кинетическая энергия
Этой энергией обладают движущиеся тела.
Потенциальная энергия — этой энергией обладают тела, на которые
действуют консервативные силы: F грав (F тяж), F упр, F электр
Консервативны, если они неизменны во времени для каждого положения, или являются внутренними для системы.
Силы, работа которых над системой при ее перемещении зависит только от начального и конечного положений этой системы. Работа консервативных сил не зависит от того, каким способом (по какой траектории) система была
mv 2
E =
сист
|
= Ek 1 + Ek 2 +K
переведена из начального положения в конечное.
k 2 Кинетическая энергия системы
материальных точек.
Основное свойство консервативных сил: работа консервативных сил над системой, совершившей движение по замкнутой траектории
Кинетическая энергия
материальной точки массой m, движущейся со скоростью v.
Теорема о кинетической
(когда конечное положение совпадает с начальным), равна нулю.
Потенциальная энергия — это такая функция от расположения системы, убыль которой при перемещении системы равна работе
энергии:
D Ek = A всех сил
Работа всех сил, действующих в системе.
консервативных сил на этом перемещении.
|
Изменение
кинетической энергии системы
9. Теорема о механической энергии
положении "М" потенциальная энергия системы Ер (М) = А конс М–О
Ер (тяж) = ± mgh центра масс над нулевым уровнем
|
=D Ek +D Ep = A всех сил - A конс = A неконс. сил
|
|
10. 
|
E м′ех
= E м′ех
Если А неконс = 0
11. Диссипативные силы — неконсервативные силы, работа которых сопровождается выделением
F трения скольжения; F сопр. жидк. и г.; F неупруг. взаимод. тепла.
А внутр. дис = – Q — не зависит от системы отсчета
12. 
Методы вычисления работы
E ¢мех – E ²мех = Q
Если А неконс = А внутр. дис.
13. Средняя по времени сила
|
|
|
|
D r r
× cos a
r
F = const
r
F ср
D p r
= сист
D t
|
A упр =
|
Средняя по времени сумма внешних сил, действующих на систему материальных точек
Изменение импульса системы за
время D t
|
r
|
|
|
F под графиком Fx (x)
Численно
"+" - если график выше оси x x
"-" - если график ниже оси x