1 Вб = 1Тл×м2
Отталкиваются
B n
a 7. Явление самоиндукции — возникновение ЭДС
S в контуре вследствие
|
|
Fсобст = LI
изменения собственного магнитного потока через
õ i = v×l × B
l v e
r
B
v Û
r
F лор
Индуктивность контура – коэффициент
õ пропорциональности между силой тока в контуре и собственным магнитным потоком.
этот контур.
|
LI 2
W =
õсам
=- L D I
õсам
= - L dI
dt
= - LI ¢(t)
магнитным полем, которое породил ток,
кат 2
Если I меняется равномерно
ЭДС самоиндукции
текущий в контуре.
IX. Колебания и волны
1. Колебаниями называется точное или приближенное повторение какого-либо процесса с течением времени
(обычно повторение бывает многократным).
В зависимости от физической природы повторяющегося процесса различают:
а) Механические колебания — повторяющийся процесс представляет собой механическое
движение: б) Электромагнитные колебания — повторяющийся процесс представляет собой
r
изменение силы тока, напряжения, заряда конденсатора в электрической цепи, вектора E
r
электрического поля), вектора B (индукции магнитного поля).
(напряженности
в) Другие колебания — повторяться могут и другие процессы, например, изменение температуры и пр.
Колеблющимися величинами называются физические величины, описывающие процесс, повторяющийся при колебаниях, (или систему, с которой этот процесс происходит) и сами испытывающие повторяющиеся изменения.
В механических колебаниях колеблющимися величинами могут быть: координата, скорость, ускорение и другие величины,
описывающие механическое движение.
В электромагнитных колебаниях колеблющимися величинами могут быть: сила тока, напряжение, заряд конденсатора,
r r
поле.
E, B и другие величины, описывающие электрический ток и электромагнитное
Периодическими называются колебания, при которых происходит точное повторение процесса через равные промежутки времени.
Периодом периодических колебаний называется минимальное время, через которое система возвращается в первоначальное
состояние и начинается повторение процесса.
Процесс, происходящий за один период колебаний, называется «одно полное колебание».
Частотой периодических колебаний называется число полных колебаний за единицу времени (1 секунду) — это может быть не целое число.
x — колеблющаяся величина (например, сила тока в цепи,
или координата точки)
t — время
Т — период колебаний
n = 1
T
Период — время одного полного колебания.
Чтобы вычислить частоту n, надо разделить 1 секунду на время Т одного колебания (в секундах) и получится число колебаний за 1 секунду.
2. Гармоническими колебаниями называются колебания, в которых колеблющиеся величины зависят от времени
по закону синуса, или косинуса.
Колеблющаяся величина (координата точки, сила тока, напряженность поля, или иная величина)
x = A ×cos(w t + j0)
Начальная фаза — значение фазы j в
момент t = 0. Изменяя значение j0, можно получать различные значения x в момент t = 0.
Амплитуда колебаний — максимальное отклонение
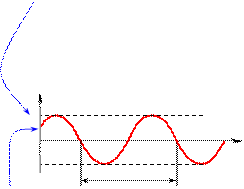колеблющейся величины от среднего за период значения.
Если среднее за период значение колеблющейся величины равно 0, то амплитуда равна максимальному значению колеблющейся величины: А = хm
x — колеблющаяся величина
А
t — время
Фаза колебаний — аргумент функции синус или косинус в уравнении зависимости колеблющейся величины от времени.
j = w t + j0
Циклическая частота колебаний — скорость изменения
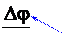фазы с течением времени.
|
-А
Значение х в момент t = 0 определяется
Т — период колебаний
Если время D t равно периоду колебаний Т, то изменение фазы Dj за это время (Т) должно быть равно 2p (т. к. функции sin и cos повторяют свои значения при изменении аргумента (j) на 2p, а через время T значение колеблющейся величины как раз должно повториться).
Таким образом, при D t = Т будет Dj= 2p Þw = Dj= 2p
величиной j.
Если колебания гармонические,
т. е. колеблющаяся величина x равна x = A ×cos(w t + j0),
то вторая производная колеблющейся величины по времени x ¢¢
D t T
подставлено 1/ Т = n
будет пропорциональна самой колеблющейся величине (x):
x ¢(t) = -w A ×sin(w t + j0)
Если x — координата точки, движущейся вдоль оси ОХ, то:
x ¢(t) = vx — проекция скорости Þ v max = w A — максимальная
скорость.
|
x ¢¢(t) = ax
— проекция ускорения Þ a
max
= w2 A - максимальное
ускорение.
Это уравнение называется дифференциальным уравнением гармонических колебаний. Если какая-либо физическая величина х подчиняется уравнению такого вида, то можно утверждать, что она зависит от времени по гармоническому закону (sin и cos), а процесс, который описывает величина х, представляет собой гармонические колебания.
3. 
Простейшие колебательные системы
Пружинный маятник
k
Математический маятник
Колебательный контур
m m
T = 2p
k T = 2p l l
T = 2p LC
Период свободных
колебаний
k
Жесткость пружины
Масса колеблю- щегося груза
m
Период
свободных колебаний
Длина
g нити
Ускорение свободного
падения — ускорение, создаваемое
Период свободных L
электромагнитных С
колебаний
ИндуктивностьЭлектроемкость
в отсутствие трения
силой тяжести.
катушки
эл
магн
конденсатора
|
kx 2
mv 2
kA 2
mv 2
Если кроме силы тяжести на маятник действуют
W конд + W кат
= const 2 C
+ 
= const =
2 2
= max
2 2
другие постоянные активные силы, то вместо g в
формулу подставляют модуль ускорения, создаваемого суммой всех активных сил:
r
CU 2
+ LI
CU 2
= const = max
LI 2
= max
x = D l — удлинение пружины
r å F акт
2 U - напряжение на конденсаторе q - его заряд
А = x max = D l max — амплитуда колебаний
a акт =
m
(активными называются
q
I – сила тока в катушке,
(максимальное удлинение пружины)
v max — максимальная скорость груза
vx = x¢ (t) = xm w×sinw t
силы, имеющие ненулевой вращающий момент относительно точки подвеса маятника)
T = 2p l a акт
2 C q max, U max и I max – максимальные (ампли-
тудные) значения заряда, напряжения и силы
тока.
I = -q¢ (t) = qm w×sinw t
xm w = v max
T
- v max 4
T 3 T
2 4 T t
Маятник в лифте:
r r
qm w = I max
T
- I max 4
T 3 T
2 4 T t
A = x max
x = xm ×cosw t
t
a лифта
l
a лифта
l
q max
q = qm ×cosw t
T
2 t
-x max
TT 3 T T
4 2 4
T = 2p
r
g + a
лиф
T = 2p
r
g - a
лиф
T
-q max 4
3 T T
|
|
4. Волна — распространение колебательного процесса в пространстве с течением времени. (Если в какой-то области пространства происходит колебательный процесс, то это может породить аналогичные колебания в соседних областях пространства.
Например, если какая-либо точка упругой среды совершает механические колебания, то при этом она, как правило, заставляет колебаться
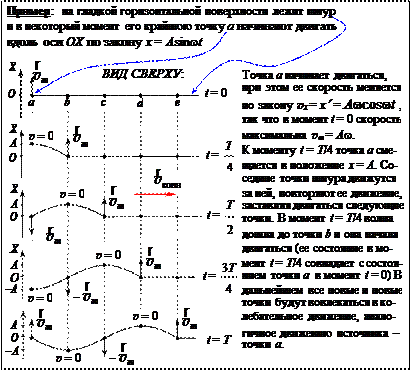соседние, прилегающие к ней точки среды. Те, в свою очередь, передают колебательное движение следующим точкам и т. д. Таким образом, в колебательный процесс вовлекаются все новые и новые области пространства. Другой пример – электромагнитные колебания. Если в какой-то точке пространства (эту точку назовем источником) происходят
r
колебания индукции магнитного поля B, то это порождает в
окружающем пространстве колебания напряженности
r
электрического поля E, которые, в свою очередь, порождают
r
новые колебания B и т. д. Электромагнитные колебания
распространяются от источника, т. е. начинают происходить во все новых и новых областях пространства)
Фронт волны — поверхность отделяющая область пространства, в которой уже начались колебания, от области, где колебания еще не происходят. Фронт волны перемещается по мере распространения волны. (В рассмотренном примере со шнуром фронтом волны в момент
t = Т /4 является точка b, в момент t = Т /2 – точка с, и т. д.)
r
Скорость распространения волны ( v волн ) — скорость
движения волнового фронта, а также любой другой поверхности постоянной фазы (любого «горба» волны, или «впадины»).
Механическая волна называется поперечной, если направление движения колеблющихся точек в ней
r r
перпендикулярно направлению v волн. Если же колеблющиеся точки движутся параллельно v волн, то волна называется продольной.
(Рассмотренная в примере волна в шнуре – поперечная, а звук – продольная волна.) Электромагнитные волны являются поперечными, т. к.
r r
|
х
колеблющаяся величина
r
|
l
кулярно r.
r – расстояние до источника
X. Оптика
1. Закон отражения Луч падающий и луч отраженный лежат в одной плоскости с нормалью, проведенной к отражающей поверхности в точке падения луча. При этом угол падения равен углу отражения.
Нормаль (перпендикуляр)
к отражающей поверхности
|
a b
Плоское зеркало
S
S S¢ — изображение светящейся точки S в
плоском зеркале — точка пересечения продолжений всех лучей, отраженных от зеркала — наблюдателю кажется, что лучи, попадающие в его глаз,
SО = ОS¢
О S¢
В¢ А ¢
Падающий луч
Отраженный луч
Глаз наблюдателя
приходят из точки S¢ В
Изображение точки в плоском зеркале лежит на перпендикуляре, проведенном к зеркалу из этой точки, причем,
расстояния до зеркала от точки и от ее изображения одинаковы. А
2. Закон преломления
Изображение предмета симметрично самому предмету относительно плоскости зеркала
При переходе из одной прозрачной среды в другую световой луч частично отражается от границы раздела сред, а частично проходит в следующую среду, причем, в новой среде направление луча может измениться. Такой луч, изменивший свое направление при переходе в новую среду, называется ПРЕЛОМЛЕННЫМ лучом. Луч падающий и луч преломленный лежат в одной плоскости с нормалью,
Угол падения
Нормаль (перпендикуляр)
проведенной к границе раздела сред в точке падения луча. При этом
⎛ sin a ⎞
к границе раздела сред
отношение синуса угла падения к синусу угла преломления ⎜ ⎟
a
a
Падающий
Отраженный луч
есть величина постоянная для данных двух сред при данной частоте излучения.
абсолютный показатель
⎝sin b ⎠
луч
(результат
sin a
v n преломления второй среды
|
|
= света 1 = 2
абсолютный показатель
отражения)
Преломленный луч
Sin b
света 2 1
преломления первой среды
Абсолютный показатель преломления – показатель
b
n 2 > n 1; a > b
Угол преломления
n 2 < n 1; a < b
Относительный
показатель преломления (показатель преломления второй среды относительно первой)
При переходе луча
Отношение скорости
света в первой среде к скорости света во второй
преломления среды относительно
вакуума: с
n среды =
v света в среде
|
a (стекло)
n 1
в оптически менее плотную среду (n 2 < n 1) может произойти ПОЛНОЕ ОТРАЖЕНИЕ луча от границы раздела сред, если угол
Скорость света в вакууме с » 3×108 м/с
v света в воздухе » с, т. е. n воздуха »1
n 2 b
падения слишком велик: a≥ a0 a0 - угол полного внутреннего отражения
|
|
Среда 2
Среда 2 (воздух) n 2 < n 1 Þ a < b
угол преломления b0 = 90о Þ
b
При переходе луча в оптически более
(воздух)
При переходе луча в оптически менее
b0= 90о
a0
a > a0
sin a0 =
плотную среду
(n 2 > n 1)
плотную среду
(n 2 < n 1)
n 1 Среда 1 (вода)
n
если луч выходит в
луч приближается к луч отдаляется от
нормали нормали
n 1×sin a1 = n 2×sin a2 = … = const
При углах падения меньших, чем a0, луч отражается от границы раздела сред лишь частично (с ростом a доля отраженной энергии растет)
При a ≥ a0 луч полностью отражается от границы раздела сред и не выходит во вторую среду
воздух или вакуум из среды с показателем преломления n
R 2 и R 1 берутся со
произведение показателя преломления среды на синус угла между лучом и нормалью в этой среде
остается неизменным при переходе из одной среды в другую
R 2
4. Линза — прозрачное тело, ограниченное двумя сферическими поверхностями.
знаком «+», если сфера выпуклая,
«-» - если вогнутая
Линза считается тонкой, если ее толщина АВ мала по сравнению с радиусами R 1 и R 2 сферических поверхностей, ограничивающих линзу, а также по сравнению с расстояниями d и f от линзы до
предмета и от линзы до изображения.
А В О 1
О 2
Линза называется собирающей, если лучи, падающие на нее параллельно друг другу, после преломления сходятся.
Главная оптическая ось линзы – прямая, R 1
проходящая через центры О 1 и О 2 сферических
поверхностей, ограничивающих линзу.
Линза называется рассеивающей, если лучи, падающие на нее параллельно друг другу, после преломления расходятся.
Обозначение тонкой собира- ющей линзы
Обозначение тонкой рассеива- ющей линзы
Фокусом линзы называется точка, в которой после преломления
Фокус линзы
пересекаются лучи, упавшие на линзу параллельно ее главной
O F
оптической оси (или продолжения преломленных лучей, если
линза рассеивающая).
Оптическая сила линзы
⎛ ⎞ ⎛ ⎞
|
Фокусное расстояние
линзы – расстояние от
измеряется в диоптриях:
D = F = ⎜ n - 1⎟× ⎜⎜ ± R + ± R ⎟⎟
F > 0 F
линзы до фокуса.
⎜ ⎜ F < 0
1 дптр = 1/м = 1м-1
⎝ среды
⎠⎝ 1 2 ⎠
F
В СИ измеряется в метрах.
5. 
Изображение точки S в линзе – это такая точка S ¢, в которой лучи, вышедшие из точки S, пересекаются после преломления в линзе.
Чтобы построить изображение S ¢ точки S, надо знать ход двух лучей,
S
h O F A ¢
вышедших из S и преломленных в линзе (где пересекутся эти лучи, там пересекутся и все остальные). Всегда известен ход следующих лучей:
· луч, падающий на линзу параллельно главной оптической оси,
A F
размер предмета
Н – размер
изобра-
S¢ жения
преломившись, проходит через фокус (если линза собирающая) или идет так, что его продолжение проходит через фокус (если линза рассеивающая)
· луч, падающий на собирающую линзу, по прямой, проходящей через фокус, (луч, падающий на рассеивающую линзу вдоль прямой, проходящей через фокус, расположенный с другой стороны линзы) преломившись, идет
расстояние
⎜ d ⎜ ⎜ f ⎜
расстояние
параллельно главной оптической оси
от линзы до предмета
от линзы до изображения
· луч, проходящий через оптический центр тонкой линзы, после преломления
практически не отклоняется от прямой, вдоль которой он упал на линзу.
1 + 1 = 1
± d ± f ± F
Если показатель преломления среды одинаков с обеих сторон линзы, то оптический центр (точка О на рисунке) – пересечение главной оптической оси с плоскостью тонкой линзы.
Формула тонкой линзы Расстановка знаков в
Линейное (поперечное) увеличение — отношение размера изображения (H) к размеру предмета (h),
когда предмет — отрезок, перпендикулярный главной оптической оси.
формуле тонкой линзы: Перед фокусным расстоянием ⎜ F ⎜: «+» — если линза собирающая, « - » — если линза рассеивающая.
S¢
Перед расстоянием ⎜ f ⎜ от линзы до изображения: «+» — если изображение действительное, т. е. лучи от S
точечного источника после преломления в линзе сходятся:
« - » — если изображение мнимое, т. е. лучи от точечного источника
S ¢ S
f > 0
его нельзя получить
на экране, как действительное изображение
после преломления в линзе расходятся. В этом случае изображением считается точка пересечения продолжений преломленных лучей S ¢ (именно
в этой точке видится источник света глазу, в который попадают преломленные лучи)
f < 0
глаз видит мнимое изображение S¢
Перед расстоянием ⎜ d ⎜ от линзы до предмета: «+» — если предмет действительный, т. е. лучи от точечного
источника падают на линзу расходящимся конусом:
« - » — если предмет мнимый, т. е. лучи от точечного источника
S
d > 0
падают на линзу сходящимся конусом (это возможно, например,
если лучи предварительно прошли через собирающую линзу).
В этом случае предметом считается точка пересечения продолжений лучей, упавших на линзу.
6. 
Возможные случаи расположения предмета:
S
d < 0
S
мнимый предмет
6.1. d ® ¥ (т. е. d >> ⎜ F ⎜) В этом случае лучи от точечного источника идут практически параллельно друг другу. F
f = F — изображение точечного источника находится в фокальной плоскости. S¢
6.2. d Î (2 F; ¥ )
Изображение:
6.3. d = 2 F; f = 2 F …
f Î (F; 2 F) F 2 F
действительное (f > 0),
d ® ¥
f = F
(фотография) 2 F F
перевернутое,
уменьшенное (| d | > | f | Þ G < 1)
F 2 F
6.4. d Î (F; 2 F)
F 2 F
Изображение: действительное (f > 0),
2 F F
Размер изображение равен
размеру предмета (d = f, G = 1)
S
f Î (2 F; ¥ )
2 F F
перевернутое,
6.5. d = F; f ® ¥ - лучи от источника, F
(кино,
диафильм)
увеличенное (| d | < | f | Þ G > 1)
лежащего в фокальной плоскости, преломившись, идут параллельно. F
6.6. d Î (0; F)
Изображение:
6.7. Рассеивающая линза:
Для собирающей
f Î ( - ¥ ; 0)
(лупа) F
мнимое (f < 0),
F прямое,
увеличенное (| d | < | f | Þ G > 1)
Изображение:
мнимое (f < 0),
прямое,
линзы:
F
f
перевернутое
уменьшенное (| d | > | f | Þ G < 1)
7. Интерференция — наложение волн, при котором эти волны в одних точках усиливают друг друга,
а в других — ослабляют друг друга, так, что интенсивность результирующей волны не равна сумме интенсивностей складывающихся волн (I ¹ I 1 + I 2) Наблюдать интерференцию можно только при наложении когерентных волн.
2 F F
d
F 2 F
прямое
Когерентными называются волны, разность фаз (j2 – j1) которых в точке наложения не меняется с течением времени.
Фаза гармонической (монохроматической) волны: j=w t - 2p r
+ j. Для когерентных волн:
оптическая разность хода
Чтобы волны были когерентны, необходимо: w1 = w2 r
lвак
-
опт
длина
волн от источника до
точки наложения
опт оптическая
d S 2
r 2 M
x
точка наложения волн от источников S 1 и S 2
пути волны от источника до точки наложения волн: r опт = r 1 n 1 + r 2 n 2 + …
Длина накладывающихся световых волн в вакууме
Dопт = r 1опт – r 2опт
m = 1, 2, 3, …
r 1
S 1
L
О Разность хода этих волн: D= r 1 – r 2 = d × x / L
Ширина интерференционной полосы: h = l× L / d
(расстояние между соседними максимумами)
Условие максимума:
Условие минимума:
номер (порядок)
интерференцион- ного минимума
8. Дифракция — отклонение от прямолинейного распространения волн при огибании препятствий (прохождении
m = 0, 1, 2, 3, …если j02 = j01
номер (порядок) интерференционного максимума
лазер максимумы
d ×sin a k = k ×l
отверстий). В результате дифракции света возникает картина
чередования светлых и темных полос, причем свет может
попасть в зону геометрической тени. Дифракционная решетка -
a2 a1
a2 a1
первого порядка (k = 1) центральный максимум (k = 0) максимумы
период решетки
d = (10-3/ N) м
пластинка с чередующимися прозрачными и непрозрачными полосками (~ 102 на 1 мм)
второго порядка (k = 2)
число штрихов
на 1 мм