Учебно-исследовательская работа
по дисциплине
Эконометрическая модель национальной экономики Германии
Москва
Общая характеристика экономики Германии
ФРГ – одна из крупнейших стран Западной Европы (после Франции и Испании). Берлин – столица и резиденция правительства; некоторые министерства расположены в Бонне. Форма правления – парламентская республика, форма государственного устройства – симметричная федерация. Государство состоит из 16 частично независимых земель.
Германия является членом Европейского союза, принимает активное участие в НАТО, а также входит в «Большую восьмёрку».
По уровню экономического развития, величине экономического потенциала, доле в мировом производстве, степени вовлеченности в международное разделение труда и другим важнейшим критериям она относится к числу наиболее высокоразвитых государств мира. По объему ВВП она занимает пятое место в мире. По уровню жизни – 18 место в мире, согласно Human Development Index. Она мало уступает США – крупнейшей торговой державе мира – по объему внешней торговли, хотя ее экономический потенциал почти втрое меньше. Она является также одним из крупнейших экспортеров и импортеров капитала. По качественным характеристикам национальной экономики (уровень производительности труда, капиталооснащенность и наукоемкость производства и др.) страна также занимает одно из первых мест в мировом хозяйстве.
С точки зрения обеспеченности природными ресурсами ФРГ нельзя отнести к числу богатых стран. Она располагает немногими видами топлива и сырья. К их числу относятся каменный и бурый уголь, калийная соль, небольшие запасы железной руды, легирующих и цветных металлов. Подавляющая часть топлива – нефти и газа, а также атомного сырья ввозится из-за рубежа.
|
|
Внешняя торговля – одна из наиболее динамичных отраслей экономики ФРГ, стимулятор ее экономического роста. В послевоенный период происходил постоянный рост доли экспорта в ВНП (1950 – 9,3%; 1980 – 26,7%; 1991 – 32,8%). К слабым сторонам экономического развития Германии можно отнести следующее: заниженная оценка затрат на модернизацию Восточной Германии, дефицит специалистов (необходимость их привлечения из-за рубежа); старение населения, стабильный уровень безработицы (11%), острая конкуренция со стороны быстро развивающихся стран Азии.
Идентификация модели методом двухшагового МНК
Задачей исследования является идентификация двухшаговым методом наименьших квадратов упрощенной модели Клейна (т.е. нахождение оценок коэффициентов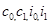 
):
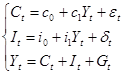(1)
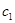– склонность к потреблению,
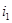– склонность к инвестированию,
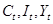- эндогенные переменные модели, 
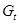- экзогенная переменная модели, 
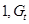– предопределенные переменные. Лаговых эндогенных переменных в модели нет.
Идентификация модели состоит в нахождении по исходным данным оценок коэффициентов модели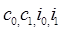 
(а также дисперсий случайных составляющих 
, 
)
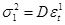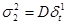На первом шаге установим регрессионную зависимость эндогенных переменных (C, I) от предопределенных переменных. Предварительно необходимо преобразовать модель от расширенной формы к структурной (2), а затем к приведенной (3):
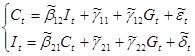(2)
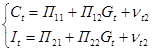(3)
Используя инструмент «Регрессия» пакета «Анализ данных» проведем парную регрессию потребления и инвестиций по государственным расходам (т.е. эндогенных переменных по предопределенным) и найдем МНК-оценки коэффициентов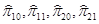 
приведенной формы.
|
|
| ВЫВОД ИТОГОВ | ||||||||
| Регрессионная статистика | ||||||||
| Множественный R | 0,98 | |||||||
| R‑квадрат | 0,96 | |||||||
| Нормированный R‑квадрат | 0,96 | |||||||
| Стандартная ошибка | 38,37 | |||||||
| Наблюдения | ||||||||
| Дисперсионный анализ | ||||||||
| df | SS | MS | F | Значимость F | ||||
| Регрессия | 1 205 387,78 | 1 205 387,78 | 818,94 | 2,334E‑26 | ||||
| Остаток | 52 987,74 | 1 471,88 | ||||||
| Итого | 1 258 375,52 | |||||||
| Коэффициенты | Стандартная ошибка | t‑статистика | P‑Значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% | |
| Y‑пересечение | -161,88 | 33,83 | -4,79 | 0,00 | -230,49 | -93,27 | -230,49 | -93,27 |
| G | 3,46 | 0,12 | 28,62 | 0,00 | 3,22 | 3,71 | 3,22 | 3,71 |
Таким образом, имеем 
| Регрессионная статистика | ||||||||
| Множественный R | 0,90 | |||||||
| R‑квадрат | 0,81 | |||||||
| Нормированный R‑квадрат | 0,80 | |||||||
| Стандартная ошибка | 40,61 | |||||||
| Наблюдения | ||||||||
| Дисперсионный анализ | ||||||||
| df | SS | MS | F | Значимость F | ||||
| Регрессия | 251965,2 | 251965,2 | 152,8 | 1,621E‑14 | ||||
| Остаток | 59366,3 | 1649,1 | ||||||
| Итого | 311331,4 | |||||||
| Коэффициенты | Стандартная ошибка | t‑статистика | P‑Значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% | |
| Y‑пересечение | -138,86 | 35,81 | -3,88 | 0,000429971 | -211,48 | -66,23 | -211,48 | -66,23 |
| G | 1,58 | 0,13 | 12,36 | 1,62091E‑14 | 1,32 | 1,84 | 1,32 | 1,84 |
|
|
.
Вычислим также выровненные значения Ĉ и Î. (Приложение 2)
На втором шаге запишем уравнения в стандартном виде, т.е. по одной эндогенной переменной в левой части с коэффициентом 1. Эндогенные же переменные в правых частях заменим на их выровненные значения.
Рассмотрим второй шаг применительно к первому уравнению, для этого в него вместо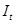 
подставим 
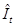, тогда получим
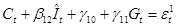
или
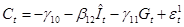
Т.к. согласно первоначальной модели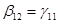 
, последнее уравнение запишется как модель парной регрессии
,
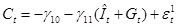в которой зависимой переменной служит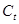 
, а независимой – 
.
МНК-оценки параметров этой модели имеют вид
.
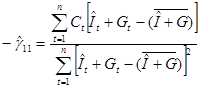
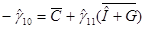Подставив в последние формулы значения временных рядов 
, 
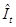и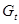 
получим
.
.
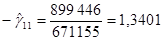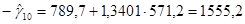Подставляя эти значения в формулы, имеем:
.
.
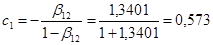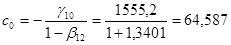Таким образом, применение двухшагового МНК к первому уравнению структурной формы позволило идентифицировать первое уравнение первоначальной формы: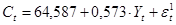 
.
Рассмотрим второй шаг для второго уравнения, для этого в него вместо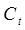 
подставим 
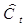, тогда получим:
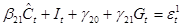
Или
.
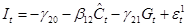Поскольку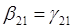 
, то последнее уравнение запишется как модель парной регрессии:
,
в которой зависимой переменной служит 
, а регрессором выступает – (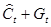
), поэтому МНК – оценки параметров этой модели имеют вид:
Подставив в последние формулы значения временных рядов 
, получим:
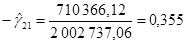
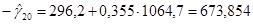
Подставляя эти значения в формулы:
.
.
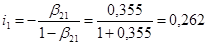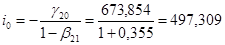Таким образом, применение двухшагового МНК ко второму уравнению структурной формы позволило идентифицировать второе уравнение первоначальной формы: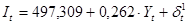 
.
Найдем оценки дисперсий случайных составляющих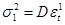 
, 
.
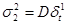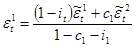
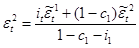
Для этого решим систему уравнений, подставив в левую часть квадрат стандартной ошибки для регрессий потребления по государственным расходам, а также чистых инвестиций по государственным расходам:
Таким образом, по итогам двухшагового МНК эконометрическая модель имеет вид:
